Gegeben ist die Funktion \(f \colon x \mapsto 3x + 2 + \dfrac{1}{x^{2}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Untersuchen Sie das Symmetrieverhalten von \(G_{f}\) bzgl. des Koordinatensystems.
b) Geben Sie die Art und die Gleichungen aller Asymptoten der Funktion \(f\) an.
c) Geben Sie eine Stammfunktion der Funktion \(f\) an.
\[f(x) = 3x + 2 + \frac{1}{x^{2}}\]
Symmetrieverhalten von \(G_{f}\) bzgl. des Koordinatensystems
Man bestimmt den Funktionsterm \(f(-x)\). Gilt \(f(-x) = f(x)\), ist \(G_{f}\) achsensymmetrisch zur \(y\)-Achse. Gilt \(f(-x) = -f(x)\), ist \(G_{f}\) punktsymmetrisch zum Koordinatenursprung \(O(0|0)\). Trifft keiner der beiden Fälle zu, weist \(G_{f}\) keines der beiden Symmetrieverhalten auf.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
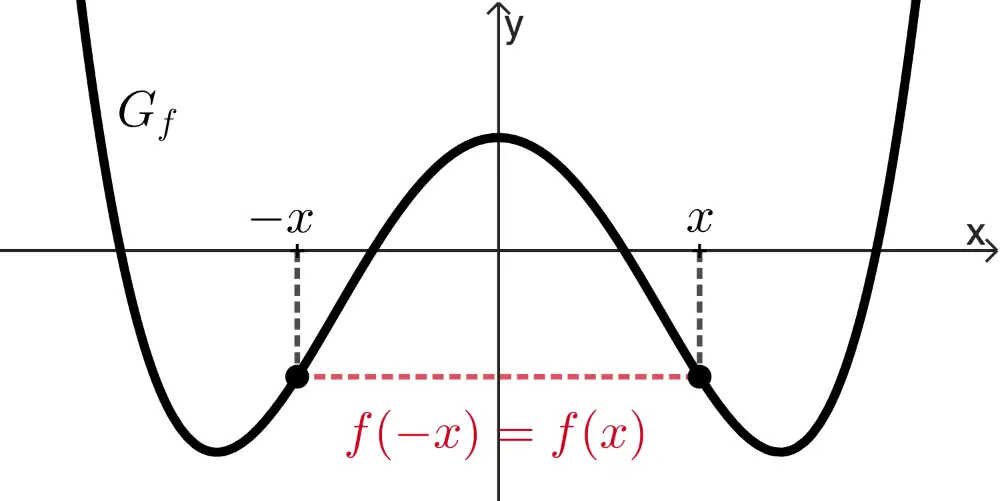
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
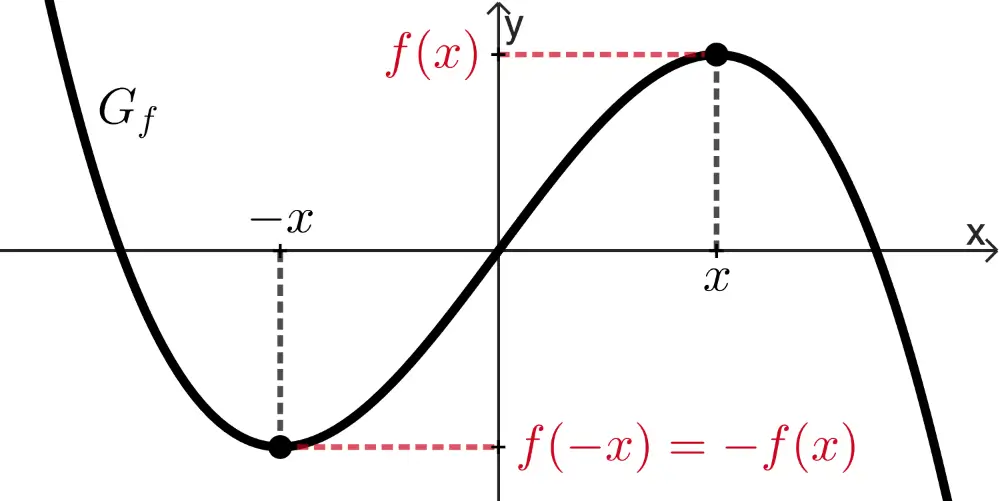
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(-x) = 3 \cdot (-x) + 2 + \frac{1}{(-x)^{2}} = -3x + 2 + \frac{1}{x^{2}}\]
\[\Longrightarrow \quad f(-x) \neq f(x); \; f(-x) \neq -f(x)\]
Der Graph \(G_{f}\) der Funktion \(f\) ist weder achsensymmetrisch zur \(y\)-Achse noch punktsymmetrisch zum Koordinatenursprung.
Art und Gleichungen aller Asymptoten der Funktion \(f\)
An einer Polstelle besitzt der Graph einer gebrochenrationalen Funktion eine senkrechte Asymptote. Eine mögliche waagrechte oder schräge Asymptote kennzeichnet das Verhalten des Graphen einer gebrochenrationalen Funktion im Unendlichen.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
Es ist also Folgendes zu untersuchen:
- Besitzt die Funktion \(f\) eine Polstelle?
- Grenzwertbetrachtung für \(x \to -\infty\) bzw. \(x \to +\infty\)
Anmerkung:
Die Aufgabenstellung verlangt lediglich danach, die Gleichungen der Asymptoten anzugeben. Eine schriftliche Begründung der Gleichungen kann entfallen.
Polstelle(n) der Funktion \(f\):
\[f(x) = 3x + 2 + \frac{1}{x^{2}}\]
Dem gebrochenrationalen Term \(\frac{1}{x^{2}}\) des Funktionsterms \(f(x)\) entnimmt man die Nennernullstelle \(x = 0\). Da die Division durch Null in der Mathematik nicht erlaubt ist, hat die gebrochenrationale Funktion \(f\) somit an der Stelle \(x = 0\) eine Definitionslücke. Der Definitionsbereich von \(f\) ergibt sich zu \(D_{f} = \mathbb R \backslash \{0\}\).
Da die Definitionslücke \(x = 0\) nicht zugleich Nullstelle des Zählers des gebrochenrationalen Terms \(\frac{1}{x^{2}}\) sein kann, ist die Definitionslücke \(x = 0\) nicht hebbar und somit eine Polstelle. Die doppelte Nullstelle \(x = 0\) des Terms \(\frac{1}{x^{2}}\) verweist auf eine Polstelle ohne Vorzeichenwechsel.
\(x = 0\) ist Polstelle.
\(\Longrightarrow \quad\)Senkrechte Asymptote mit der Gleichung \(x = 0\) (\(y\)-Achse)
Anmerkung:
Eine hebbare Definitionslücke einer gebrochenrationalen Funktion liegt immer dann vor, wenn eine Nennernullstelle zugleich Zählernullstelle ist und der Funktionsterm so gekürzt werden kann, dass keine Nennernullstelle mehr existiert. Der Graph der gebrochenrationalen Funktion zeigt dann an der entsprechenden Stelle ein Definitionsloch, während er an einer Polstelle gegen \(- \infty\) bzw. \(+ \infty\) strebt.
Grenzwertbetrachtung für \(x \to -\infty\) bzw. \(x \to +\infty\) (Verhalten im Unendlichen):
\[f(x) = 3x + 2 + \frac{1}{x^{2}}\]
\[\lim \limits_{x\,\to\,-\infty} f(x) = \lim \limits_{x\,\to\,-\infty} \underbrace{3x + 2}_{\to\,-\infty} + \underbrace{\frac{1}{x^{2}}}_{\to\,0} = -\infty\]
\[\lim \limits_{x\,\to\,+\infty} f(x) = \lim \limits_{x\,\to\,+\infty} \underbrace{3x + 2}_{\to\,+\infty} + \underbrace{\frac{1}{x^{2}}}_{\to\,0} = +\infty\]
Für \(x \to -\infty\) bzw. \(x \to +\infty\) wird der Wert des gerochenrationalen Terms \(\frac{1}{x^{2}}\) beliebig klein. Das Verhalten der gebrochenrationalen Funktion \(f\) wird im Unendlichen durch den linearen Term \(3x + 2\) bestimmt. Der Graph \(G_{f}\) nähert sich für \(x \to -\infty\) bzw. \(x \to +\infty\) asymptotisch der Geraden mit der Gleichung \(y = 3x + 2\) an.
\(\Longrightarrow \quad\)Schräge Asymptote mit der Gleichung \(y = 3x + 2\)
Anmerkung:
Ist eine gebrochenrationale Funktion \(f\) in der Form \(f(x) = g(x) + r(x)\) gegeben, wobei \(g(x)\) im Rahmen der abiturrelevanten Mathematik ein konstanter oder ein linearer Term ist, und \(r(x)\) ein gebrochenrationaler Term ist, so liefert \(y = g(x)\) die Gleichung der waagrechten bzw. schrägen Asymptote für das Verhalten des Graphen von \(f\) im Unendlichen.
Eine Stammfunktion der Funktion \(f\)
Anmerkung:
Es ist lediglich eine Stammfunktion der Funktion \(f\) anzugeben (vgl. Angabe). Jede Erklärung oder Rechnung kann entfallen.
\[f(x) = 3x + 2 + \frac{1}{x^{2}}\]
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
Jede differenzierbare Funktion \(F\) mit \(D_{F} = D_{f}\) für die \(F'(x) = f(x)\) gilt, ist eine Stammfunktion von \(f\).
Die Funktion \(f\) besitzt den maximalen Definitionsbereich \(D_{f} = \mathbb R \backslash \{0\}\).
Man erhält den Funktionsterm \(F(x)\) einer Stammfunktion von \(f\) durch „Aufleiten" des Funktionsterms \(f(x)\). Unter Berücksichtigung der Ableitung einer Potenzfunktion und der Summenregel ergibt sich eine Stammfunktion von \(f\) zu:
\[F(x) = \frac{3}{2}x^{2} + 2x - \frac{1}{x}; D_{F} = \mathbb R \backslash \{0\}\]
Erläuterung - „Aufleiten" von \(f(x)\):
Zunächst wird der Funktionsterm \(f(x)\) mithilfe der Rechenregel für Potenzen \(a^{-n} = \dfrac{1}{a^{n}}; \; a \in \mathbb R \backslash \{0\}, \; n \in \mathbb N\) vollständig in der Potenzschreibweise beschrieben.
\[\begin{align*}f(x) &= 3x + 2 + \frac{1}{x^{2}} & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= 3x + 2 + x^{-2} \end{align*}\]
Der Funktionsterm \(f(x)\) ist eine Summe. Gemäß der Summenregel sind die Summanden \(3x\), \(2\) und \(\frac{1}{x^{2}}\) das Ergebnis separater Ableitungen einer Stammfunktion \(F(x)\).
Entsprechend der Ableitung einer Potenzfunktion entsteht der Summand \(3x\) durch das Ableiten der Potenz \(x^{1 + 1} = x^{2}\). Da jedoch \(\left(x^{2}\right)' = 2x\) ist, muss der Faktor \(\frac{3}{2}\) korrigierend zur Potenz \(x^{2}\) hinzu gefügt werden.
Der konstante Summand \(2\) lässt sich auch als Potenzterm \(2 \cdot x^{0}\; (x^{0} = 1)\) schreiben. Entsprechend der Ableitung einer Potenzfunktion entsteht \(x^{0}\) durch das Ableiten der Potenz \(x^{0 + 1} = x\). Der Faktor \(2\) bleibt nach der Faktorregel als solcher erhalten.
Der Potenzterm \(x^{-2}\) entsteht durch das Ableiten der Potenz \(x^{-2 + 1} = x^{-1}\). Da jedoch \(\left( x^{-1} \right)' = (-1) \cdot x^{-2} = -x^{-2}\) ist, muss der Faktor \((-1)\) korrigierend zur Potenz \(x^{-1}\) hinzu gefügt werden.
\[\Longrightarrow \quad F(x) = \frac{3}{2} \cdot x^{2} + 2 \cdot x + (-1) \cdot x^{-1} = \frac{3}{2}x^{2} + 2x - \frac{1}{x}\]
Nachweis (Probe):
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*}F'(x) &= \left( \frac{3}{2}x^{2} + 2x - x^{-1} \right)' \\[0.8em] &= \frac{3}{2} \cdot 2 \cdot x + 2 - (-1) \cdot x^{-2} & &| \; a^{-n} = \frac{1}{a^{n}}\\[0.8em] &= 3x + 2 + \frac{1}{x^{2}} \\[0.8em] &= f(x)\end{align*}\]
Die Funktion \(F \colon x \mapsto \frac{3}{2}x^{2} + 2x - \frac{1}{x}\) ist eine Stammfunktion der Funktion \(f \colon x \mapsto 3x + 2 + \frac{1}{x^{2}}\) mit \(D_{F} = D_{f} = \mathbb R \backslash \{0\}\).

