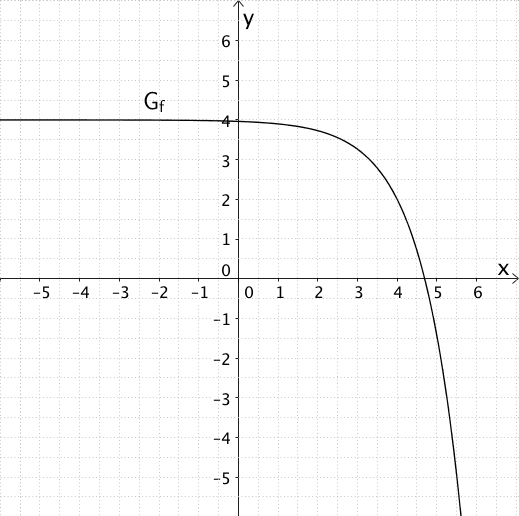
Die Abbildung zeigt den Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto 4 - 2e^{x - 4}\).
a) Geben Sie die Definitionsmenge der Funktion \(f\) an. Bestimmen Sie das Verhalten an den Rändern des Definitionsbereichs. Geben Sie die Wertemenge der Funktion \(f\) an.
b) Begründen Sie, dass die Funktion \(f\) umkehrbar ist.
c) Berechnen Sie die Umkehrfunktion \(f^{-1}\) der Funktion \(f\) und geben Sie die Definitions- und Wertemenge der Umkehrfunktion an. Skizzieren Sie den Graphen der Umkehrfunktion \(f^{-1}\) in das obige Koordinatensystem.
a) Definitionsmenge von \(f\), Verhalten an den Rändern des Definitionsbereichs und Wertemenge von \(f\)
Definitionsmenge der Funktion \(f\)
Anmerkung:
Die Definitionsmenge der Funktion \(f\) ist lediglich anzugeben. Jede Erklärung oder Rechnung kann entfallen.
\[f(x) = 4 - 2e^{x - 4}\]
Die Natürliche Exponentialfunktion \(x \mapsto e^{x}\) ist in \(\mathbb R\) definiert.
Der Graph der Funktion \(f\) geht aus dem Graphen der natürlichen Exponentialfunktion durch Spiegelung an der \(x\)-Achse, Streckung um den Faktor \(2\) in \(y\)-Richtung und Verschiebung um jeweils vier Einheiten in Richtung der positiven \(x\)- bzw. \(y\)-Achse hervor.
Durch die Entwicklung der Funktion \(f\) aus der Natürlichen Exponetialfunktion \(x \mapsto e^{x}\) ändert sich die Definitionsmenge nicht.
\[\Longrightarrow \quad D_{f} = \mathbb R\]
Verhalten an den Rändern des Definitionsbereichs der Funktion \(f\)
\[D_{f} = \mathbb R = ]-\infty;+\infty[\]
Es ist das Verhalten der Funktion \(f\) für \(x \to -\infty\) und \(x \to +\infty\) zu untersuchen.
\[f(x) = 4 - 2e^{x - 4}; \; D_{f} = \mathbb R\]
\[\lim \limits_{x\,\to\,-\infty} f(x) = \lim \limits_{x\,\to\,-\infty} \Big( 4 - \underbrace{2e^{x - 4}}_{\to\,0} \Big) = 4\]
\[\lim \limits_{x\,\to\,+\infty} f(x) = \lim \limits_{x\,\to\,+\infty} \Big( 4 - \underbrace{2e^{x - 4}}_{\to\,+\infty} \Big) = -\infty\]
Wertemenge der Funktion \(f\)
Anmerkung:
Die Wertemenge der Funktion \(f\) ist lediglich anzugeben. Jede Erklärung oder Rechnung kann entfallen.
Mit \(D_{f} = \mathbb R\) sowie \(\lim \limits_{x\,\to\,-\infty} f(x) = 4\) und \(\lim \limits_{x\,\to\,+\infty} f(x) = -\infty\) folgt:
\[W_{f} = \; ]-\infty;4[\]
b) Begründung, dass die Funktion \(f\) umkehrbar ist
\[f(x) = 4 - 2e^{x - 4}; \; D_{f} = \mathbb R\]
Begründung durch Rechnung
Kriterien für die Umkehrbarkeit einer Funktion
Eine Funktion \(f\,\colon\,\mapsto f(x)\) mit der Definitionsmenge \(D_{f}\) und der Wertemenge \(W_{f}\) heißt umkehrbar, falls es zu jedem \(y \in W_{f}\) genau ein \(x \in D_{f}\) mit \(f(x) = y\) gibt.
Ist eine Funktion auf Ihrer Definitionsmenge oder einer Teilmenge streng monoton (steigend oder fallend), so ist sie dort umkehrbar.
Die Funktion \(f\) ist in \(\mathbb R\) umkehrbar, wenn sie in \(\mathbb R\) streng monoton fallend oder steigend ist. Die Untersuchung des Monotonieverhaltens von \(f\) erfolgt mithilfe des Monotoniekriteriums.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Es ist zu untersuchen, ob für alle \(x \in \mathbb R\) entweder \(f'(x) < 0\) oder \(f'(x) > 0\) gilt.
Erste Ableitung \(f'\) bilden:
Die Funktion \(f\) wird mithilfe der Ableitung der natürlichen Exponentialfunktion, der Kettenregel, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel abgeleitet.
\[f(x) = 4 - 2e^{x - 4}; \; D_{f} = \mathbb R\]
Ableitung der natürlichen Exponentialfunktion
\[f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
(vgl. Merkhilfe)
\[f'(x) = 0 - 2 \cdot e^{x - 4} \cdot (1 - 0) = \underbrace{-2 \cdot \underbrace{e^{x - 4}}_{>\,0}}_{<\,0}\]
\(\Longrightarrow \quad\)Die Funktion \(f\) ist für alle \(x \in \mathbb R\) streng monoton fallend.
\(\Longrightarrow \quad\)Die Funktion \(f\) ist in \(\mathbb R\) umkehrbar.
Graphische Begründung
Kriterien für die Umkehrbarkeit einer Funktion
Eine Funktion \(f\,\colon\,\mapsto f(x)\) mit der Definitionsmenge \(D_{f}\) und der Wertemenge \(W_{f}\) heißt umkehrbar, falls es zu jedem \(y \in W_{f}\) genau ein \(x \in D_{f}\) mit \(f(x) = y\) gibt.
Ist eine Funktion auf Ihrer Definitionsmenge oder einer Teilmenge streng monoton (steigend oder fallend), so ist sie dort umkehrbar.
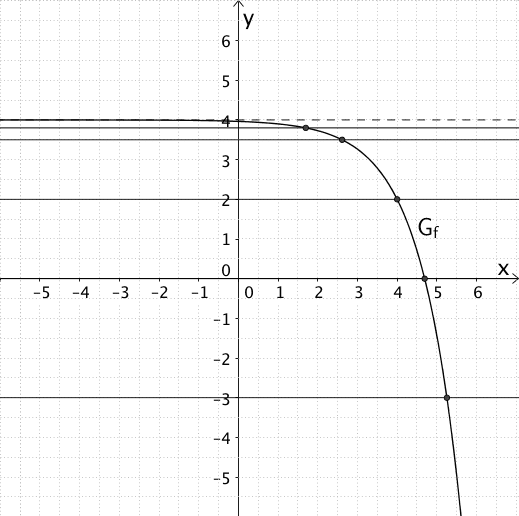
Zu jedem \(y \in W_{f}\) mit \(y = f(x)\) gibt es genau ein \(x \in D_{f}\), wenn jede Parallele zur \(x\)-Achse den Graphen \(G_{f}\) der Funktion \(f\) genau einmal schneidet.
Die Abbildung zeigt, dass \(G_{f}\) diese Voraussetzung erfüllt, wenngleich eine Dokumentation der Parallelen für \(x < 0\) aufgrund der Annäherung von \(G_{f}\) an die waagrechte Asymptote \(y = 4\) (vgl. Teilaufgabe a) schwierig ist.
\(\Longrightarrow \quad\)Die Funktion \(f\) ist in \(\mathbb R\) umkehrbar.
c) Umkehrfunktion \(f^{-1}\) der Funktion \(f\), Definitions- und Wertemenge der Umkehrfunktion sowie Skizzieren des Graphen der Umkehrfunktion
Umkehrfunktion \(f^{-1}\) der Funktion \(f\)
\[f(x) = 4 - 2e^{x - 4}; \; D_{f} = \mathbb R\]
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
Für die Bestimmung der Umkehrfunktion \(f^{-1}\) der Funktion \(f\) wird zunächst die Funktionsgleichung \(y = f(x)\) nach \(x\) aufgelöst. Anschließend werden die Variablen \(x\) und \(y\) getauscht und \(y = f^{-1}(x)\) liefert die Umkehrfunktion.
Es ergibt sich eine Exponentialgleichung. Diese lässt sich nach geeigneter elementarer Umformung durch Logarithmieren lösen.
\[\begin{align*} y &= f(x) \\[0.8em] y &= 4 - 2e^{x - 4} & &| + 2e^{x - 4} - y \\[0.8em] 2e^{x - 4} &= 4 - y & &| : 2 \\[0.8em] e^{x - 4} &= \frac{4 - y}{2} \\[0.8em] e^{x - 4} &= 2 - \frac{y}{2} & &| \; \ln \; \text{(Logarithmieren)} \\[0.8em] \ln\left( e^{x - 4} \right) &= \ln\left( 2 - \frac{y}{2} \right) & &| \; \ln{e^{x}} = x \; \left( \text{allg.:}\; \log_{a}{a^{x}} = x \right) \\[0.8em] x - 4 &= \ln\left( 2 - \frac{y}{2} \right) & &| + 4 \\[0.8em] x &= \ln\left( 2 - \frac{y}{2} \right) + 4 & &| \; x \longleftrightarrow y \; \text{(Variablentausch)} \\[0.8em] y &= \ln\left( 2 - \frac{x}{2} \right) + 4 & &| \; y = f^{-1}(x) \\[0.8em] f^{-1}(x) &= \ln\left( 2 - \frac{x}{2} \right) + 4 \end{align*}\]
Definitions- und Wertemenge der Umkehrfunktion \(f^{-1}\)
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
\(D_{f^{-1}} = W_{f} = \; ]-\infty;4[\) (vgl. Teilaufgabe a)
\(W_{f^{-1}} = D_{f} = \mathbb R\) (vgl. Teilaufgabe a)
Skizzieren des Graphen der Umkehrfunktion \(f^{-1}\)
Der Graph \(G_{f^{-1}}\) der Umkehrfunktion \(f^{-1}\) geht durch Spiegelung des Graphen \(G_{f}\) der Funktion \(f\) an der Winkelhalbierenden des ersten und dritten Quadranten mit der Gleichung \(y = x\) hervor.
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
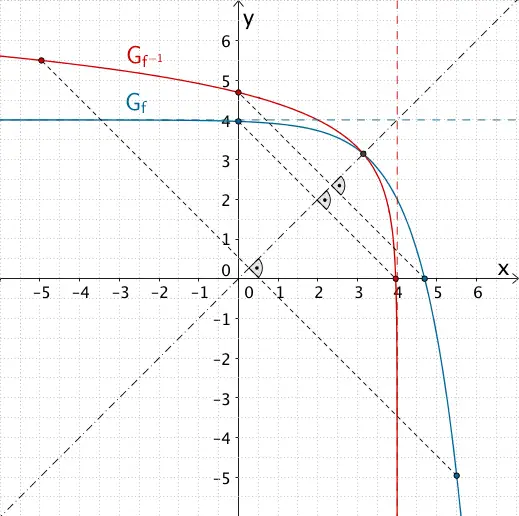
Spiegelt man beispielsweise die Schnittpunkte von \(G_{f}\) mit den Koordinatenachsen sowie einen weiteren geeigneten Punkt von \(G_{f}\) an der Winkelhalbierenden des ersten und dritten Quadranten, lässt sich damit der Graph \(G_{f^{-1}}\) der Umkehrfunktion \(f^{-1}\) mit hinreichender Genauigkeit skizzieren. Der Schnittpunkt von \(G_{f}\) mit der Winkelhalbierenden ist Fixpunkt der Spiegelung und damit gemeinsamer Punkt der Graphen \(G_{f}\) und \(G_{f^{-1}}\).

