Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto f(x)\) mit
\[f(x) = \vert 2x - 4 \vert = \begin{cases} \begin{align*} 2x - 4 \; \text{falls} \; &x \geq 2 \\[0.8em] -(2x - 4) \; \text{falls} \; &x < 2 \end{align*} \end{cases}\]
Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Skizzieren Sie \(G_{f}\) in ein geeignetes Koordinatensystem und begründen Sie geometrisch, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist.
b) Bestätigen Sie durch Rechnung, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist.
\[f(x) = \vert 2x - 4 \vert = \begin{cases} \begin{align*} 2x - 4 \; \text{falls} \; &x \geq 2 \\[0.8em] -(2x - 4) \; \text{falls} \; &x < 2 \end{align*} \end{cases}\]
a) Skizze von \(G_{f}\) und geometrische Begründung, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist
Skizze von \(G_{f}\)
Der Graph der Funktion \(f \colon x \mapsto \vert 2x - 4 \vert\) entsteht aus dem Graphen der Funktion \(x \mapsto 2x - 4\) (Gerade), indem alle unterhalb der \(x\)-Achse verlaufenden Teile des Graphen an der \(x\)-Achse gespiegelt werden und die oberhalb der \(x\)-Achse verlaufenden Teile des Graphen beibehalten werden.
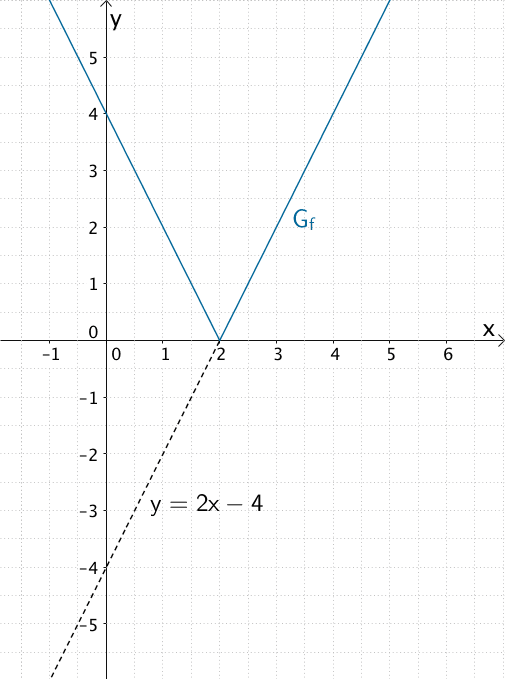
Verlauf des Graphen \(G_{f}\) der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \vert 2x - 4 \vert\)
Geometrische Begründung, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist
Der Graph \(G_{f}\) der Funktion \(f \colon x \mapsto \vert 2x - 4 \vert\) zeigt an der Stelle \(x = 2\) einen Knick. An der Knickstelle existiert keine eindeutige Steigung einer Tangente an \(G_{f}\). Da die Steigung einer Tangente an den Graphen einer Funktion die geometrische Bedeutung der Ableitung einer Funktion ist, ist die Funktion \(f\) somit an der Stelle \(x = 2\) nicht „ableitbar", also nicht differenzierbar.
b) Bestätigung durch Rechnung, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist
Die Funktion \(f \colon x \mapsto \vert 2x - 4 \vert\) ist an der Stelle \(x = 2\) nicht differenzierbar, weil der Differentialquotient \(\lim \limits_{x\, \to\, 2} \dfrac{f(x) - f(2)}{x - 2}\) nicht existiert. Denn die linksseitige Grenzwertbetrachtung \(\lim \limits_{x\, \to\, 2^{-}} \dfrac{f(x) - f(2)}{x - 2}\) und die rechtsseitige Grenzwertbetrachtung \(\lim \limits_{x\, \to\, 2^{+}} \dfrac{f(x) - f(2)}{x - 2}\) ergibt nicht denselben Grenzwert.
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
\[f(x) = \vert 2x - 4 \vert = \begin{cases} \begin{align*} 2x - 4 \; \text{falls} \; &x \geq 2 \\[0.8em] -(2x - 4) \; \text{falls} \; &x < 2 \end{align*} \end{cases}\]
Linksseitige Grenzwertbetrachtung:
\[\begin{align*}\lim \limits_{x\,\to\,2^{-}} \frac{f(x) - f(2)}{x - 2} &= \lim \limits_{x\,\to\,2^{-}} \frac{-(2x - 4) - [-(2 \cdot 2 - 4)]}{x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,2^{-}} \frac{-2x + 4}{x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,2^{-}} \frac{(-2) \cdot \cancel{(x - 2)}}{\cancel{(x - 2)}} \\[0.8em] &= -2 \end{align*}\]
Rechtsseitige Grenzwertbetrachtung:
\[\begin{align*}\lim \limits_{x\,\to\,2^{+}} \frac{f(x) - f(2)}{x - 2} &= \lim \limits_{x\,\to\,2^{+}} \frac{2x - 4 - (2 \cdot 2 - 4)}{x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,2^{+}} \frac{2x - 4}{x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,2^{+}} \frac{2 \cdot \cancel{(x - 2)}}{\cancel{(x - 2)}} \\[0.8em] &= 2 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad \lim \limits_{x\,\to\,2^{-}} \frac{f(x) - f(2)}{x - 2} &\neq \lim \limits_{x\,\to\,2^{+}} \frac{f(x) - f(2)}{x - 2} \\[0.8em] -2 &\neq 2 \end{align*}\]
\(\Longrightarrow \quad\)Die Funktion \(f \colon x \mapsto \vert 2x - 4 \vert\) ist an der Stelle \(x = 2\) nicht differenzierbar.

