Mathematik Klausur Q12/1-001 Bayern
Aufgabe 1
Berechnen Sie folgende Integrale bzw. die Integrationsgrenze \(a\) mit \(a \in \mathbb N\). Geben Sie exakte Werte an.
a) \(\displaystyle \int_{0}^{1} \frac{-6x^{2} + 6}{x^{3} - 3x + 3} dx\)
b) \(\displaystyle \int_{-a}^{3a} (3t - 2) dt = 4\)
c) \(\displaystyle \int_{1}^{\infty} \frac{3}{x^{2}} dx\)
d) \(\displaystyle \int_{4}^{8} \left( e^{-2x} -\sin\left(\frac{\pi}{4}x\right) +\frac{2}{x-2} \right) dx\)
Aufgabe 2
Geben sie jeweils eine Integrandenfunktion \(f(x)\) und \(g(x)\) an, sodass die folgenden Gleichungen erfüllt sind.
a) \(\displaystyle \int_{-a}^{+a} f(x) dx = 0; \; a \neq 0\)
b) \(\displaystyle \int_{-1}^{3} g(x) dx = 8\)
Aufgabe 3
Gegeben sind die jeweils in \(\mathbb R\) definierten Funktionenscharen \(f_{a} \colon x \mapsto x(a^{2} - x^{2})\) und \(g_{a} \colon x \mapsto x(x - a)^{2}\) mit \(a \in \mathbb R^{+}\).
a) Bestimmen Sie in Abhängigkeit des Parameters \(a\) den Flächeninhalt \(A(a)\) der Fläche, welche die Graphen der Funktionenscharen \(f\) und \(g\) begrenzen.
b) Für welchen Wert des Parameters \(a\) ergibt sich der Flächeninhalt 13,5 FE (Flächeneinheiten)?
Aufgabe 4
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto \dfrac{1}{20}x^{5} + \dfrac{1}{12}x^{4} - \dfrac{1}{3}x^{3}\).
Bestimmen Sie die Wendepunkte des Graphen \(G_{f}\) der Funktion \(f\) und geben Sie das Kümmungsverhalten von \(G_{f}\) an.
Aufgabe 5
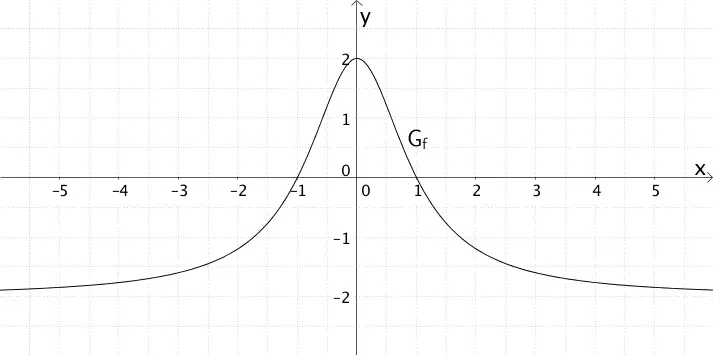
Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(R\) definierten Funktion \(f\).
a) Skizzieren Sie den Graphen \(G_{F}\) der Integralfunktion \(F \colon x \mapsto \displaystyle \int_{0}^{x} f(t) dt\) in die Abbildung. Gehen Sie dabei insbesondere auf die Nullstellen und die Extremstelle von \(G_{f}\) sowie auf das Verhalten von \(G_{f}\) für \(x \to \pm \infty\) ein. Erläutern Sie Ihre Vorgehensweise.
b) „Jede Stammfunktion der abgebildeten Funktion \(f\) ist eine Integralfunktion." Nehmen Sie zu dieser Aussage begründend Stellung, indem Sie sich auf \(G_{F}\) beziehen.
- Details
- Hauptkategorie: Klausuren Q12/1
Berechnen Sie folgende Integrale bzw. die Integrationsgrenze \(a\) mit \(a \in \mathbb N\). Geben Sie exakte Werte an.
a) \(\displaystyle \int_{0}^{1} \frac{-6x^{2} + 6}{x^{3} - 3x + 3} dx\)
b) \(\displaystyle \int_{-a}^{3a} (3t - 2) dt = 4\)
c) \(\displaystyle \int_{1}^{\infty} \frac{3}{x^{2}} dx\)
d) \(\displaystyle \int_{4}^{8} \left( e^{-2x} -\sin\left(\frac{\pi}{4}x\right) +\frac{2}{x-2} \right) dx\)
- Details
- Hauptkategorie: Klausuren Q12/1
Geben sie jeweils eine Integrandenfunktion \(f(x)\) und \(g(x)\) an, sodass die folgenden Gleichungen erfüllt sind.
a) \(\displaystyle \int_{-a}^{+a} f(x) dx = 0; \; a \neq 0\)
b) \(\displaystyle \int_{-1}^{3} g(x) dx = 8\)
- Details
- Hauptkategorie: Klausuren Q12/1
Gegeben sind die jeweils in \(\mathbb R\) definierten Funktionenscharen \(f_{a} \colon x \mapsto x(a^{2} - x^{2})\) und \(g_{a} \colon x \mapsto x(x - a)^{2}\) mit \(a \in \mathbb R^{+}\).
a) Bestimmen Sie in Abhängigkeit des Parameters \(a\) den Flächeninhalt \(A(a)\) der Fläche, welche die Graphen der Funktionenscharen \(f\) und \(g\) begrenzen.
b) Für welchen Wert des Parameters \(a\) ergibt sich der Flächeninhalt 13,5 FE (Flächeneinheiten)?
- Details
- Hauptkategorie: Klausuren Q12/1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto \dfrac{1}{20}x^{5} + \dfrac{1}{12}x^{4} - \dfrac{1}{3}x^{3}\).
Bestimmen Sie die Wendepunkte des Graphen \(G_{f}\) der Funktion \(f\) und geben Sie das Kümmungsverhalten von \(G_{f}\) an.
- Details
- Hauptkategorie: Klausuren Q12/1
Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(R\) definierten Funktion \(f\).
a) Skizzieren Sie den Graphen \(G_{F}\) der Integralfunktion \(F \colon x \mapsto \displaystyle \int_{0}^{x} f(t) dt\) in die Abbildung. Gehen Sie dabei insbesondere auf die Nullstellen und die Extremstelle von \(G_{f}\) sowie auf das Verhalten von \(G_{f}\) für \(x \to \pm \infty\) ein. Erläutern Sie Ihre Vorgehensweise.
b) „Jede Stammfunktion der abgebildeten Funktion \(f\) ist eine Integralfunktion." Nehmen Sie zu dieser Aussage begründend Stellung, indem Sie sich auf \(G_{F}\) beziehen.
- Details
- Hauptkategorie: Klausuren Q12/1
2023 Christian Rieger・mathelike
