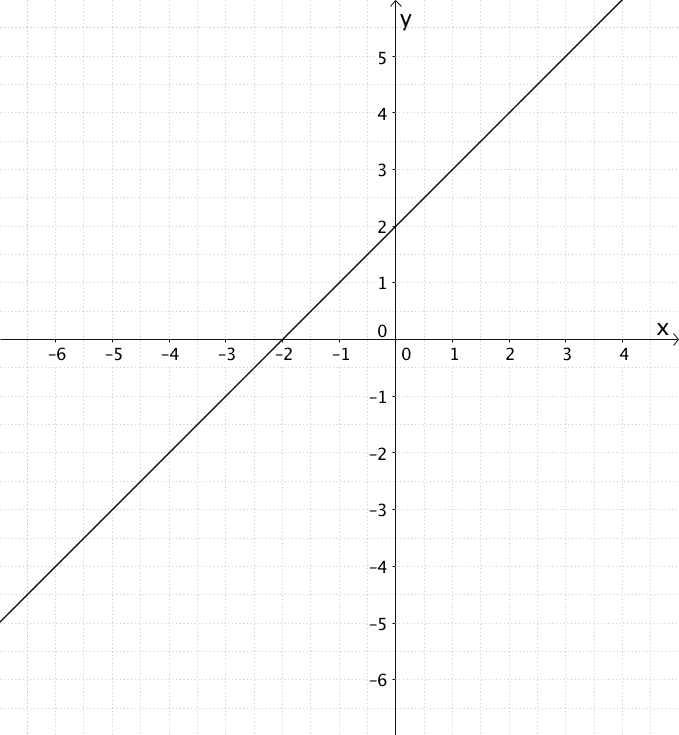
Die Abbildung zeigt den Graphen der Ableitungsfunktion \(f'\) einer auf \(\mathbb R\) differenzierbaren Funktion \(f\).
a) Geben Sie das Monotonieverhalten und die Extremstelle(n) von \(f\) an.
b) Ermitteln Sie den Funktionsterm der Funktion \(f\), deren Graph \(G_{f}\) durch den Punkt \(P(1|-1)\) verläuft und skizzieren Sie \(G_{f}\).
a) Monotonieverhalten und Extremstelle(n) von \(f\)
Monotonieverhalten von \(f\)
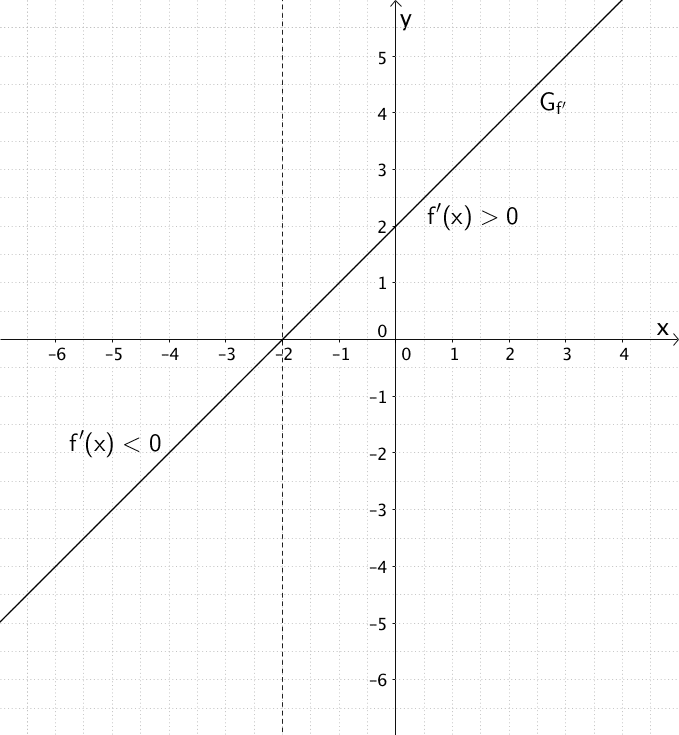
Vorzeichenwechsel von \(f'\) an der Stelle \(x = -2\)
Der Abbildung entnimmt man:
\(f'(x) < 0\) für \(x \in \; ]-\infty;-2[\)
\(f'(x) > 0\) für \(x \in \; ]-2;+\infty[\)
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Nach dem Monotoniekriterium folgt daraus:
\(G_{f}\) ist im Intervall \(]-\infty;-2[\) streng monoton fallend.
\(G_{f}\) ist im Intervall \(]-2;+\infty[\) streng monoton steigend.
Extremstelle(n) von \(f\)
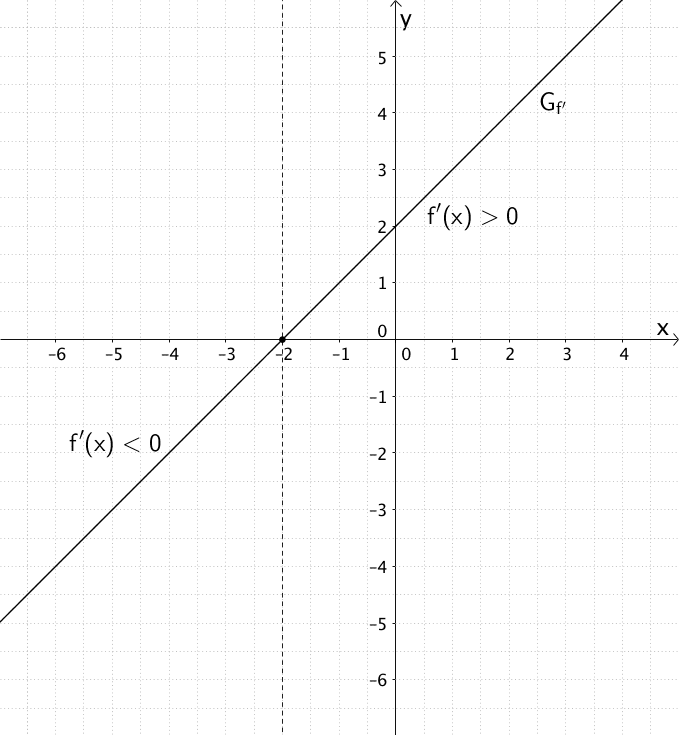
Nullstelle \(x = -2\) mit Vorzeichenwechsel von \(f'\)
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
Die notwendige Bedingung für eine Extremstelle von \(f\) lautet: \(f'(x) = 0\). Die Abbildung zeigt, dass \(x = -2\) einzige Nullstelle von \(f'\) ist. Da \(f'\) an der Stelle \(x = -2\) zudem das Vorzeichen wechselt, muss es sich um eine Extremstelle handeln.
Der Nachweis der Art der Extremstelle ist in diesem Fall nicht zu erbringen.
Anmerkung:
Da \(G_{f}\) an der Stelle \(x = -2\) das Monotonieverhalten von streng monoton fallend nach streng monoton steigend wechselt, besitzt \(G_{f}\) an der Stelle \(x = -2\) den Tiefpunkt \(TiP(-2|f(-2))\).
Veranschaulichung mithilfe einer Monotonietabelle (Ergänzung):
| \(x < -2\) | \(x = -2\) | \(x > -2\) | |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\searrow\) | \(TiP(-2|f(-2))\) | \(\nearrow\) |
b) Funktionsterm der Funktion \(f\), deren Graph \(G_{f}\) durch den Punkt \(P(1|-1)\) verläuft und Skizze von \(G_{f}\)
Funktionsterm der Funktion \(f\), deren Graph \(G_{f}\) durch den Punkt \(P(1|-1)\) verläuft
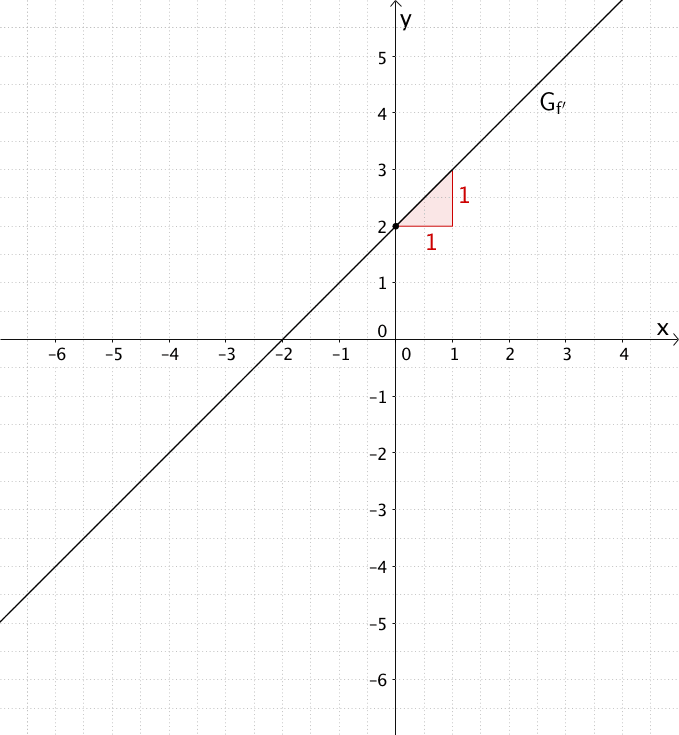
Der Funktionsterm der Ableitungsfunktion \(f'\) lässt sich der Abbildung zu \(f'(x) = x + 2\) entnehmen.
Die gesuchte Funktion \(f\), deren Graph \(G_{f}\) durch den Punkt \(P(1|-1)\) verläuft, ist eine Stammfunktion der Ableitungsfunktion \(f'\). Man erhält den Funktionsterm der Menge aller Stammfunktionen von \(f'\) durch „Aufleiten" des Funktionsterms \(f'(x)\).
Stammfunktion
Eine differenzierbare Funktion \(F\) heißt eine Stammfunktion der Funktion \(f\), wenn für alle \(x \in D_f\) gilt:
\(F'(x) = f(x)\)
\[f'(x) = x + 2\]
Aufleiten von \(f'(x)\) ergibt:
\[f(x) = \frac{1}{2}x^{2} + 2x + C\]
Nachweis (Probe):
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\left( \frac{1}{2}x^{2} + 2x + C \right)' = \frac{1}{2} \cdot 2 \cdot x + 2 + 0 = x + 2 = f'(x)\]
Erläuterung - „Aufleiten" von \(f(x)\):
Der Funktionsterm \(f'(x)\) ist eine Summe. Gemäß der Summenregel sind die Summanden \(x\) und \(2\) das Ergebnis separater Ableitungen zweier Summanden von \(f(x)\).
Entsprechend der Ableitung einer Potenzfunktion muss der Summand \(x\) durch das Ableiten der Potenz \(x^{1 + 1} = x^{2}\) entstehen. Da jedoch \(\left[ x^{2} \right]' = 2x\) ist, muss der Faktor \(\frac{1}{2}\) zur Potenz \(x^{2}\) korrigierend hinzu gefügt werden.
Das Aufleiten des konstanten Summanden \(2\) lässt sich ebenfalls mithilfe der Ableitung einer Potenzfunktion erklären. Schreibt man \(2 = 2 \cdot x^{0} \; (x^{0} = 1)\), so muss die Potenz \(x^{0}\) durch das Ableiten der Potenz \(x^{0 + 1} = x\) entstehen. Der Faktor \(2\) bleibt gemäß der Faktorregel beim Ableiten als solcher erhalten.
Durch eine additive Konstante \(C\) mit \(C \in \mathbb R\), deren Ableitung gleich Null ist, entsteht der Funktionsterm \(f(x)\) der Menge aller Stammfunktionen von \(f'(x)\)
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Die Konstante \(C\) bewirkt eine Verschiebung der Graphen von \(f\) in \(y\)-Richtung.
Um nun genau diejenige Funktion \(f\) zu erhalten, deren Graph \(G_{f}\) durch den Punkt \(P(1|-1)\) verläuft, setzt man die Koordinaten von \(P\) in die Funktionsgleichung \(y = f(x) = \frac{1}{2}x^{2} + 2x + C\) ein und löst die Gleichung nach \(C\) auf.
\[P(1|-1) \in G_{f}\]
\[y = f(x) = \frac{1}{2}x^{2} + 2x + C\]
\[\begin{align*}-1 &= \frac{1}{2} \cdot 1^{2} + 2 \cdot 1 + C \\[0.8em] -1 &= 2{,}5 + C & &| - 2{,}5 \\[0.8em] -3{,}5 &= C \end{align*}\]
\[\Longrightarrow \quad f(x) = \frac{1}{2}x^{2} + 2x -3{,}5\]
Der Graph \(G_{f}\) der Funktion \(f \colon x \mapsto \dfrac{1}{2}x^{2} + 2x -3{,}5\) verläuft durch den Punkt \(P(1|-1)\).
Skizze von \(G_{f}\)
Der Graph der Funktion \(f \colon x \mapsto \dfrac{1}{2}x^{2} + 2x -3{,}5\) ist eine nach oben geöffnete Parabel, deren Scheitelpunkt an der Stelle \(x = -2\) einziger Extrempunkt (Tiefpunkt) von \(G_{f}\) ist.
Anmerkung:
Die Skizze sollte erkennen lassen, dass \(x = -2\) Extremstelle von \(G_{f}\) ist. Eine Kennzeichnung der exakten Lage des Extrempunkts (Tiefpunkts) ist bei dieser Aufgabe nicht erforderlich (vgl. Teilaufgabe a).
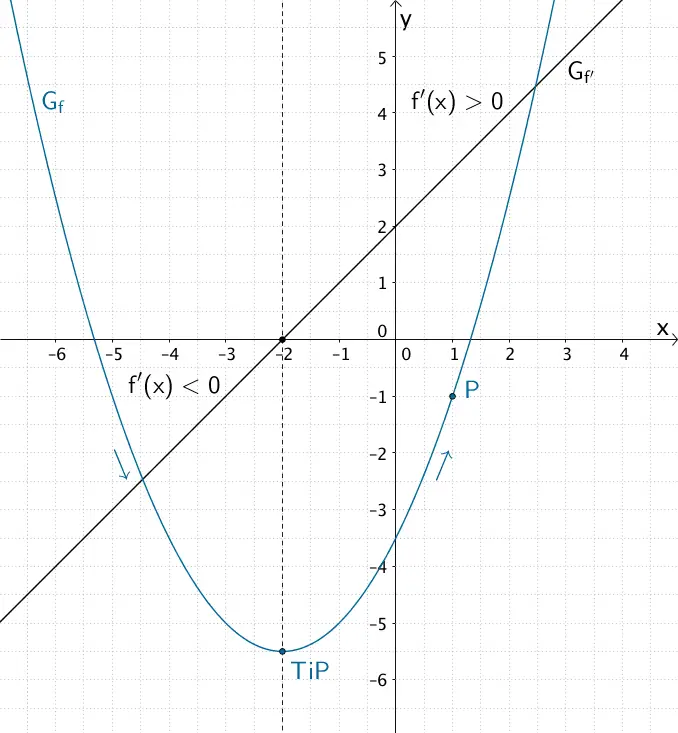
Graph \(G_{f}\) der Funktion \(f \colon x \mapsto \dfrac{1}{2}x^{2} + 2x -3{,}5\) durch den Punkt \(P(1|-1)\)

