Mathematik Abitur Bayern 2015

Die beiden Diagramme zeigen für die Bevölkerungsgruppe der über 14-jährigen in Deutschland Daten zur Altersstruktur und zum Besitz von Mobiltelefonen.

Aus den über 14-jährigen in Deutschland wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:

\(M\): „Die Person besitzt ein Mobiltelefon."

\(S\): „Die Person ist 65 Jahre oder älter."

\(E\): „Mindestens eines der Ereignisse \(M\) und \(S\) tritt ein."

Geben Sie an, welche zwei der folgenden Mengen I bis VI jeweils das Ereignis \(E\) beschreiben.

(2 BE)

An den betrachteten geraden Abschnitt der Achterbahn schließt sich - in Fahrtrichtung gesehen - eine Rechtskurve an, die im Modell durch einen Viertelkreis beschrieben wird, der in der Ebene \(E\) verläuft und den Mittelpunkt \(M \left( 0|3\sqrt{2}|2 \right)\) hat.

Das Lot von \(M\) auf \(g\) schneidet \(g\) im Punkt \(B\). Im Modell stellt \(B\) den Punkt der Achterbahn dar, in dem der gerade Abschnitt endet und die Kurve beginnt. Bestimmen Sie die Koordinaten von \(B\) und berechnen Sie den Kurvenradius im Modell.

(Teilergebnis: \(B\left( -1|2\sqrt{2}|3 \right)\)) 

(5 BE)

Die \(x_{1}x_{2}\)-Ebene beschreibt modellhaft eine horizontale Fläche, auf der eine Achterbahn errichtet wurde. Ein gerader Abschnitt der Bahn beginnt im Modell im Punkt \(A\) und verläuft entlang der Geraden \(g\). Der Vektor \(\displaystyle \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\) beschreibt die Fahrtrichtung auf diesem Abschnitt.

Berechnen Sie im Modell die Größe des Winkels, unter dem dieser Abschnitt der Achterbahn gegenüber der Horizontalen ansteigt.

(3 BE)

Berechnen Sie \(\displaystyle \int_{2}^{4} g(t)\,dt\) und deuten Sie den Wert des Integrals im Sachzusammenhang.

(Teilergebnis: Wert des Integrals: 0,5)

(4 BE)

Gegeben ist die Funktion \(f\) mit \(f(x) = x^3 - 6x^2 + 11x - 6\) und \(x \in \mathbb R\).

Weisen Sie nach, dass der Wendepunkt des Graphen von \(f\) auf der Geraden mit der Gleichung \(y = x - 2\) liegt.

(3 BE)

Erläutern Sie anhand eines Beispiels, dass die modellhafte Beschreibung der Schießeinlage durch eine Bernoullikette unter Umständen der Realität nicht gerecht wird.

(2 BE)

Bei der Wintersportart Biathlon wird bei jeder Schießanlage auf fünf Scheiben geschossen. Ein Biathlet tritt bei einem Einzelrennen zu einer Schießeinlage an, bei der er auf jede Scheibe einen Schuss abgibt. Diese Schießeinlage wird modellhaft durch eine Bernoullikette mit der Länge 5 und der Trefferwahrscheinlichkeit \(p\) beschrieben.

Geben Sie für die folgenden Ereignisse \(A\) und \(B\) jeweils einen Term an, der die Wahrscheinlichkeit des Ereignisses in Abhängigkeit von \(p\) beschreibt.

\(A\): „Der Biathlet trifft bei genau vier Schüssen."

\(B\): „Der Biathlet trifft nur bei den ersten beiden Schüssen."

(3 BE)

Die Punkte \(A\), \(B\) und \(E\,(1|2|5)\) sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunkts gibt es mehrere Möglichkeiten.

Geben Sie für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunkts an.

(2 BE)

Um 6 Uhr verläuft der Schatten des Polstabs im Modell durch den Mittelpunkt der Kante \([BC]\), um 12 Uhr durch den Mittelpunkt der Kante \([AB]\) und um 18 Uhr durch den Mittelpunkt der Kante \([AD]\). Begründen Sie, dass der betrachtete Zeitpunkt \(t_{0}\) vor 12 Uhr liegt.

(2 BE)

Abbildung 1 zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(p \colon x \mapsto 0{,}5 \cdot (x + 2)^2 - 0{,}5\), die die Nullstellen \(x = -3\) und \(x = -1\) hat.

Für \(x \in D_{f}\) gilt \(\displaystyle f(x) = \frac{1}{p(x)}\).

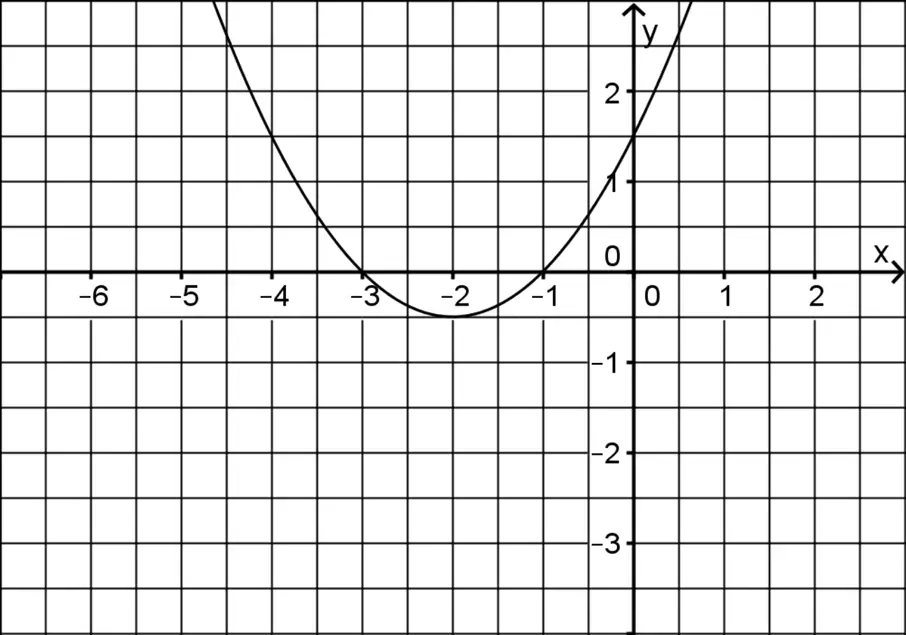Abb. 1

Gemäß der Quotientenregel gilt für die Ableitung \(f'\) und \(p'\) die Beziehung \(\displaystyle f'(x) = -\frac{p'(x)}{\big( p(x) \big)^2}\) für \(x \in D_{f}\).

Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von \(f'(x)\) und \(p'(x)\), dass \(x = -2\) einzige Nullstelle von \(f'\) ist und dass \(G_{f}\) in \(]-3;-2[\) streng monoton steigend sowie in \(]-2;1[\) streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von \(G_{f}\) an.

(5 BE)

Der Graph \(G_{f}\) einer in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto ax^4 + bx^3\) mit \(a,b \in \mathbb R\) besitzt im Punkt \(O\,(0|0)\) einen Wendepunkt mit waagrechter Tangente.

\(W\,(1|-1)\) ist ein weiterer Wendepunkt von \(G_{f}\). Bestimmen Sie mithilfe dieser Informationen die Werte von \(a\) und \(b\).

(Ergebnis: \(a = 1, b = -2\))

(4 BE)

Gegeben ist die Funktion \(f \colon x \mapsto \left(x^3 - 8 \right) \cdot (2 + \ln x)\) mit maximalem Definitionsbereich D.

Geben Sie D an.

(1 BE)

Die Punkte \(A\), \(B\) und \(E\,(1|2|5)\) sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunkts gibt es mehrere Möglichkeiten.

Geben Sie für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunkts an.

(2 BE)

Gegeben ist die Funktion \(f\) mit \(f(x) = x^3 - 6x^2 + 11x - 6\) und \(x \in \mathbb R\).

Weisen Sie nach, dass der Wendepunkt des Graphen von \(f\) auf der Geraden mit der Gleichung \(y = x - 2\) liegt.

(3 BE)

(2 BE)

Die Gerade \(g\) verläuft durch die Punkte \(A\,(0|1|2)\) und \(B\,(2|5|6)\).

Zeigen Sie, dass die Punkte \(A\) und \(B\) den Abstand 6 haben.

Die Punkte \(C\) und \(D\) liegen auf \(g\) und haben von \(A\) jeweils den Abstand 12. Bestimmen Sie die Koordinaten von \(C\) und \(D\).

(3 BE)

Beim Atmen ändert sich das Luftvolumen in der Lunge. Geben Sie auf der Grundlage des Modells einen Zeitpunkt an, zu dem das Luftvolumen in der Lunge der Testperson minimal ist, und machen Sie Ihre Antwort mithilfe von Abbildung 5 plausibel.

(2 BE)

Berechnen Sie \(f(-5)\) und \(f(-1{,}5)\) und skizzieren Sie \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1.

(4 BE)

Bestimmen Sie Lage und Art des Extrempunkts von \(G_{f}\).

(4 BE)

Entscheiden Sie, ob bei der Abwägung, die zur Wahl der Nullhypothese II führte, die Befürchtung eines Imageverlustes oder die Kostenfrage als schwerwiegender erachtet wurde. Erläutern Sie Ihre Entscheidung.

(3 BE)