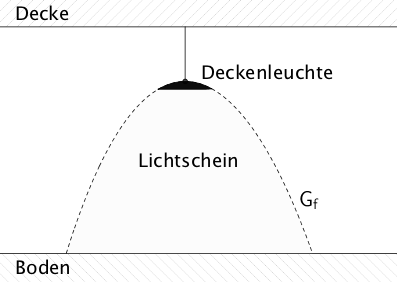
An der Decke eines Hausflurs ist eine Deckenleuchte angebracht. Die Randlinie des Lichtkegels der Deckenleuchte kann näherungsweise durch die Funktion \(\displaystyle f \colon x \mapsto -3 \cdot \left( e^{0{,}4x} + e^{-0{,}5x} \right) + 9\) beschrieben werden mit \(x\) und \(y\) in Metern (vgl. Abbildung). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Zeigen Sie, dass \(G_{f}\) nicht symmetrisch bezüglich des Koordinatensystems ist.
b) Ersetzen Sie einen Zahl \((\neq 0)\) des Funktionsterms \(f(x)\) so, dass \(G_{f}\) symmetrisch ist und geben Sie die Art der Symmetrie an.
Eine Feinjustierung der LEDs der Deckenleuchte verändert den Lichtkegel. Die Randlinie des veränderten Lichtkegels wird nun näherungsweise durch die Funktion \(g \colon x \mapsto -3 \cdot \left( e^{0{,}5x} + e^{-0{,}5x} \right) + 9\) beschrieben. Der Graph der Funktion \(g\) wird mit \(G_{g}\) bezeichnet.
c) Bestimmen Sie die Schnittpunkte von \(G_{g}\) mit den Koordinatenachsen. Hinweis: Verwenden Sie die Substitution \(u = e^{0{,}5x}\) zur Bestimmung der Schnittpunkte mit der \(x\)-Achse.
d) Berechnen Sie den Winkel, unter dem \(G_{g}\) die negative \(x\)-Achse schneidet.
e) Die Position der Aufhängung der Deckenleuchte entspricht der Lage des Hochpunkts von \(G_{g}\). Die Aufhängung ist 85 cm von der Decke entfernt. Berechnen Sie die Raumhöhe \(h\) des Hausflurs, an dessen Decke die Deckenleuchte angebracht ist.