Die Graphen der Schar lassen sich in die beiden folgenden Gruppen I und II einteilen:
I Der Graph hat genau zwei Extrempunkte.
II Der Graph hat keine Extrempunkte.
Die Abbildung 2 zeigt einen Graphen der Gruppe I, die Abbildung 3 einen Graphen der Gruppe II.
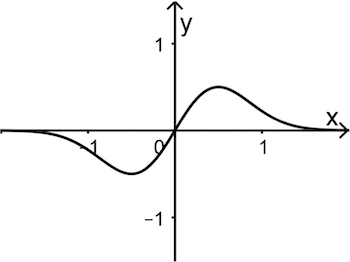Abb. 2
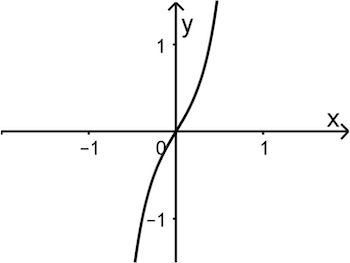Abb. 3
Die Extremstellen von \(f_a\) stimmen mit den Lösungen der Gleichung \(a \cdot x^2 = 1\) überein.
Geben Sie zu jeder der beiden Gruppen I und II alle zugehörigen Werte von \(a\) an und begründen Sie Ihre Angabe.
(3 BE)
