Exponentielle Wachstums- und Abklingfunktion
Zeitabhängige Wachstums- und Abklingprozesse verlaufen häufig exponentiell und lassen sich durch streng monoton wachsende bzw. streng monoton fallende Exponentialfunktionen beschreiben.
Exponentielle Wachstumsfunktion
\[N(t) = N_{0} \cdot e^{k \cdot t}\]
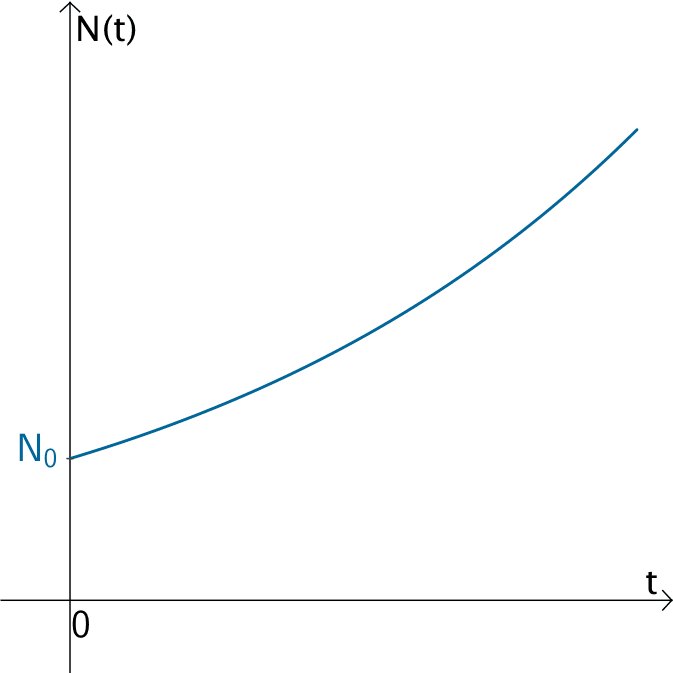
Graph einer exponentiellen Wachstumsfunktion \(N \colon t \mapsto N_{0} \cdot e^{k \cdot t}\)
Exponentielle Abklingfunktion
\[N(t) = N_{0} \cdot e^{-k \cdot t}\]
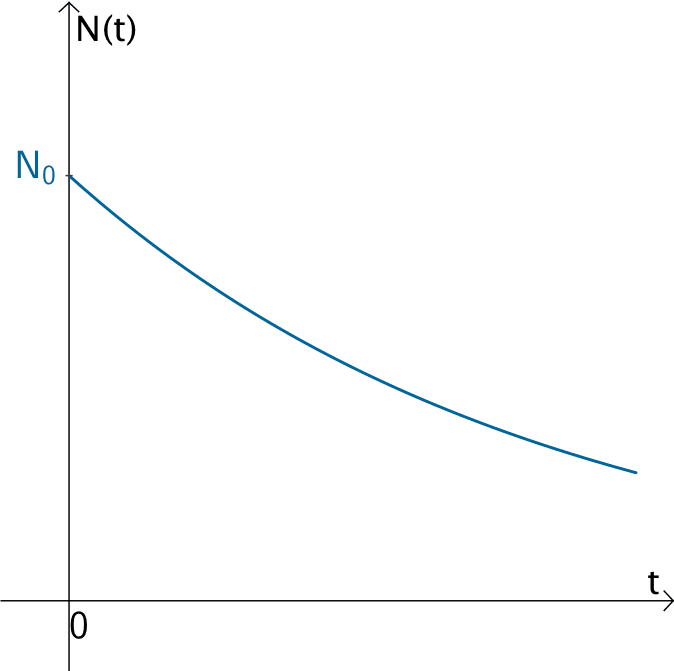
Graph einer exponentiellen Abklingfunktion \(N \colon t \mapsto N_{0} \cdot e^{-k \cdot t}\)
Dabei bezeichnet
- \(N_{0}\) mit \(N_{0} > 0\) den Startwert zum Zeitpunkt \(t = 0\) (Beobachtungsbeginn),
- \(t\) mit \(t \geq 0\) die Zeit seit Beginn der Beobachtung,
- \(k\) mit \(k > 0\) die Wachstums- bzw. Abklingkonstante und
- \(N(t)\) den Wert nach der Zeit \(t\).
Beispielaufgabe
Eine Statistik gibt den durchschnittlichen jährlichen Wertverlust eines PKWs der Marke X mit 15 % an. Die Funktion \(W \colon t \mapsto W_{0} \cdot e^{-0{,}163 \cdot t}\) beschreibt näherungsweise den Wert \(W\) eines PKWs der Marke X (in Euro) in Abhängigkeit von der Zeit \(t\) (in Jahren). Dabei bedeutet \(W_{0}\) den Neuwert eines PKWs der Marke X in Euro.
Nach wie vielen Jahren beträgt der Wert eines PKWs der Marke X noch 50 % seines Neuwerts?
\[W(t) = W_{0} \cdot e^{-0{,}163 \cdot t}\]
Nach \(t\) Jahren soll der Wert eines PKWs der Marke X noch \(0{,}5 \cdot W_{0}\) Euro betragen.
\[\Longrightarrow \quad W(t) = 0{,}5 \cdot W_{0}\]
\[\begin{align*} W(t) &= W_{0} \cdot e^{-0{,}163 \cdot t} \\[0.8em] 0{,}5 \cdot W_{0} &= W_{0} \cdot e^{-0{,}163 \cdot t} & &| : W_{0} \\[0.8em] 0{,}5 &= e^{-0{,}163 \cdot t} & &| \; \ln(\dots) \; \text{(Logarithmieren)} \\[0.8em] \ln{0{,}5} &= \ln\left( e^{-0{,}163 \cdot t} \right) & &| \;\ln(e^{x}) = x \\[0.8em] \ln{0{,}5} &= -0{,}163 \cdot t & &| : (-0{,}163) \\[0.8em] \frac{\ln{0{,}5}}{-0{,}163} &= t \\[0.8em] 4{,}25 &\approx t \end{align*}\]
Laut vorliegender Statistik beträgt der Wert eines PKWs der Marke X nach etwa 4,25 Jahren noch 50 % des Neuwerts.
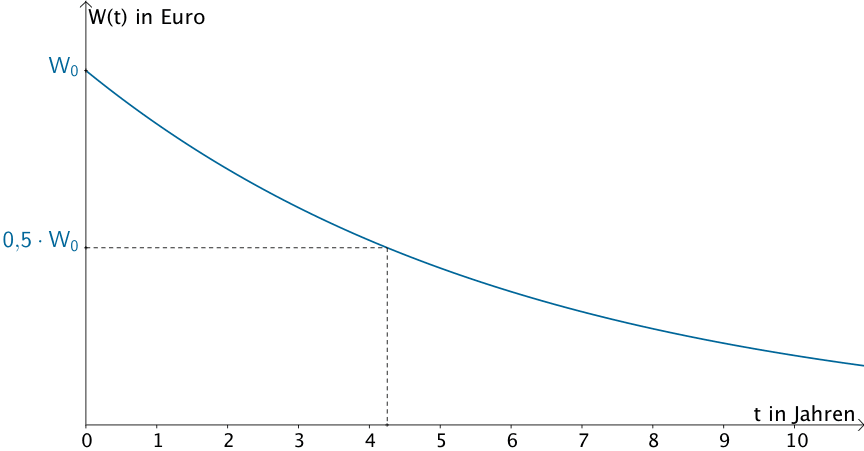
Graph der Wertverlustfunktion \(W \colon t \mapsto W_{0} \cdot e^{-0{,}163 \cdot t}\) eines PKWs der Marke X

