Lagebeziehungen zweier Geraden
Bei der gegenseitigen Lage zweier Geraden \(g\) und \(h\) lassen sich vier Fälle unterscheiden:
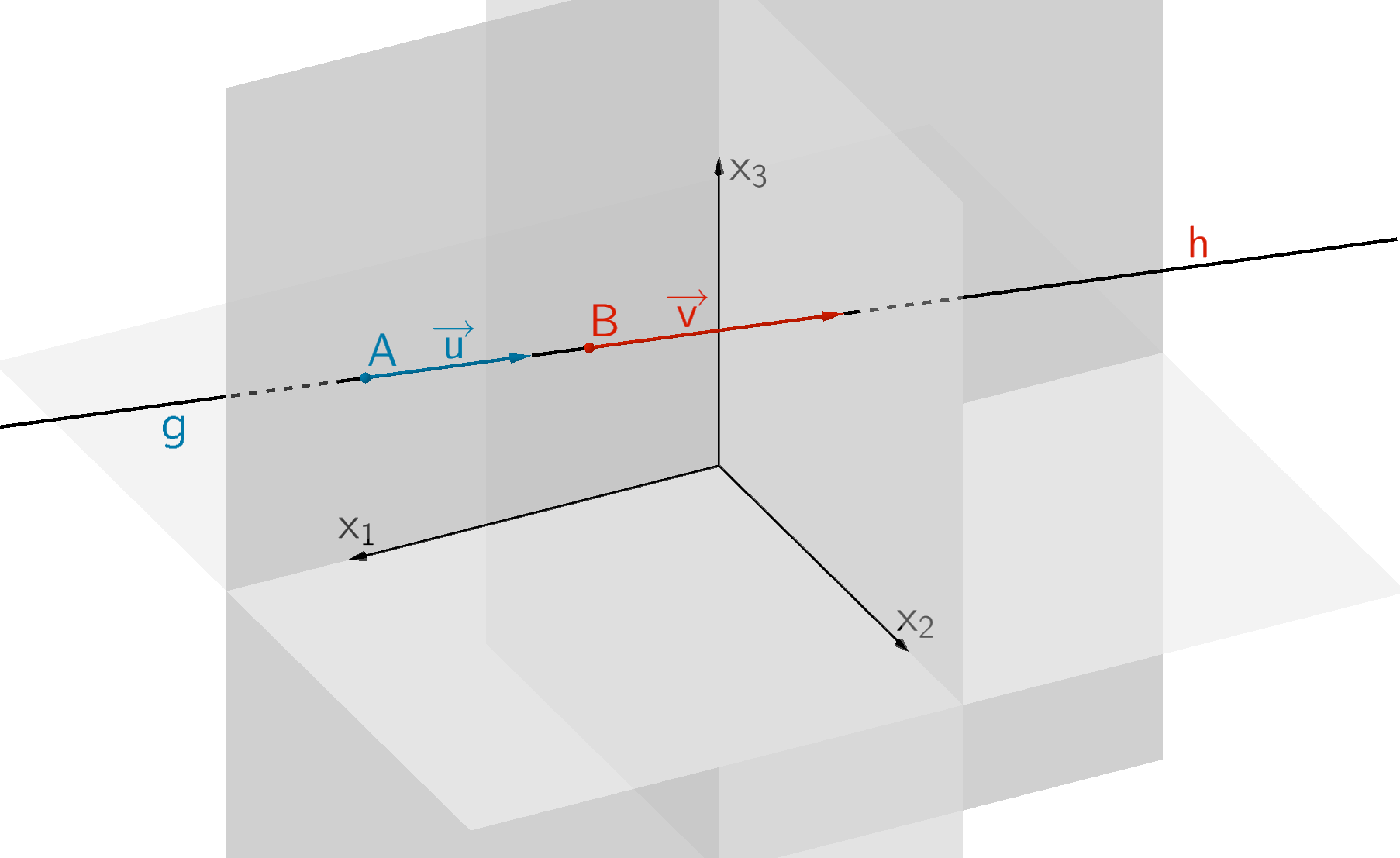
Die Geraden \(g\) und \(h\) sind identisch.
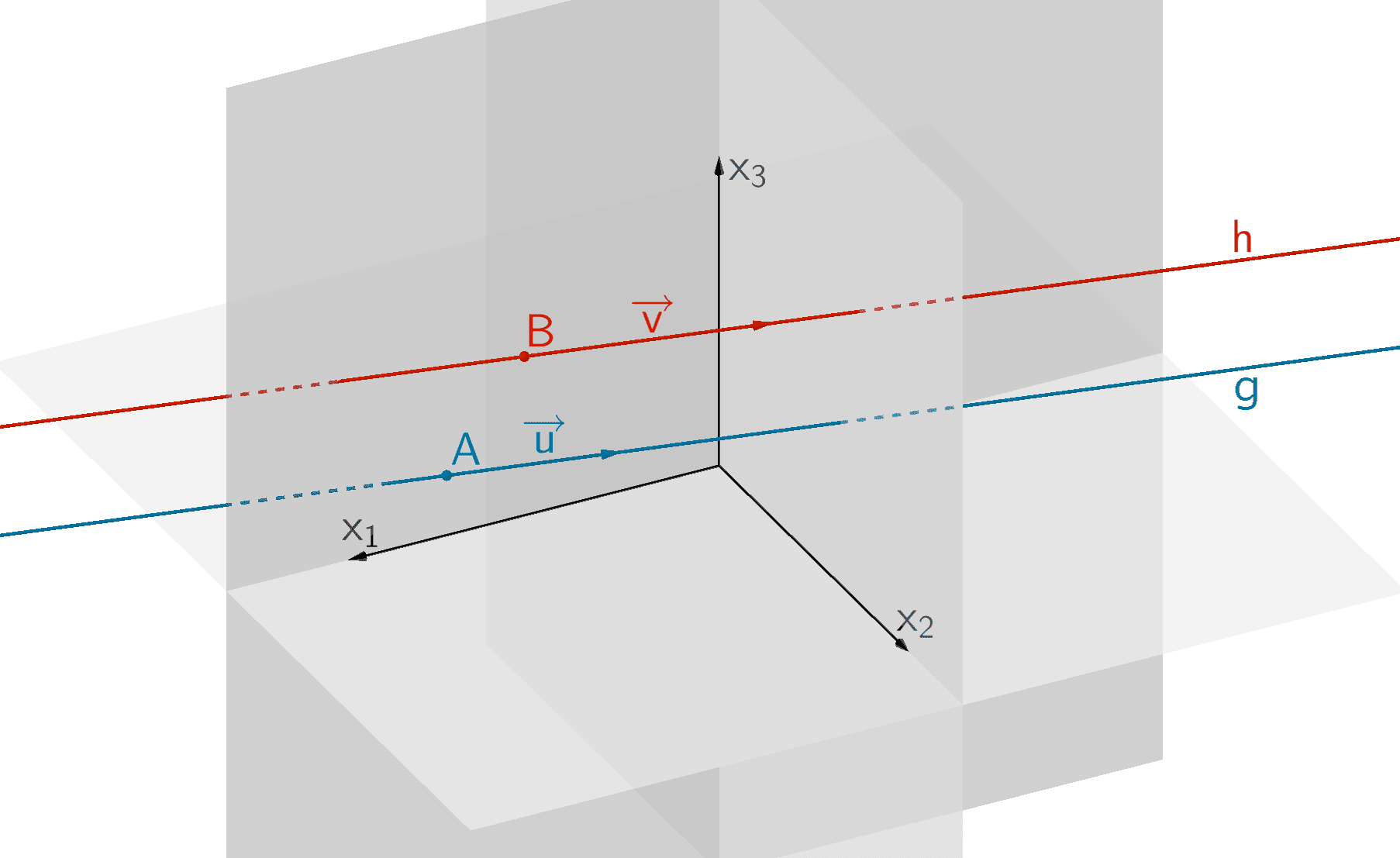
Die Geraden \(g\) und \(h\) sind (echt) parallel.
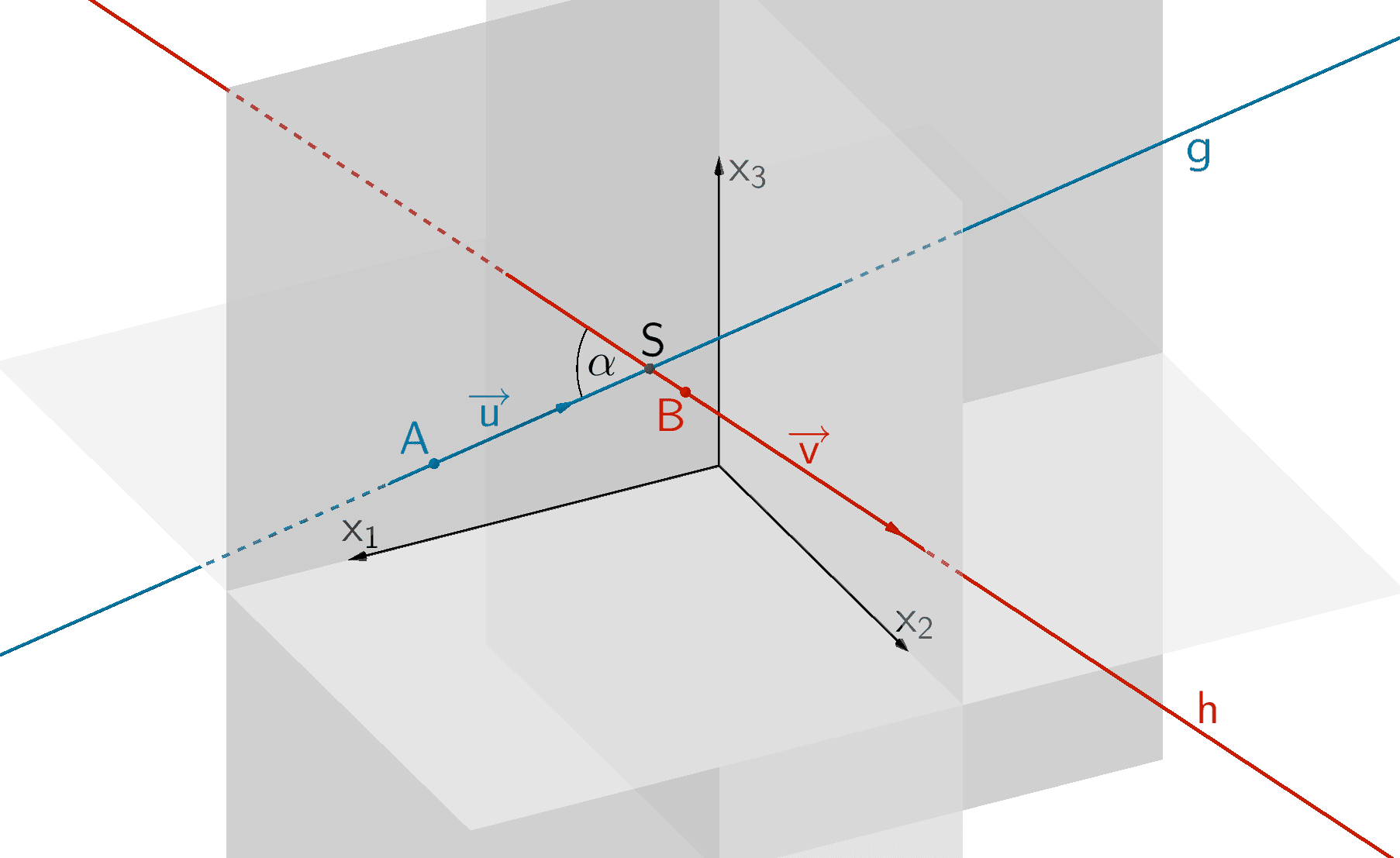
Die Geraden \(g\) und \(h\) schneiden sich in einem Schnittpunkt \(S\) unter dem Schnittwinkel \(\alpha\).
Die Geraden \(g\) und \(h\) verlaufen windschief zueinander.
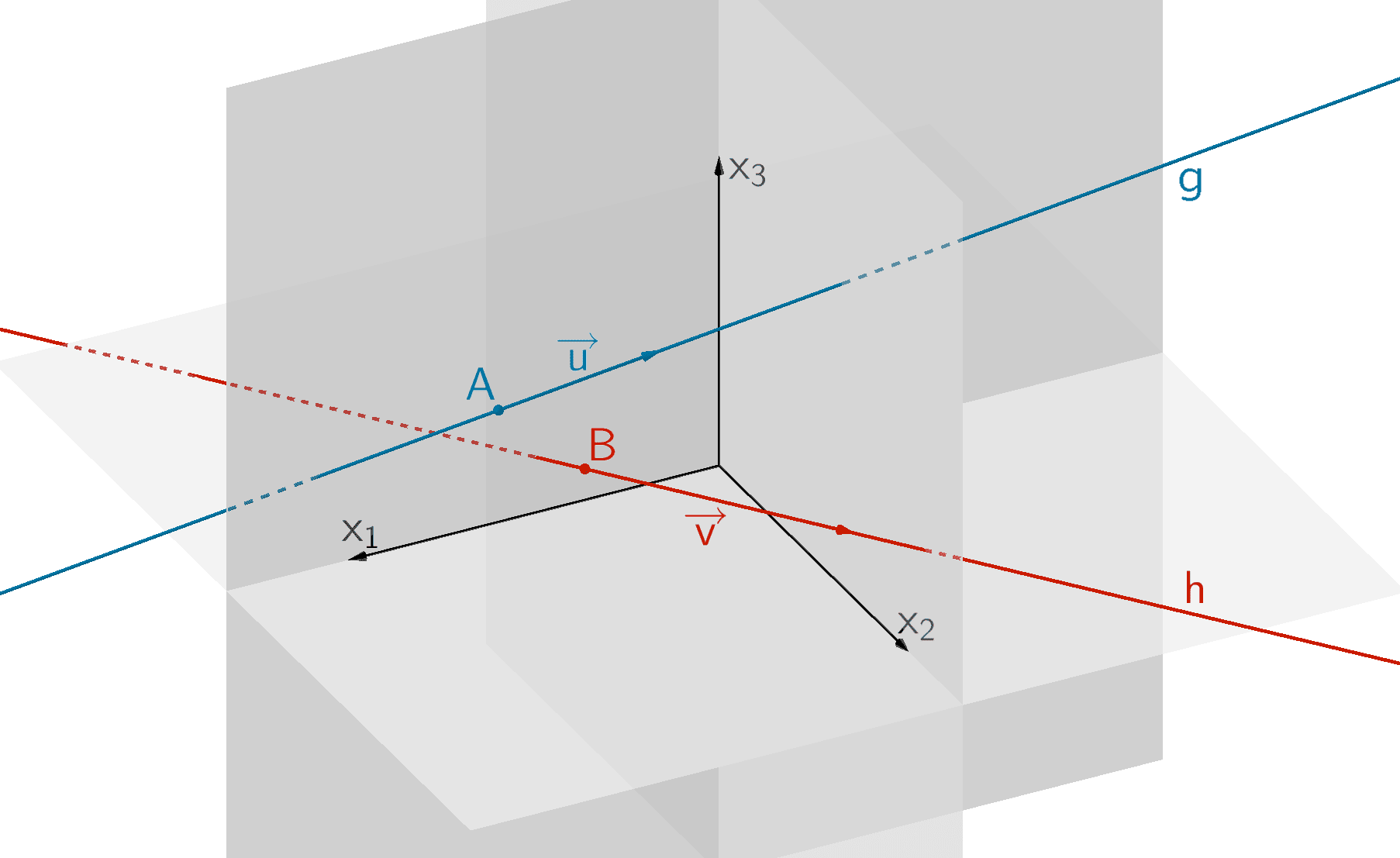
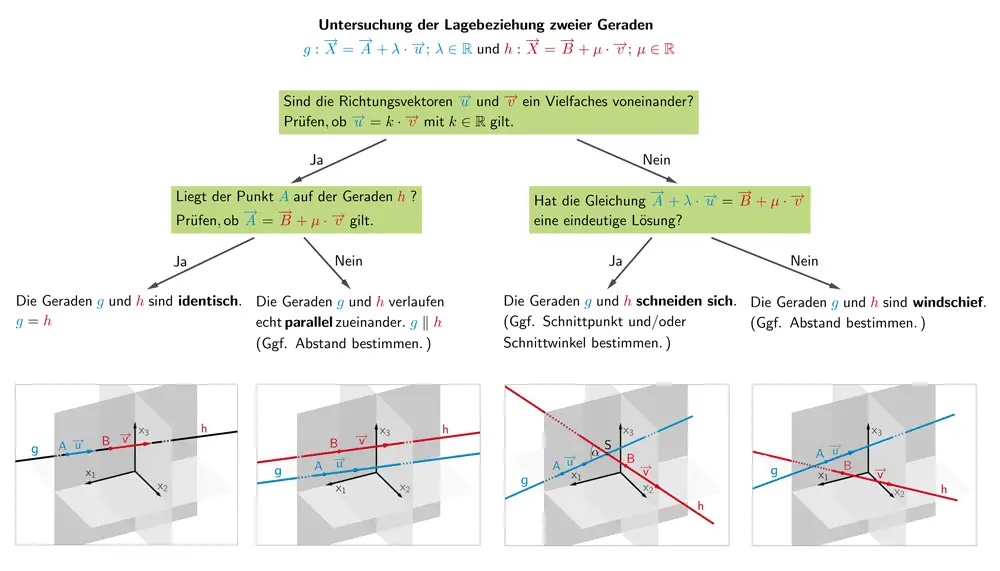
Untersuchung der Lagebeziehung zweier Geraden
Für die Untersuchung der gegenseitigen Lage zweier Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \enspace \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \enspace \mu \in \mathbb R\) betrachtet man die Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der Geradengleichungen.
![]() Untersuchung der Lagebeziehung zweier Geraden
Untersuchung der Lagebeziehung zweier Geraden
Man überprüft zuerst die Lineare (Un-)Abhängigkeit der Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).
Gilt \(\overrightarrow{u} = k \cdot \overrightarrow{v}\,, \; k \in \mathbb R\), sind \(\overrightarrow{u}\) und \(\overrightarrow{v}\) linear abhängig und damit parallel. Die Geraden \(g\) und \(h\) können dann identisch sein oder (echt) parallel zueinander verlaufen. Erfüllt ein Aufpunkt der einen Geradengleichung die Gleichung der anderen Geraden (Punktprobe), sind die Geraden \(g\) und \(h\) identisch. Andernfalls sind die Geraden (echt) parallel.
Gilt \(\overrightarrow{u} \neq k \cdot \overrightarrow{v}\,, \;k \in \mathbb R\), sind \(\overrightarrow{u}\) und \(\overrightarrow{v}\) linear unabhängig und damit nicht parallel. Nun prüft man, ob die Geraden \(g\) und \(h\) sich in einem Punkt schneiden (vgl. Berechnung des Schnittpunkts zweier Geraden). Ist dies nicht der Fall, verlaufen die Geraden in einem Abstand windschief zueinander (vgl. Abiturskript - 2.4.3 Abstand windschiefer Geraden).
Berechnung des Schnittpunkts zweier Geraden
Für die Berechnung des Schnittpunkts zweier Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \enspace \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \enspace \mu \in \mathbb R\) werden die Ortsvektoren \(\overrightarrow{X}_{g}\) und \(\overrightarrow{X}_{h}\) der Geradengleichungen von \(g\) und \(h\) gleichgesetzt.
\[\begin{align*} \overrightarrow{X}_{g} &= \overrightarrow{X}_{h} \\[0.8em] \overrightarrow{A} + \lambda \cdot \overrightarrow{u} &= \overrightarrow{B} + \mu \cdot \overrightarrow{v} \\[0.8em] \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} + \lambda \cdot \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix} &= \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} + \mu \cdot \begin{pmatrix} v_{1} \\ v_{2} \\ v_{3} \end{pmatrix} \end{align*}\]
Daraus ergibt sich ein lineares Gleichungssystem mit drei Gleichungen und den beiden Unbekannten \(\lambda\) und \(\mu\).
\[\begin{align*} \text{I} & & & a_{1} + \lambda \cdot u_{1} = b_{1} + \mu \cdot v_{1} \\[0.8em] \text{II} & & \wedge \enspace &a_{2} + \lambda \cdot u_{2} = b_{2} + \mu \cdot v_{2} \\[0.8em] \text{III} & & \wedge \enspace &a_{3} + \lambda \cdot u_{3} = b_{3} + \mu \cdot v_{1} \end{align*}\]
Zwei Gleichungen werden zur Bestimmung der Werte für \(\lambda\) und \(\mu\) verwendet. Anhand der dritten Gleichung führt man die Probe durch. Die Lösung ist nur dann eindeutig, wenn die ermittelten Werte für \(\lambda\) und \(\mu\) die dritte Gleichung erfüllen (wahre Aussage).
Im Falle einer eindeutigen Lösung für \(\lambda\) und \(\mu\) erhält man den Ortsvektor des Schnittpunkts \(S\) der Geraden \(g\) und \(h\), indem man entweder den ermittelten Wert für \(\lambda\) in die Geradengleichung \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) einsetzt oder den ermittelten Wert für \(\mu\) in die Geradengleichung \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\) einsetzt.
Beispiel:
Bestimmen Sie den Schnittpunkt \(S\) der Geraden \(g \colon \overrightarrow{X} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} + \mu \cdot \begin{pmatrix} 4 \\ 3 \\ -6 \end{pmatrix}; \; \mu \in \mathbb R\).
Ortsvektoren \(\overrightarrow{X}_{g}\) und \(\overrightarrow{X}_{h}\) der Geraden \(g\) und \(h\) gleichsetzen:
\[\begin{align*} \overrightarrow{X}_{g} &= \overrightarrow{X}_{h} \\[0.8em] \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} &= \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} + \mu \cdot \begin{pmatrix} 4 \\ 3 \\ -6 \end{pmatrix} \end{align*}\]
Lineares Gleichungssystem formulieren:
\[\begin{align*} \text{I} & & & 1 + 3\lambda = -5 + 4\mu \\[0.8em] \text{II} & & \wedge \enspace & 2 + 3\lambda = -3 + 3\mu \\[0.8em] \text{III} & & \wedge \enspace & 3 + 3\lambda = \enspace \; 7 - 6\mu \end{align*}\]
Lineares Gleichungssystem lösen:
Das lineare Gleichungssystem lässt sich beispielsweise mit dem Additionsverfahren (bzw. Subtraktion) lösen. Der Rechenschritt \(\text{I} - \text{II}\) „eliminiert" den Summanden \(3\lambda\) und man erhält eine Gleichung für \(\mu\).
\[\begin{align*}\text{I} - \text{II} \colon \; 1 - 2 + 3\lambda - 3\lambda &= -5 - (-3) + 4\mu - 3\mu \\[0.8em] -1 &= -2 + \mu & &| + 2 \\[0.8em] 1 &= \mu \end{align*}\]
\[\begin{align*}\mu = 1 \; \text{in I} \colon \; 1 + 3\lambda &= -5 + 4 \cdot 1 \\[0.8em] 1 + 3\lambda &= -1 & &| - 1 \\[0.8em] 3\lambda &= -2 & &| : 3 \\[0.8em] \lambda &= -\frac{2}{3}\end{align*}\]
Probe mit der noch nicht verwendeten dritten Gleichung:
\[\begin{align*} \lambda = -\frac{2}{3}, \mu = 1 \; \text{in III} \colon \; 3 + 3 \cdot \left( -\frac{2}{3} \right) &= 7 - 6 \cdot 1 \\[0.8em] 1 &= 1 \quad (\text{w}) \end{align*}\]
\(\Longrightarrow \quad\)Eindeutige Lösung: \(\lambda = -\dfrac{2}{3}\), \(\mu = 1\)
Koordinaten des Schnittpunkts \(S\) berechnen:
Für die Berechnung der Koordinaten des Schnittpunkts \(S\) der Geraden \(g\) und \(h\) wird beispielsweise der ermittelte Parameterwert \(\mu = 1\) in die Gleichung der geraden \(h\) eingesetzt.
\[h \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} + \mu \cdot \begin{pmatrix} 4 \\ 3 \\ -6 \end{pmatrix}; \; \mu \in \mathbb R\]
\[S \in h \colon \overrightarrow{S} = \begin{pmatrix} -5 \\ -3 \\ 7 \end{pmatrix} + 1 \cdot \begin{pmatrix} 4 \\ 3 \\ -6 \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad S(-1|0|1)\]
Beispielaufgabe
Gegeben seien die Geraden
\(g \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\),
\(h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} -10 \\ -5 \\ 6 \end{pmatrix}; \; \mu \in \mathbb R\) und
\(k \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -2 \\ 0 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ -1 \\ -\frac{2}{3} \end{pmatrix}; \; \tau \in \mathbb R\).
Untersuchen Sie die gegenseitige Lage der Geraden \(g\) und \(h\) sowie der Geraden \(g\) und \(k\).
Lagebeziehung der Geraden \(g\) und \(h\)
\[g \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} -10 \\ -5 \\ 6 \end{pmatrix}; \; \mu \in \mathbb R\]
Richtungsvektoren auf Lineare (Un-)Abhängigkeit überprüfen:
\[\begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix} = k \cdot \begin{pmatrix} -10 \\ -5 \\ 6 \end{pmatrix}; \; k \in \mathbb R \enspace \Longrightarrow \enspace \left\{ \begin{align*} -3 = -10k \enspace &\Longrightarrow \enspace k = \enspace \; \frac{3}{10} \\[0.8em] \enspace \; 3 = \enspace -5k \enspace &\Longrightarrow \enspace k = -\frac{3}{5} \\[0.8em] \enspace \; 2 = \quad \; 6k \enspace &\Longrightarrow \enspace k = \enspace \; \frac{1}{3} \end{align*} \right\} \enspace \Large{\text{↯}}\]
\[\Longrightarrow \quad \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix} \neq k \cdot \begin{pmatrix} -10 \\ -5 \\ 6 \end{pmatrix}; \; k \in \mathbb R\]
Die Richtungsvektoren der Geraden \(g\) und \(h\) sind linear unabhängig. Folglich können sich die Geraden \(g\) und \(h\) in einem Punkt schneiden oder windschief zueinander verlaufen.
Prüfen, ob sich die Geraden \(g\) und \(h\) schneiden:
Die Ortsvektoren \(\overrightarrow{X}_{g}\) und \(\overrightarrow{X}_{h}\) der Geraden \(g\) und \(h\) werden gleichgesetzt.
\[\begin{align*} \overrightarrow{X}_{g} &= \overrightarrow{X}_{h} \\[0.8em] \begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix} &= \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} -10 \\ -5 \\ 6 \end{pmatrix} \end{align*}\]
Lineares Gleichungssystem formulieren:
\[\begin{align*} \text{I} & & & \quad \;5 - 3\lambda = \enspace \; 6 - 10\mu \\[0.8em] \text{II} & & \wedge \enspace & -5 + 3\lambda = \enspace \; 3 - \enspace 5\mu \\[0.8em] \text{III} & & \wedge \enspace & -2 + 2\lambda = -3 + \enspace 6\mu \end{align*}\]
Lineares Gleichungssystem lösen:
Das lineare Gleichungssystem lässt sich beispielsweise mit dem Additionsverfahren lösen. Der Rechenschritt \(\text{I} + \text{II}\) „eliminiert" den Summanden \(3\lambda\) und man erhält eine Gleichung für \(\mu\).
\[\begin{align*} \text{I} + \text{II} \colon \; 5 - 5 - 3\lambda + 3\lambda &= 6 + 3 - 10\mu - 5\mu \\[0.8em] 0 &= 9 - 15\mu & &| + 15\mu \\[0.8em] 15\mu &= 9 & &| : 15 \\[0.8em] \mu &= \frac{9}{15} \\[0.8em] \mu &= \frac{3}{5} \end{align*}\]
\[\begin{align*} \mu = \frac{3}{5} \; \text{in II} \colon \; -5 + 3\lambda &= 3 - 5 \cdot \frac{3}{5} \\[0.8em] -5 + 3\lambda &= 0 & &| + 5 \\[0.8em] 3\lambda &= 5 & &| : 3 \\[0.8em] \lambda &= \frac{5}{3} \end{align*}\]
Probe mit der noch nicht verwendeten dritten Gleichung:
\[\begin{align*} \lambda = \frac{5}{3}\,, \; \mu = \frac{3}{5} \; \text{in III} \colon \; -2 + 2 \cdot \frac{5}{3} &= -3 + 6 \cdot \frac{3}{5} \\[0.8em] -\frac{6}{3} + \frac{10}{3} &= -\frac{15}{5} + \frac{18}{5} \\[0.8em] \frac{4}{3} &= \frac{3}{5} \quad (\text{f}) \end{align*}\]
\(\Longrightarrow \quad\)keine eindeutige Lösung für \(\lambda\) und \(\mu\)
\(\Longrightarrow \quad\)Die Geraden \(g\) und \(h\) sind windschief (vgl. Abiturskript - 2.4.3 Abstand windschiefer Geraden).
Lagebeziehung der Geraden \(g\) und \(k\)
\[g \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[k \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -2 \\ 0 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ -1 \\ -\frac{2}{3} \end{pmatrix}; \; \tau \in \mathbb R\]
Richtungsvektoren auf Lineare (Un-)Abhängigkeit überprüfen:
\[\begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix} = k \cdot \begin{pmatrix} 1 \\ -1 \\ -\frac{2}{3} \end{pmatrix}; \; k \in \mathbb R \enspace \Longrightarrow \enspace \left\{ \begin{align*} -3 = \quad \enspace \; k \enspace &\Longrightarrow \enspace k = -3 \\[0.8em] \enspace \; 3 = \quad -k \enspace &\Longrightarrow \enspace k = -3 \\[0.8em] \enspace \; 2 = -\frac{2}{3}k \enspace &\Longrightarrow \enspace k = -3 \end{align*} \right. \]
\[\Longrightarrow \quad \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix} = (-3) \cdot \begin{pmatrix} 1 \\ -1 \\ -\frac{2}{3} \end{pmatrix} \quad \Longrightarrow \quad \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix} \parallel \begin{pmatrix} 1 \\ -1 \\ -\frac{2}{3} \end{pmatrix}\]
Die Richtungsvektoren der Geraden \(g\) und \(k\) sind linear abhängig. Folglich können die Geraden \(g\) und \(k\) (echt) parallel oder identisch sein.
Prüfen, ob die Geraden \(g\) und \(k\) identisch sind:
Mithilfe der Punktprobe prüft man, ob die Geraden \(g\) und \(k\) identisch sind. Das heißt, man überprüft, ob der Ortsvektor eines beliebigen bekannten Punktes der Geraden \(g\) die Geradengleichung von \(k\) erfüllt oder umgekehrt. Praktischerweise verwendet man hierfür den bereits bekannten Ortsvektor eines Aufpunkts.
\[g \colon \overrightarrow{X} = \begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[k \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -2 \\ 0 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ -1 \\ -\frac{2}{3} \end{pmatrix}; \; \tau \in \mathbb R\]
\[\begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} \text{in k} \colon \, \begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \\ 0 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ -1 \\ -\frac{2}{3} \end{pmatrix}\]
\[\Longrightarrow \enspace \left\{ \begin{align*} \enspace \; 5 = \enspace \; 2 + \enspace \tau \enspace &\Longrightarrow \enspace \tau = 3 \\[0.8em] -5 = -2 - \enspace \tau \enspace &\Longrightarrow \enspace \tau = 3 \\[0.8em] -2 = \quad \; -\frac{2}{3}\tau \enspace &\Longrightarrow \enspace \tau = 3 \end{align*} \right\} \enspace \Longrightarrow \enspace g, k \; \text{identisch}\]
oder
\[\begin{pmatrix} 2 \\ -2 \\ 0 \end{pmatrix} \text{in g} \colon \, \begin{pmatrix} 2 \\ -2 \\ 0 \end{pmatrix} = \begin{pmatrix} 5 \\ -5 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 3 \\ 2 \end{pmatrix}\]
\[\Longrightarrow \enspace \left\{ \begin{align*} \enspace \; 2 = \enspace \; 5 - 3\lambda \enspace &\Longrightarrow \enspace \lambda = 1 \\[0.8em] -2 = -5 + 3\lambda \enspace &\Longrightarrow \enspace \lambda = 1 \\[0.8em] \enspace \; 0 = -2 + 2\lambda \enspace &\Longrightarrow \enspace \lambda = 1 \end{align*} \right\} \enspace \Longrightarrow \enspace g, k \; \text{identisch}\]