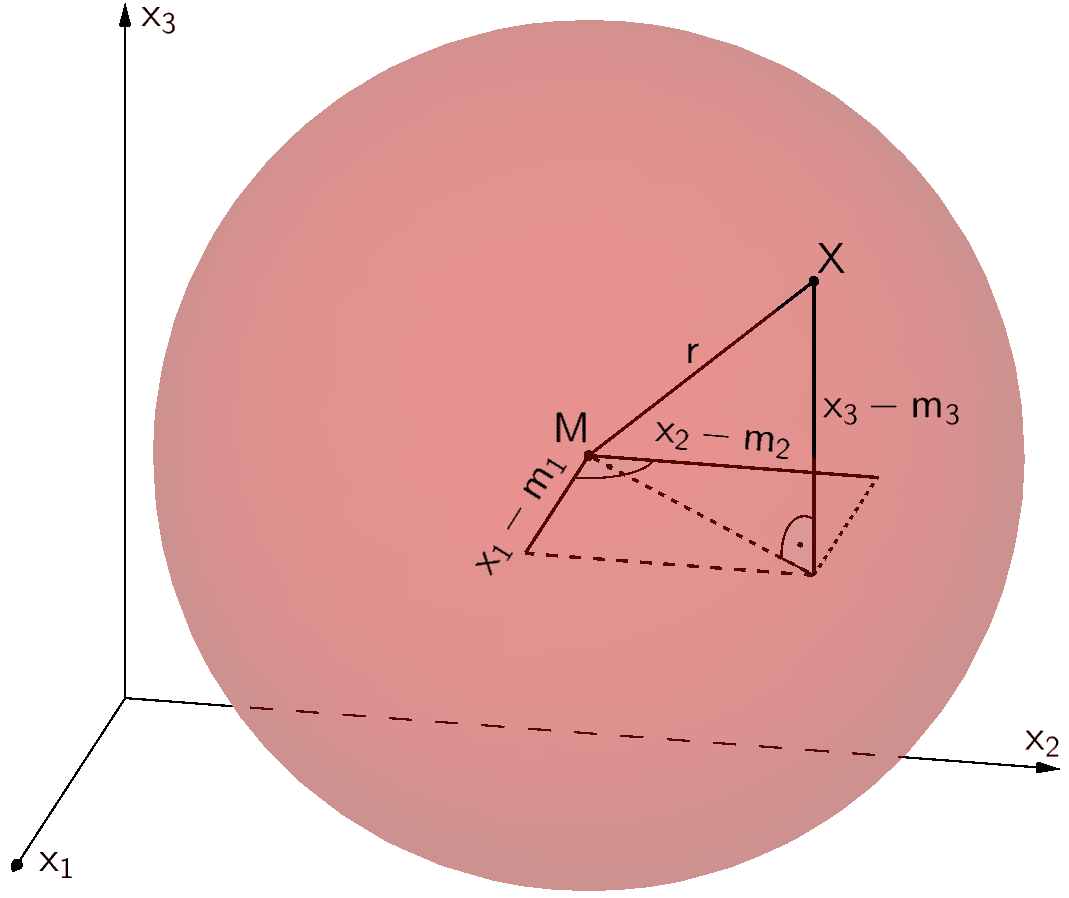
Eine Kugel ist die Menge aller Punkte \(X\) im Raum, die von einem festen Punkt \(M\) (Mittelpunkt) den gleichen Abstand \(r\) (Radius) haben.
\[\overline{MX} = \vert \overrightarrow{MX} \vert = r\]
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
Beispielaufgabe
Der Punkt \(P(3|-2|0)\) liegt auf der Kugel \(K\) mit dem Mittelpunkt \(M(-1|2|2)\).
Berechnen Sie den Radius \(r\) der Kugel \(K\) und geben Sie die Gleichung der Kugel in Vektor- und Koordinatendarstellung an.
Radius \(r\) der Kugel \(K\)
\(M(-1|2|2)\), \(P(3|-2|0)\)
De Ansatz kann über die Vektordarstellung oder die Koordinatendarstellung erfolgen.
Vektordarstelliung:
\[\begin{align*} K \colon (\overrightarrow{X} - \overrightarrow{M})^{2} &= r^{2} \\[0.8em] P \in K \colon (\overrightarrow{P} - \overrightarrow{M})^{2} &= r^{2} \\[0.8em] \left[ \begin{pmatrix} 3 \\ -2 \\ 0 \end{pmatrix} - \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix} \right]^{2} &= r^{2} \\[0.8em] \left[\begin{pmatrix} 4 \\ -4 \\ -2 \end{pmatrix} \right]^{2} &= r^{2} \\[0.8em] 4^{2} + (-4)^{2} + (-2)^{2} &= r^{2} \\[0.8em] 36 &= r^{2} \\[0.8em] 6 &= r \end{align*}\]
Koordinatendarstellung:
\[\begin{align*} K \colon (x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{3} &= r^{2} \\[0.8em] P \in K \colon (p_{1} - m_{1})^{2} + (p_{2} - m_{2})^{2} + (p_{3} - m_{3})^{3} &= r^{2} \\[0.8em] (3 - (-1))^{2} + (-2 - 2)^{2} + (0 - 2)^{2} &= r^{2} \\[0.8em] 4^{2} + (-4)^{2} + (-2)^{2} &= r^{2} \\[0.8em] 36 &= r^{2} \\[0.8em] 6 &= r \end{align*}\]
Kugelgleichung in Vektor- und Koordinatendarstellung
\(M(-1|2|2)\), \(r = 6\)
Vektordarstellung:
\[\begin{align*} &K \colon (\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2} \\[0.8em] &K \colon \left[\overrightarrow{X} - \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix} \right]^{2} = 6^{2} \end{align*}\]
Koordinatendarstellung:
\[\begin{align*} &K \colon (x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2} \\[0.8em] &K \colon (x_{1} + 1)^{2} + (x_{2} - 2)^{2} + (x_{3} - 2)^{2} = 6^{2} \end{align*}\]

