Geben Sie jeweils eine Gleichung der Gerade \(g\) an, für die gilt:
a) Die Gerade \(g\) ist eine Ursprungsgerade und der Punkt \(P(1|3|4)\) liegt auf \(g\).
b) Die Gerade \(g\) verläuft parallel zur \(x_{2}\)-Achse durch den Punkt \(Q(-2|2|0)\).
c) Die Gerade \(g\) verläuft parallel zur \(x_{1}x_{3}\)-Ebene durch den Punkt \(R(-2{,}5|1|1)\).
d) Die Gerade \(g\) verläuft durch die Punkte \(S(3|2|-1)\) und \(T(6|4|0)\).
a) Die Gerade \(g\) ist eine Ursprungsgerade und der Punkt \(P(1|3|4)\) liegt auf \(g\)
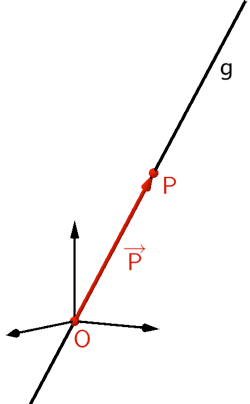
Der Koordinatenursprung \(O(0|0|0)\) dient als Aufpunkt und der Ortsvektor \(\overrightarrow{P}\) ist ein Richtungsvektor der Gleichung der Geraden \(g\) in Parameterform (vgl. Abiturskript - 2.2.1 Geradengleichung in Parameterform, Lage einer Geraden im Koordinatensystem).
\[O(0|0|0),P(1|3|4) \in g\]
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} g \colon \overrightarrow{X} &= \overrightarrow{O} + \lambda \cdot \overrightarrow{P}; \; \lambda \in \mathbb R \\[0.8em] g \colon \overrightarrow{X} &= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 3 \\ 4 \end{pmatrix} = \lambda \cdot \begin{pmatrix} 1 \\ 3 \\ 4 \end{pmatrix}; \; \lambda \in \mathbb R \end{align*}\]
b) Die Gerade \(g\) verläuft parallel zur \(x_{2}\)-Achse durch den Punkt \(Q(-2|2|0)\)
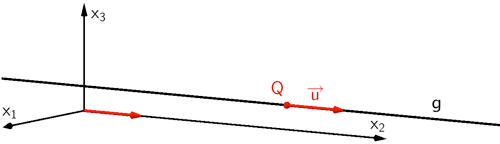
Der Punkt \(Q\) dient als Aufpunkt und der Vektor \(\overrightarrow{u} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\) ist beispielsweise ein Richtungsvektor der Gleichung der Geraden \(g\) in Parameterform (vgl. Abiturskript - 2.2.1 Geradengleichung in Parameterform, Lage einer Geraden im Koordinatensystem).
\(Q(-2|2|0) \in g\), \(g \parallel x_{2}\)-Achse
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} g \colon \overrightarrow{X} &= \overrightarrow{Q} + \mu \cdot \overrightarrow{u}; \; \mu \in \mathbb R \\[0.8em] g \colon \overrightarrow{X} &= \begin{pmatrix} -2 \\ 2 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R \end{align*}\]
c) Die Gerade \(g\) verläuft parallel zur \(x_{1}x_{3}\)-Ebene durch den Punkt \(R(-2{,}5|1|1)\)
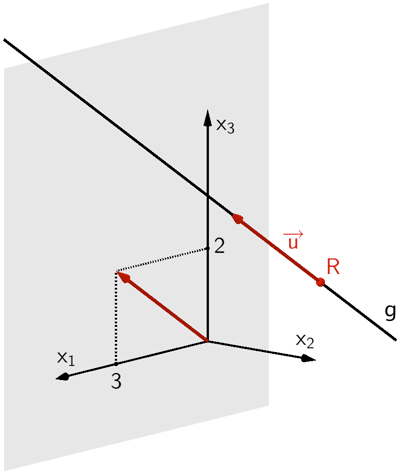
Der Punkt \(R\) dient als Aufpunkt und der Vektor \(\overrightarrow{u} = \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix}\) ist beispielsweise ein Richtungsvektor der Gleichung der Geraden \(g\) in Parameterform (vgl. Abiturskript - 2.2.1 Geradengleichung in Parameterform, Lage einer Geraden im Koordinatensystem).
\(R(-2{,}5|1|1) \in g\), \(g \parallel x_{1}x_{3}\)-Ebene
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} g \colon \overrightarrow{X} &= \overrightarrow{R} + \sigma \cdot \overrightarrow{u}; \; \sigma \in \mathbb R \\[0.8em] g \colon \overrightarrow{X} &= \begin{pmatrix} -2{,}5 \\ 1 \\ 1 \end{pmatrix} + \sigma \cdot \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix}; \; \sigma \in \mathbb R \end{align*}\]
d) Die Gerade \(g\) verläuft durch die Punkte \(S(3|2|-1)\) und \(T(6|4|0)\)
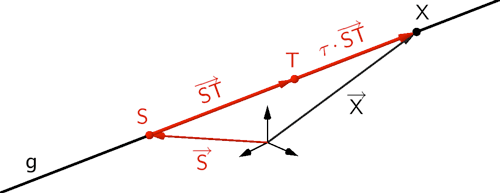
Beispielsweise dient der Punkt \(S\) als Aufpunkt und der Verbindungsvektor \(\overrightarrow{ST}\) ist ein Richtungsvektor der Gleichung der Geraden \(g\) in Parameterform (vgl. Abiturskript - 2.2.1 Geradengleichung in Parameterform).
\(S(3|2|-1)\), \(T(6|4|0) \in g\)
Verbindungsvektor \(\overrightarrow{ST}\) berechnen:
\[\overrightarrow{ST} = \overrightarrow{T} - \overrightarrow{S} = \begin{pmatrix} 6 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}\]
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} g \colon \overrightarrow{X} &= \overrightarrow{S} + \tau \cdot \overrightarrow{ST}; \; \tau \in \mathbb R \\[0.8em] g \colon \overrightarrow{X} &= \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix} + \tau \cdot \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}; \; \tau \in \mathbb R \end{align*}\]

