Lösung zu Teilaufgabe d
Neigungswinkel der Seitenkante \([BS]\) gegen die Ebene \(E\)
Der Neigungswinkel der Seitenkante \([BS]\) gegen die Ebene \(E\) entspricht dem Schnittwinkel \(\alpha\) zwischen der Geraden \(BS\), und der Ebene \(E\).
Schnittwinkel zwischen Gerade und Ebene
Schnittwinkel \(\boldsymbol{\alpha}\) zwischen Gerade und Ebene
Für \(0^{\circ} \leq \alpha \leq 90^{\circ}\) und \(0^{\circ} \leq \beta \leq 90^{\circ}\) gilt:
\[\begin{align*} \cos \beta &= \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \enspace \Rightarrow \enspace \beta = \cos^{-1}(\dots) \\[0.8em] \alpha &= 90^{\circ} - \beta \end{align*}\]
\[\sin \alpha = \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \enspace \Rightarrow \enspace \alpha = \sin^{-1}(\dots)\]
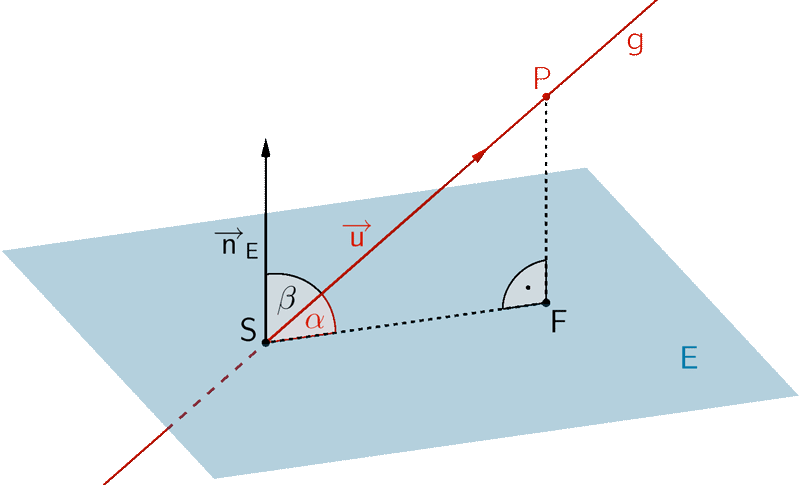
Richtungsvektor \(\overrightarrow {u}_g\) der Geraden \(g\):
\[\overrightarrow {u}_g = \overrightarrow{BS} = \overrightarrow S - \overrightarrow B = \begin {pmatrix} 11{,}5 \\ 4 \\ -6 \end {pmatrix} - \begin {pmatrix} 6 \\ -7 \\ 1 \end {pmatrix} = \begin {pmatrix} 5{,}5 \\ 11 \\ -7 \end {pmatrix}\]
Normalenvektor \(\overrightarrow {n}_E\) der Ebene \(E\):
Aus Teilaufgabe c ist bekannt: \(\overrightarrow {n}_E = \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix}\).
Berechnung des Schnittwinkels \(\alpha\):
Betrag eines Vektors
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
Skalarprodukt
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \sin \alpha &= \frac{\vert \overrightarrow u \circ \overrightarrow {n}_E \vert}{\vert \overrightarrow u \vert \cdot \vert \overrightarrow {n}_E \vert} \\[0.8em] &= \frac{\left|\begin {pmatrix} 5{,}5 \\ 11 \\ -7 \end {pmatrix} \circ \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix}\right|}{\left| \begin {pmatrix} 5{,}5 \\ 11 \\ -7 \end {pmatrix} \right| \cdot \left| \begin {pmatrix} 2 \\ 1 \\ -2 \end {pmatrix} \right|} \\[0.8em] &= \frac{\vert|5{,}5 \cdot 2 + 11 \cdot 1 + (-7) \cdot (-2)\vert}{\sqrt{5{,}5^2 + 11^2 + (-7)^2} \cdot \sqrt{2^2 + 1^2 + (-2)^2}} \\[0.8em] &= 0{,}847 \dots & &| \sin^{-1}(\dots) \\[0.8em] \alpha &\approx 58^{\circ} \end{align*}\]
Der Neigungswinkel der Seitenkante \([BS]\) gegen die Ebene \(E\) beträgt ca. 58°.
Veranschaulichung: Neigungswinkel der Seitenkante \([BS]\) gegen die Ebene \(E\)
Das Lot des Punktes \(S\) auf die Ebene \(E\) legt den Lotfußpunkt \(F\) fest. Der Neigungswinkel \(\alpha\) der Seitenkante \([BS]\) gegen die Ebene \(E\) ist definiert als der Winkel \(SBF\) im rechtwinkligen Dreieck \(BSF\,\). Im vorliegenden Fall liegt der Lotfußpunkt \(F\) auf der Seitenkante \([AB]\) und der Neigungswinkel \(\alpha\) ist gleich dem Winkel, den die Seitenkannten \([BS]\) und \([AB]\) einschließen.
Volumen \(V\) der Pyramide
1. Lösungsansatz: Anwenden des Spatprodukts
Spatprodukt
Anwendung des Vekorprodukts - Spatprodukt (vgl. Merkhilfe)
Volumen eines Spats
\[V_{\text{Spat}} = \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
Volumen einer dreiseitigen Pyramide
\[V_{\text{Pyramide}} = \frac{1}{6} \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
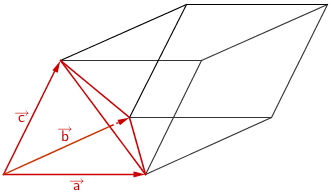
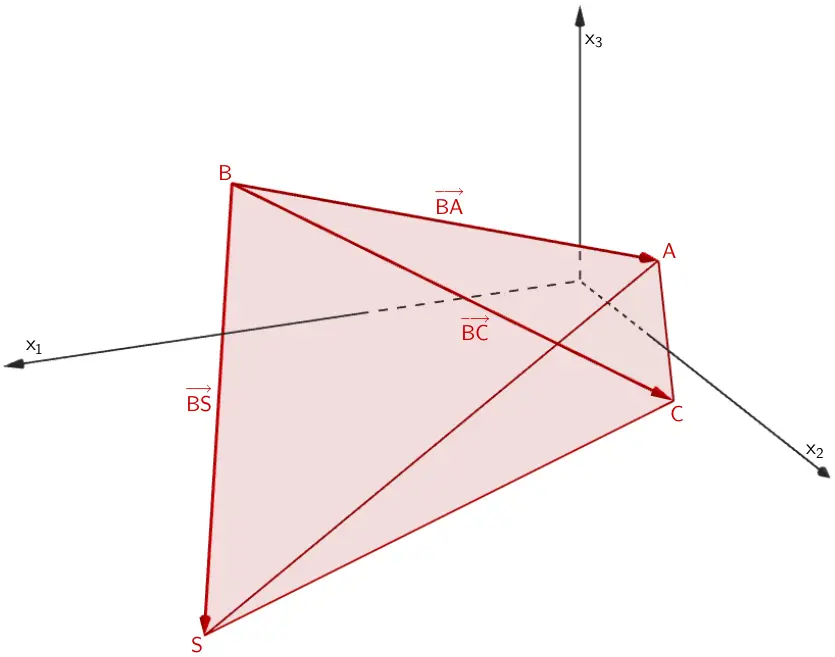
Das Volumen \(V\) der Pyramide lässt sich durch Anwenden des Spatprodukts berechnen. Dazu wählt man beispielsweise die drei linear unabhängigen Vektoren \(\overrightarrow{BA}\,,\;\overrightarrow{BC}\) und \(\overrightarrow{BS}\).
\[V_{ABCS} = \frac{1}{6} \cdot \left| \left( \overrightarrow{BA} \times \overrightarrow{BC} \right) \circ \overrightarrow{BS}\;\right|\]
\[\overrightarrow{BA} = \overrightarrow A - \overrightarrow B = \begin {pmatrix} 1 \\ 7 \\ 3 \end {pmatrix} - \begin {pmatrix} 6 \\ -7 \\ 1 \end {pmatrix} = \begin {pmatrix} -5 \\ 14 \\ 2 \end {pmatrix}\]
\[\overrightarrow{BC} = \overrightarrow C - \overrightarrow B = \begin {pmatrix} -2 \\ 1 \\ -3 \end {pmatrix} - \begin {pmatrix} 6 \\ -7 \\ 1 \end {pmatrix} = \begin {pmatrix} -8 \\ 8 \\ -4 \end {pmatrix}\]
\(\overrightarrow{BS} = \begin {pmatrix} 5{,}5 \\ 11 \\ -7 \end {pmatrix}\) (siehe oben)
Vektorprodukt
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
Skalarprodukt
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[ \begin {align*} V_{ABCS} &= \frac{1}{6} \cdot \left| \left( \overrightarrow{BA} \times \overrightarrow{BC} \right) \circ \overrightarrow{BS}\;\right| \\[0.8em] &= \frac{1}{6} \cdot \left| \left[ \begin {pmatrix} -5 \\ 14 \\ 2 \end {pmatrix} \times \begin {pmatrix} -8 \\ 8 \\ -4 \end {pmatrix} \right] \circ \begin {pmatrix} 5{,}5 \\ 11 \\ -7 \end {pmatrix} \right| \\[0.8em] &= \frac{1}{6} \cdot \left| \begin {pmatrix} 14 & \cdot & (-4) & - & 2 & \cdot & 8 \\ 2 & \cdot & (-8) & - & (-5) & \cdot & (-4) \\ (-5) & \cdot & 8 & - & 14 & \cdot & (-8) \end {pmatrix} \circ \begin {pmatrix} 5{,}5 \\ 11 \\ -7 \end {pmatrix} \right| \\[0.8em] &= \frac{1}{6} \cdot \left| \begin {pmatrix} -72 \\ -36 \\ 72 \end {pmatrix} \circ \begin {pmatrix} 5{,}5 \\ 11 \\ -7 \end {pmatrix} \right| \\[0.8em] &= \frac{1}{6} \cdot \left| (-72) \cdot 5{,}5 + (-36) \cdot 11 + 72 \cdot (-7) \right| \\[0.8em] &= \frac{1}{6} \cdot \left| -1296 \right| \\[0.8em] &= 216 \end {align*} \]
Das Volumen \(V_{ABCS}\) der Pyramide \(ABCS\) beträgt \(216\) VE (Volumeneinheiten).
2. Lösungsansatz: Höhe der Pyramide bestimmen
Die Höhe der Pyramide \(ABCS\) ist gleich dem Abstand der Spitze \(S\) von der Grundfläche \(ABC\), welche die Ebene \(E\) festlegt (siehe Teilaufgabe c).
Volumen einer Pyramide
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
(vgl. Merkhilfe)
\[V = \frac{1}{3} \cdot A_{ABC} \cdot h\,; \quad h = d\,(S;E)\]
Höhe \(h\) der Pyramide \(ABCS\) bestimmen:
Abstand Punkt - Ebene
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\(E \colon \enspace 2x_1 + x_2 -2 x_3 - 3 = 0\;\) (siehe Teilaufgabe c)
\[\overrightarrow{n}_E = \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}\]
Betrag eines Vektors
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\vert \overrightarrow{n}_E \vert = \left| \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} \right| = \sqrt{2^2 + 1^2 + (-2)^2} = 3\]
\[E^{HNF} \colon \enspace \frac{2x_1 + x_2 - 2x_3}{3} = 0\]
Abstand \(d\,(S;E)\) berechnen:
\[S\,(11{,}5|4|-6)\]
\[d\,(S;E) = \left| \frac{2s_1 + s_2 - 2s_3 - 3}{3} \right| = \left| \frac{2 \cdot 11{,}5 + 4 - 2 \cdot (-6) - 3}{3} \right| = 12\]
\[\Longrightarrow \quad h = 12\]
Grundfläche der Pyramide berechnen:
Die Längen der Katheten \([CA]\) und \([CB]\) des rechtwinkligen Dreiecks \(ABC\) sind aus den Teilaufgaben a, b bekannt:
\[\overline{CA} = 9\,; \quad \overline{CB} = 12\]
\[A_{ABC} = \frac{1}{2} \cdot \overline{CA} \cdot \overline{CB} = \frac{1}{2} \cdot 9 \cdot 12 = 54\]
Volumen \(V\) der Pyramide \(ABCS\) berechnen:
\[V = \frac{1}{3} \cdot A_{ABC} \cdot h = \frac{1}{3} \cdot 54 \cdot 12 = 216\]
![Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 1](https://www.mathelike.de//media/mod_zentools/cache/images/e3d995a152e18bb86fa197fdc98b26b8_XL-27be8eb7332c8c848723fe5b75393ea6.jpg "Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 1")
![Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 1](/media/k2/items/cache/e3d995a152e18bb86fa197fdc98b26b8_XL.jpg "Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 1")
![Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 2](https://www.mathelike.de//media/mod_zentools/cache/images/e3017719190ff1e83db12ee09e7beada_XL-de422bb8955f1ed15009a68005503871.jpg "Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 2")
![Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 2](/media/k2/items/cache/e3017719190ff1e83db12ee09e7beada_XL.jpg "Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 2")
![Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 1](https://www.mathelike.de//media/mod_zentools/cache/images/e3d995a152e18bb86fa197fdc98b26b8_XL-27be8eb7332c8c848723fe5b75393ea6-552b3e026a4ca07091a9ad120f827b54.jpg "Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 1")
![Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 2](https://www.mathelike.de//media/mod_zentools/cache/images/e3017719190ff1e83db12ee09e7beada_XL-de422bb8955f1ed15009a68005503871-de6ea2c1e0045be9ef375038488b40bd.jpg "Neigungswinkel der Seitenkante [BS] gegen die Ebene E - Grafik 2")
