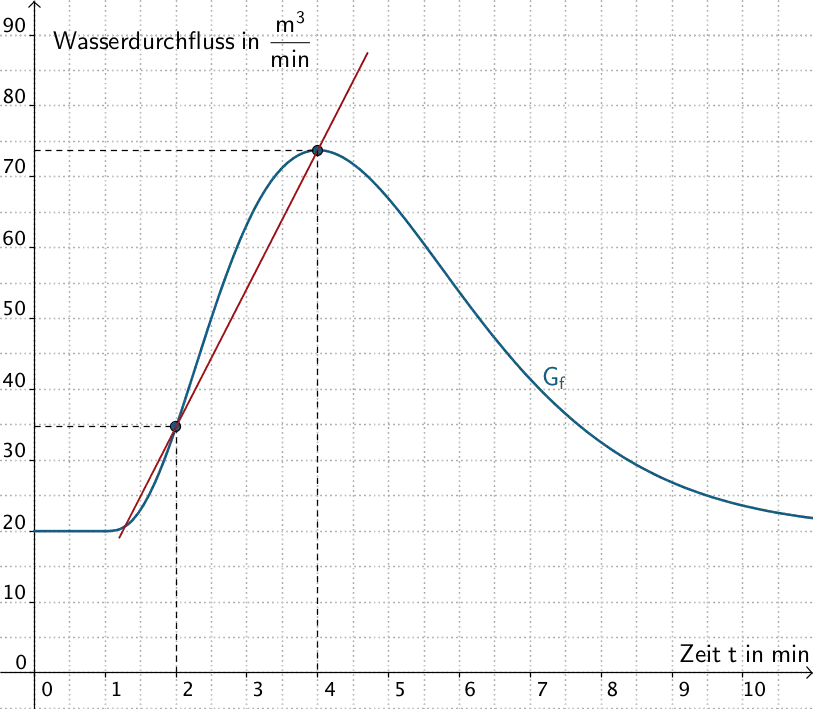
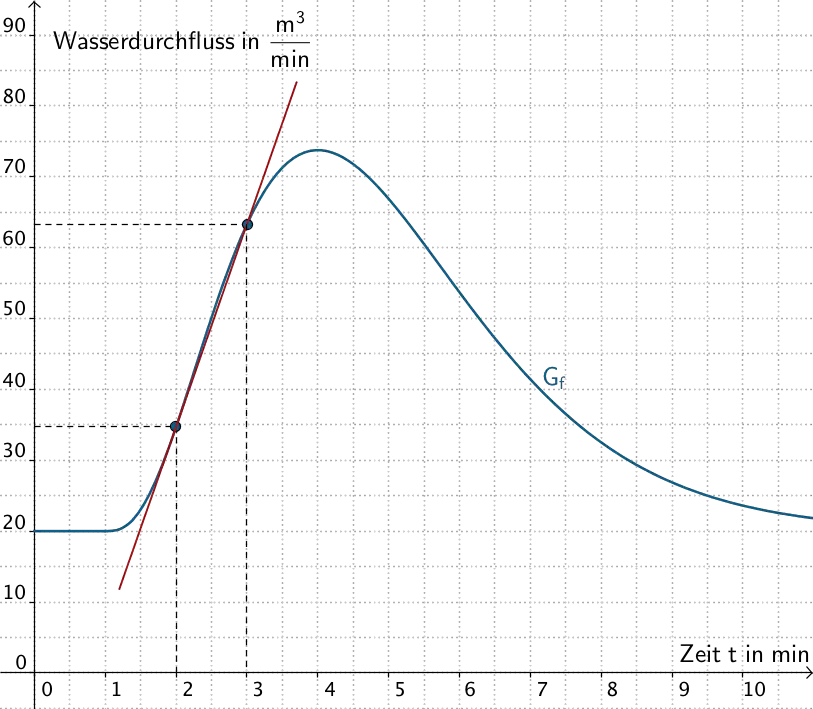
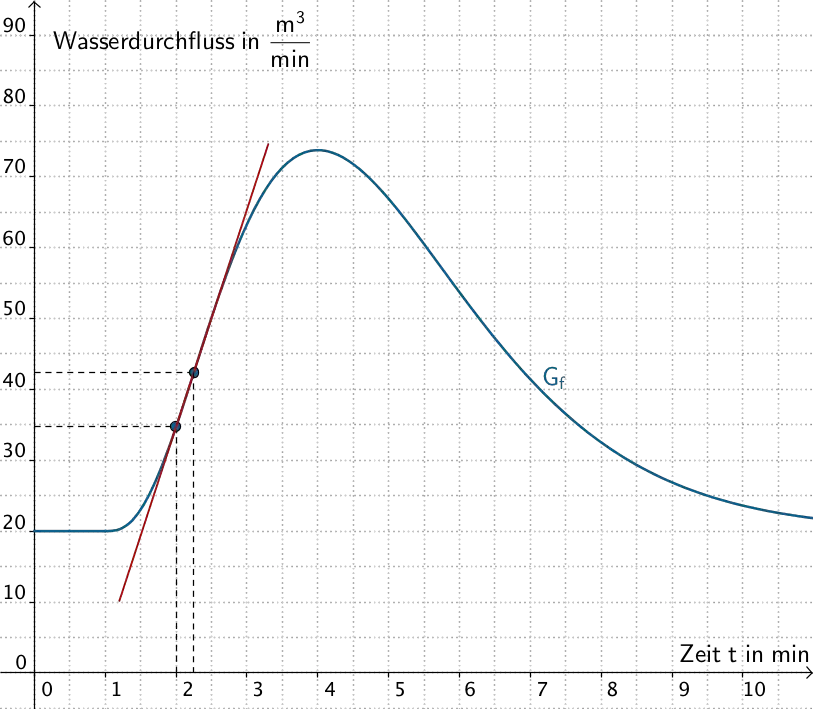
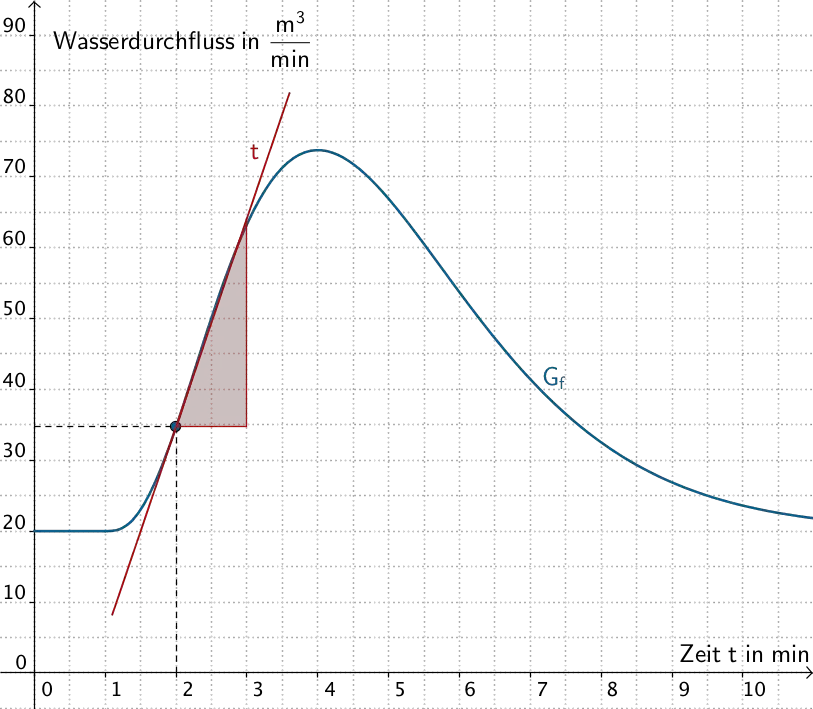
Bestimmen Sie mithilfe von \(G_f\) für \(t = 4\) und \(t = 3\) jeweils einen Näherungswert für die mittlere Änderungsrate von \(f\) im Zeitintervall \([2;t]\,\). Veranschaulichen Sie Ihr Vorgehen in Abbildung 3 durch geeignete Steigungsdreiecke. Welche Bedeutung hat der Grenzwert der mittleren Änderungsraten für \(t \to 2\) im Sachzusammenhang?
(5 BE)
Lösung zu Teilaufgabe 2c
Mittlere Änderungsraten von \(f\) im Zeitintervall \([2;t]\)
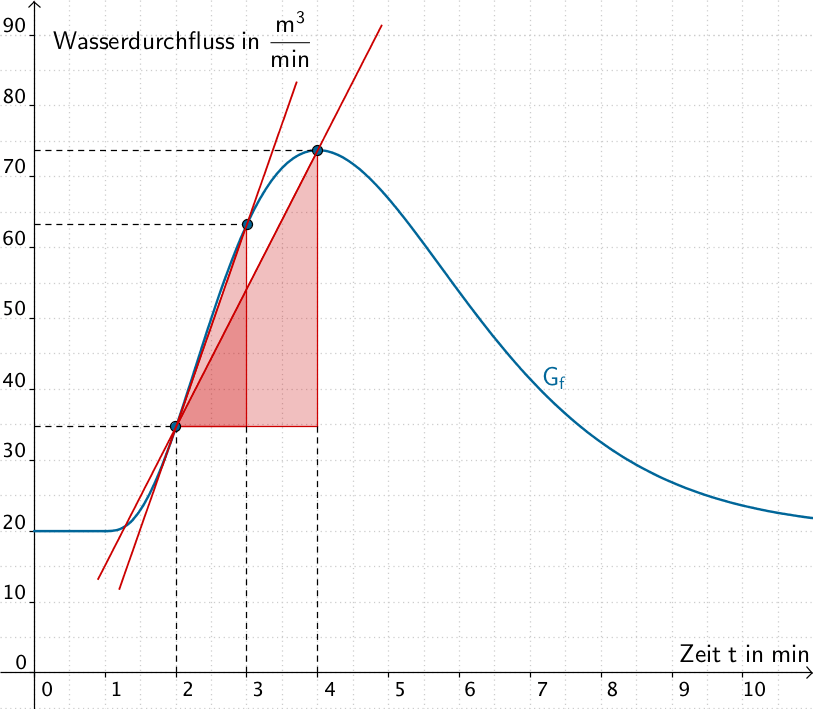
Die mittlere Änderungsrate der Funktion \(\,f\,\) im Intervall \(\,[\,2;t\,]\,\) enspricht der Steigung der Sekante durch die Punkte \(\,(2\,|\,f(2))\,\) und \(\,(t\,|\,f(t))\,\).
Differenzenquotient oder mittlere Änderungsrate
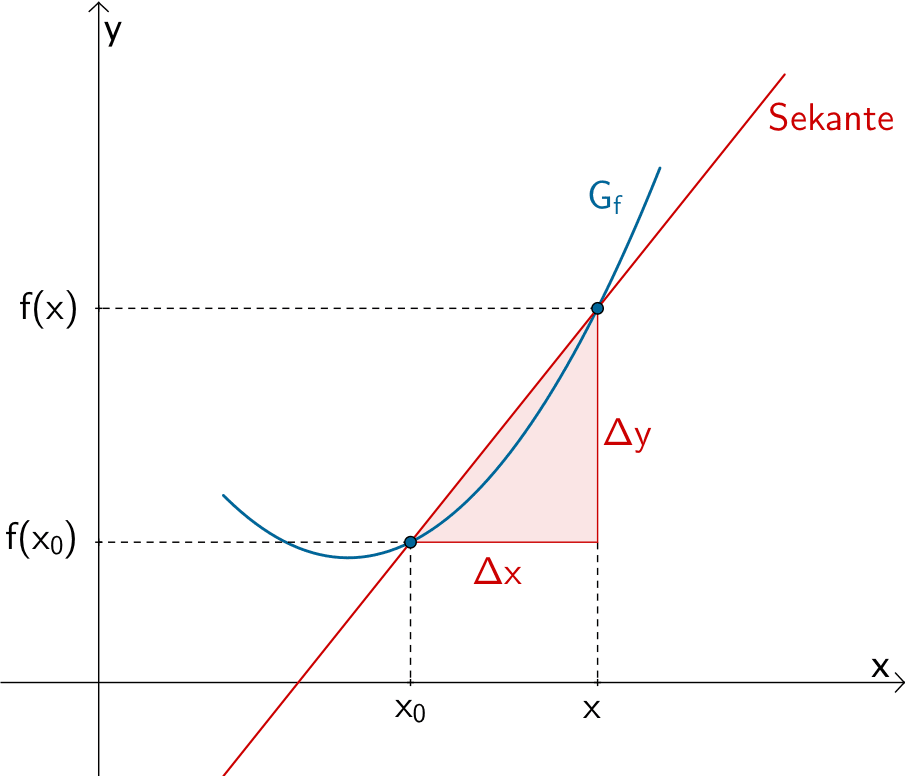
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[m = \frac{f(t) - f(2)}{t - 2}\]
Mittlere Änderungsrate von \(f\) im Zeitintervall \([2;3]\,\):
\[f(2) \approx 35\,\pm\,1\]
\[f(3) \approx 63\,\pm\,1\]
\[\Longrightarrow \quad m = \frac{f(3) - f(2)}{3 - 2} \approx \frac{63 - 35}{3 - 2} = 28\]
Mittlere Änderungsrate von \(f\) im Zeitintervall \([2;4]\,\):
\[f(2) \approx 35\,\pm\,1\]
\[f(4) \approx 74\,\pm\,1\]
\[\Longrightarrow \quad m = \frac{f(4) - f(2)}{4 - 2} \approx \frac{74 - 35}{4 - 2} = 19{,}5\]
Grenzwert der mittleren Änderungsraten für \(t \to 2\) im Sachzusammenhang
Differentialquotient oder lokale bzw. momentane Änderungsrate
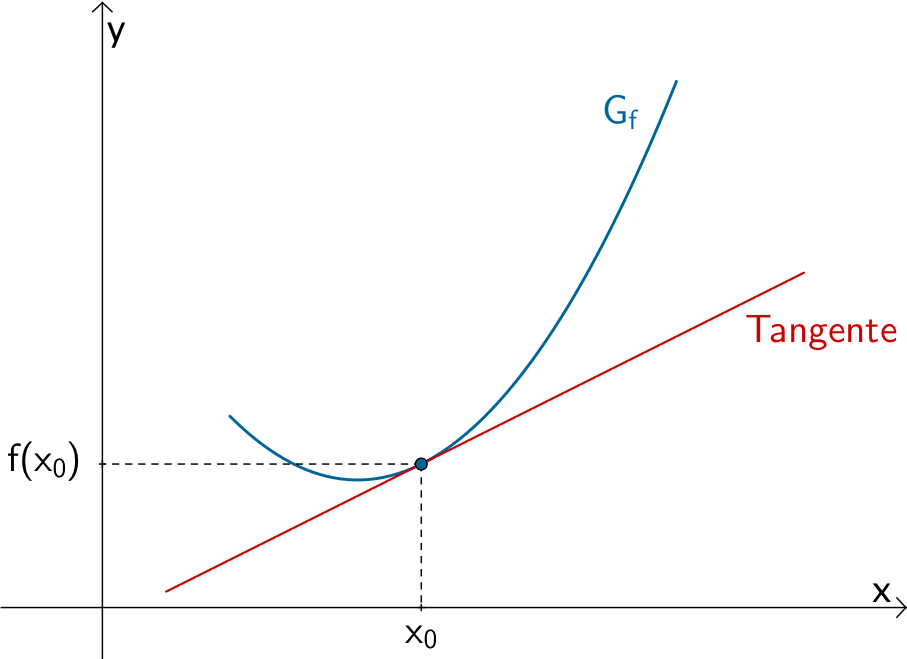
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Der Grenzwert \(\,\displaystyle \lim \limits_{t\,\to\,2} \frac{f(t) - f(2)}{t - 2} = f'(2)\,\) der mittleren Änderungsraten für \(t \to 2\) beschreibt die momentane Änderungsrate des Wasserdurchflusses zum Zeitpunkt \(t = 2\,\). Die Steigung der Tangente an den Graphen von \(f\) an der Stelle \(t = 2\) entspricht dem Wert der momentanen Änderungsrate (Einheit: \(\,\frac{\sf{m}^3}{\sf{min}^2}\)).
\(t = \{4;3;2{,}25\}\): Die Steigung der Sekante beschreibt die mittlere Änderungsrate von \(f\) im Zeitintervall \([2;4]\), \([2;3]\) bzw. \([2;2{,}25]\).
\(t = 2\): Die Steigung der Tangente \(\boldsymbol{t}\) beschreibt die momentane Änderungsrate von \(f\) zum Zeitpunkt \(t = 2\).