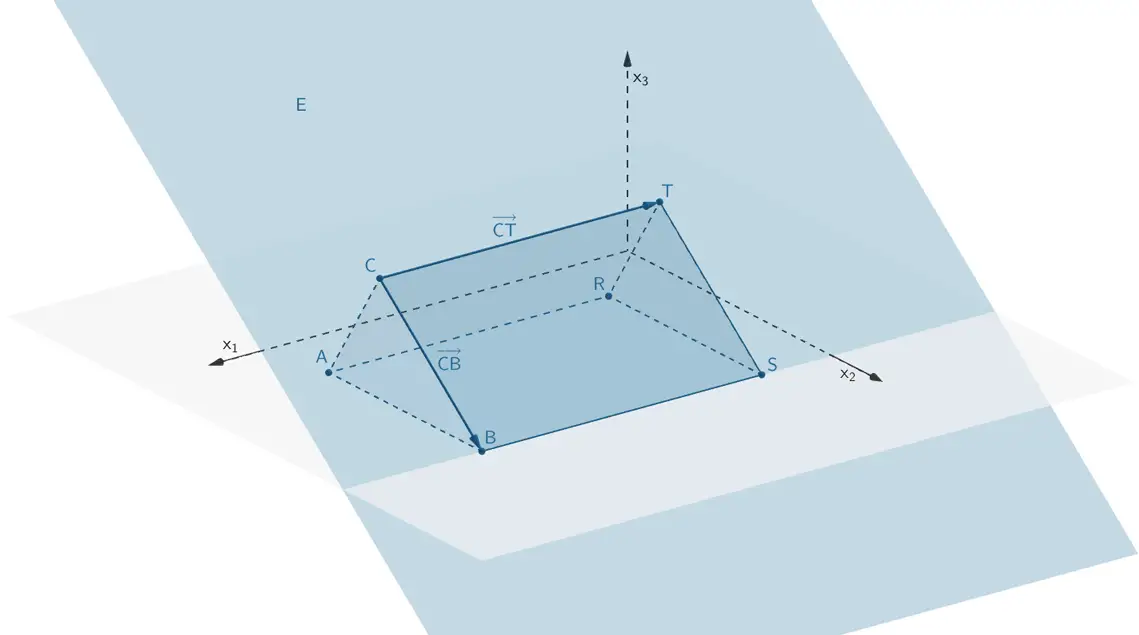
Ermitteln Sie eine Gleichung der Ebene \(E\), in der die Seitenfläche \(BSTC\) liegt, in Normalenform.
(mögliches Ergebnis: \(E \colon 3x_2 + 4x_3 - 24 = 0\))
(4 BE)
Lösung zu Teilaufgabe b
\[BSTC \subset E\]
\[B\,(10|8|0)\,, \enspace S\,(2|8|0)\,, \enspace T\,(2|4|3)\,, \enspace C\,(10|4|3)\]
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
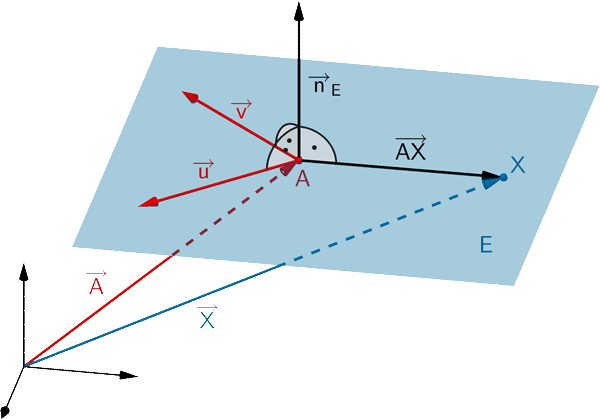
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Richtungsvektoren der Ebene \(E\) bestimmen:
Z.B. sind \(\overrightarrow{CT}\) und \(\overrightarrow{CB}\) zwei linear unabhängige Richtungsvektoren der Ebene \(E\,\).
\[\overrightarrow{CT} = \overrightarrow{T} - \overrightarrow{C} = \begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix} - \begin{pmatrix} 10 \\ 4 \\ 3 \end{pmatrix} = \begin{pmatrix} -8 \\ 0 \\ 0 \end{pmatrix}\]
\[\overrightarrow{CB} = \overrightarrow{B} - \overrightarrow{C} = \begin{pmatrix} 10 \\ 8 \\ 0 \end{pmatrix} - \begin{pmatrix} 10 \\ 4 \\ 3 \end{pmatrix} = \begin{pmatrix} 0 \\ 4 \\ -3 \end{pmatrix}\]
Normalenvektor \(\overrightarrow{n}_E\) der Ebene \(E\) bestimmen:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\begin{align*} \overrightarrow{CT} \times \overrightarrow{CB} &= \begin{pmatrix} -8 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\ 4 \\ -3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 & \cdot & (-3) & - & 0 & \cdot & 4 \\ 0 & \cdot & 0 & - & (-8) & \cdot & (-3) \\ (-8) & \cdot & 4 & - & 0 & \cdot & 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ -24 \\ -32 \end{pmatrix} = -8 \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\end{align*}
\[\Longrightarrow \quad \overrightarrow{n}_E = \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\]
Ebenengleichung in Normalenform in Vektordarstellung aufstellen:
Es sei \(C\,(10|4|3)\) der Aufpunkt der Ebene \(E\,\).
\[\begin {align*} \Longrightarrow \quad &E \colon \enspace \overrightarrow{n}_E \circ \left( \overrightarrow X - \overrightarrow C \right) = 0 \\[0.8em] &E \colon \enspace \begin {pmatrix} 0 \\ 3 \\ 4 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 10 \\ 4 \\ 3 \end {pmatrix} \right] = 0 \end {align*}\]
Ebenengleichung in Normalenform in Koordinatendarstellung bestimmen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin {align*} \begin {pmatrix} 0 \\ 3 \\ 4 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 10 \\ 4 \\ 3 \end {pmatrix} \right] &= 0 \\[0.8em] 0 \cdot (x_1 - 10) + 3 \cdot (x_2 - 4) + 4 \cdot (x_3 - 3) &= 0 \\[0.8em] 3x_2 - 12 + 4x_3 - 12 &= 0 \\[0.8em] 3x_2 + 4x_3 - 24 &= 0 \end {align*}\]
\[E\,\colon \enspace 3x_2 + 4x_3 - 24 = 0\]
Die Seitenfläche \(\,BSTC\,\) des Prismas repräsentiert die Ebene \(E\,\).