Die Abbildung zeigt den Graphen einer Funktion \(f\).
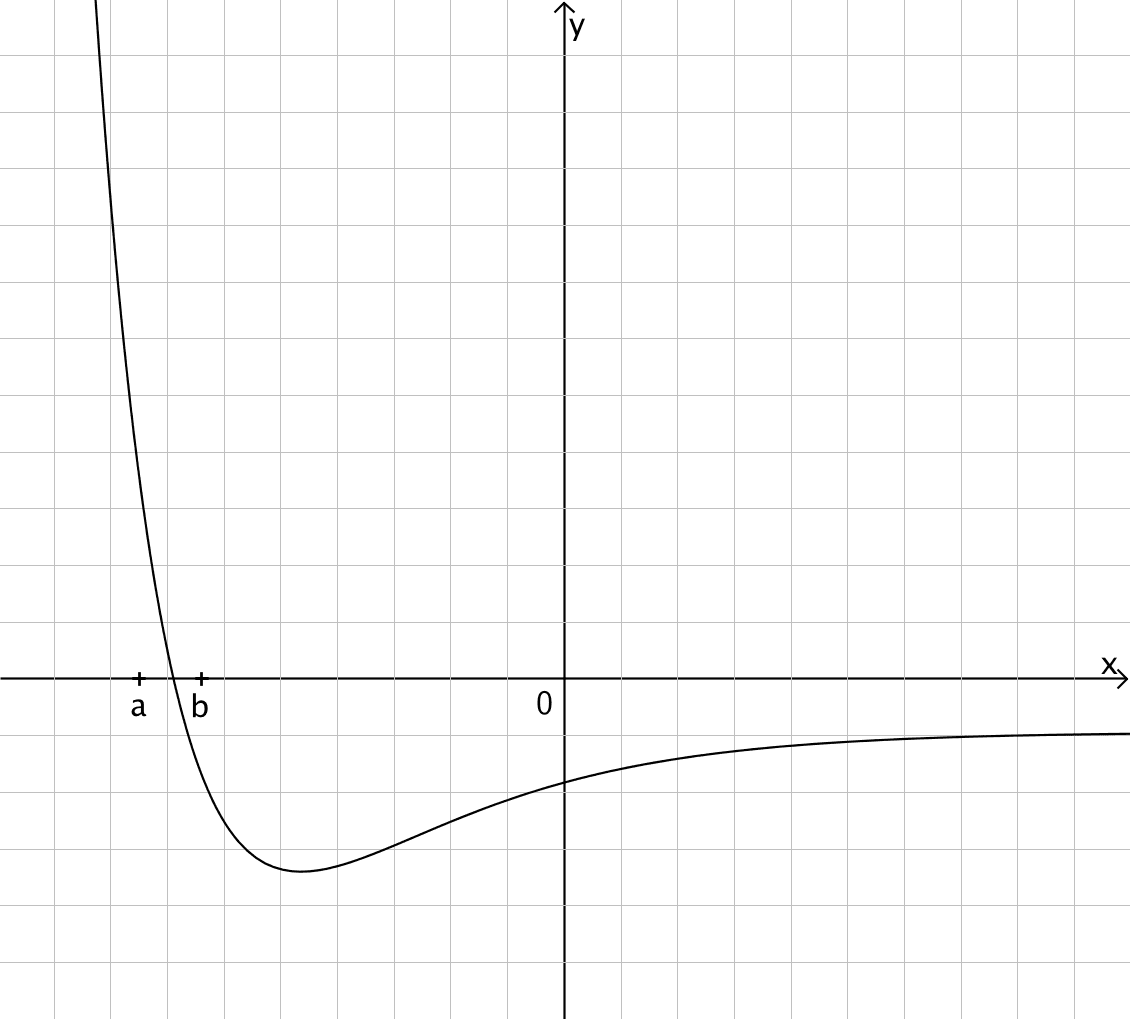
Beschreiben Sie für \(a \leq x \leq b\) den Verlauf des Graphen einer Stammfunktion von \(f\).
(2 BE)
Lösung zu Teilaufgabe 4a
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F'(x) = f(x)\]
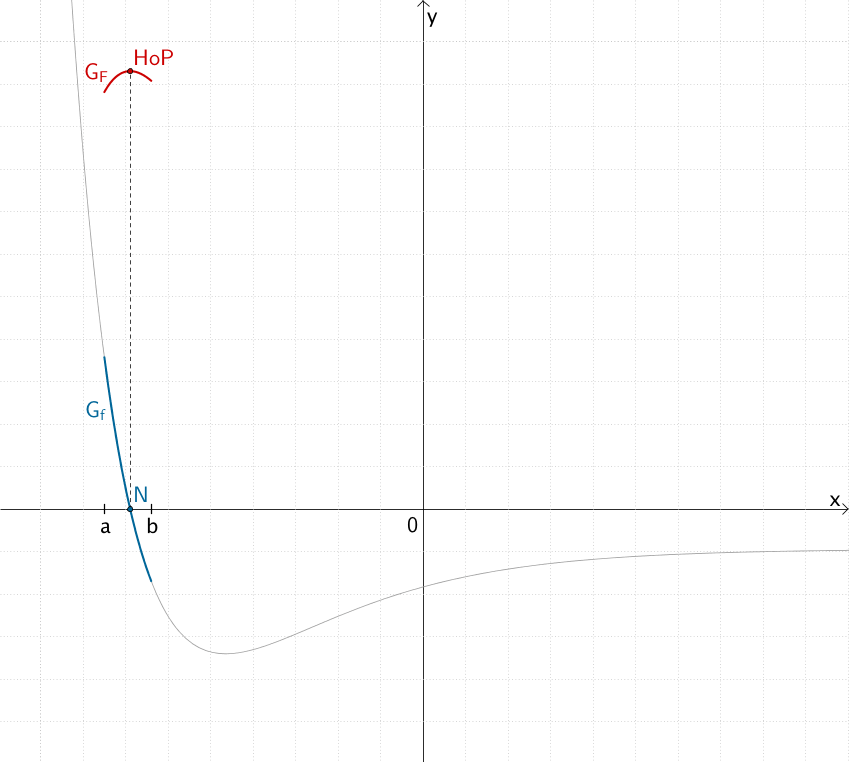
\(G_f\) hat im Intervall \([a;b]\) eine einfache Nullstelle \(x_N\) mit Vorzeichenwechsel von \(+\) nach \(-\). Somit ändert der Graph einer Stammfunktion \(F\) im Intervall \([a;b]\) das Monotonieverhalten von „streng monoton steigend" zu „streng monoton fallend" und besitzt an der Stelle \(x_N\) einen Hochpunkt \(HoP\,(x_N|F(x_N))\).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*} &F'(x) > 0 \enspace \text{für} \enspace x < x_{N} \\ &F'(x_{N}) = 0 \\ &F'(x) < 0 \enspace \text{für} \enspace x > x_{N} \end{align*} \right \} \enspace \Rightarrow \enspace \text{Hochpunkt} \; HoP\,(x_{N}|F(x_{N}))\]
Anmerkung: Die Abbildung zeigt im Intervall \([a;b]\) den Graphen \(G_F\) der Stammfunktion \(\displaystyle F(x) = \int_0^x f(x)\,dx\). Die Menge aller Stammfunktionen von \(f\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int f(x)\,dx\). Die Stammfunktionen unterscheiden sich im Wert einer additiven Integrationskonstante \(C\), welche den Graphen einer Stammfunktion von \(f\) in \(y\)-Richtung verschiebt. Der Hochpunkt an der Stelle \(x_N\) kann somit in \(y\)-Richtung beliebig skizziert werden. Der charakteristische Verlauf des Graphen einer Stammfunktion von \(f\) bleibt derselbe (siehe Teilaufgabe 4b).

