Normalenvektor

Ein auf einer Stange montierter Brunnen besteht aus einer Marmorkugel, die in einer Bronzeschale liegt. Die Marmorkugel berührt die vier Innenwände der Bronzeschale an jeweils genau einer Stelle. Die Bronzeschale wird im Modell durch die Seitenflächen der Pyramide \(ABCDS\) beschrieben, die Marmorkugel durch eine Kugel mit Mittelpunkt \(M(0|0|4)\) und Radius \(r\). Die \(x_{1}x_{2}\)-Ebene des Koordinatensystems stellt im Modell den horizontal verlaufenden Erdboden dar; eine Längeneinheit entspricht einem Dezimeter in der Realität.

Ermitteln Sie den Durchmesser der Marmorkugel auf Zentimeter genau.

(zur Kontrolle: \(r = \sqrt{6}\))

(4 BE)

Das Dreieck \(ABF\) liegt in der Ebene \(W\). Ermitteln Sie eine Gleichung von \(W\) in Koordinatenform und beschreiben Sie die besondere Lage von \(W\) im Koordinatensystem.

(zur Kontrolle: \(W \colon 4x_{2} + 3x_{3} - 20 = 0\))

(4 BE)

Berechnen Sie die Größe des spitzen Winkels, den die Seitenfläche \(ABF\) und die Grundfläche \(ABCD\) einschließen.

(3 BE)

Untersuchen Sie, ob \(K\) die \(x_1x_2\)-Ebene schneidet.

(2 BE)

Bestimmen Sie eine Gleichung der Ebene \(E\) in Koordinatenform und zeigen Sie, dass die Gerade \(g\) in \(E\) liegt.

(zur Kontrolle: \(E \colon 2x_1 - x_2 + 2x_3 + 35 = 0\))

(5 BE)

Bestimmen Sie die Größe des Winkels, unter dem der Meeresboden gegenüber der Wasseroberfläche abfällt.

(3 BE)

Die Ebene \(E\) enthält die Punkte \(A\), \(B\) und \(C\), die Ebene \(F\) die Punkte \(B\), \(C\) und \(D\).

Bestimmen Sie eine Gleichung von \(E\) in Koordinatenform.

(zur Kontrolle: \(14x_1 + 14x_2 + 11x_3 = 308\))

(4 BE)

Berechnen Sie die Größe \(\varphi\) des Winkels, unter dem \(E\) die \(x_1x_2\)-Ebene schneidet. Geben Sie einen Term an, mit dem aus \(\varphi\) die Größe des Winkels zwischen den Ebenen \(E\) und \(F\) berechnet werden kann.

(5 BE)

Gegeben ist die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\) mit \(\lambda \in \mathbb R\).

Zeigen Sie, dass \(g\) in der Ebene mit der Gleichung \(x_1 + x_2 + x_3 = 2\) liegt.

(2 BE) 

Bestimmen Sie eine Gleichung von \(L\) in Koordinatenform sowie die Größe \(\varphi\) des Winkels, den \(L\) mit der \(x_1x_2\)-Ebene einschließt.

(zur Kontrolle: \(x_1+x_2+x_3-19= 0; \enspace \varphi \approx 55^{\circ}\))

(6 BE) 

Die Abbildung zeigt den Körper \(ABCDEF\) mit \(A(6|3|0)\), \(B(0|6|0)\), \(C(3|0|0)\), \(D(6|3|6)\), \(E(0|6|6)\) und \(F(3|0|12)\).
Die Punkte \(D\), \(E\) und \(F\) liegen in der Ebene \(L\).

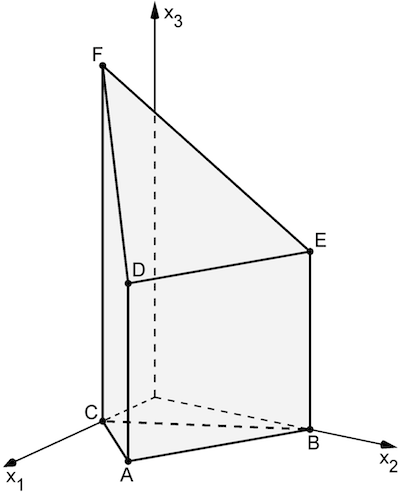
Ermitteln Sie eine Gleichung von \(L\) in Koordinatenform.

(zur Kontrolle: \(2x_1 + 4x_2 + 3x_3 - 42 = 0\))

(4 BE) 

Bestimmen Sie die Größe des Winkels, den \(L\) mit der \(x_1x_2\)-Ebene einschließt.

(3 BE) 

Die Ebene \(N_k\) enthält die \(x_3\)-Achse und den Punkt \(P_k(1-k|k|0)\) mit \(k \in \; ]0;1[\). Welche Kanten des Körpers von \(N_k\) geschnitten werden, ist abhängig von \(k\). Durchläuft \(k\) alle Werte zwischen \(0\) und \(1\), so gibt es Bereiche \(]a;b[\), für die jeweils gilt, dass \(N_k\) für alle Werte von \(k \in \; ]a;b[\) die gleichen Kanten des Körpers schneidet. Bestimmen Sie den größten dieser Bereiche und geben Sie die zugehörigen Kanten an.

(4 BE) 

Der Umkreis des Dreiecks \(ABC\) und der Punkt \(S\) legen einen Kegel fest. Zeigen Sie, dass es sich um einen geraden Kegel handelt, der Mittelpunkt des Grundkreises also zugleich der Höhenfußpunkt des Kegels ist. Berechnen Sie, um wie viel Prozent das Volumen des Kegels größer ist als das Volumen der Pyramide \(ABCS\).

(7 BE)

Überprüfen Sie rechnerisch, ob das Fenster bei seiner Drehung am Möbelstück anstoßen kann.

(5 BE)

Das Dreieck \(ABC\) aus Aufgabe \(a\) ist die Grundfläche einer dreiseitigen Pyramide \(ABCS\) mit der Spitze \(S(11{,}5|4|-6)\).

Die Grundfläche der Pyramide liegt in einer Ebene \(E\). Ermitteln Sie eine Gleichung von \(E\) in Normalenform.

(mögliches Ergebnis: \(E\colon \enspace 2x_1 + x_2 -2x_3 - 3 = 0)\)

(3 BE)

Berechnen Sie die Größe des Neigungswinkels der Seitenkante \([BS]\) gegen die Ebene \(E\) sowie das Volumen \(V\) der Pyramide.

(Teilergebnis: \(V = 216\))

(7 BE)

Zeigen Sie, dass dieser Abstand mit der minimalen Entfernung des Hubschraubers vom Mittelpunkt des Grundstücks übereinstimmt, der im Modell durch den Punkt \(M(-40|30|30)\) dargestellt wird.

(5 BE)

Ermitteln Sie eine Gleichung der Ebene \(E\), in der die Seitenfläche \(BSTC\) liegt, in Normalenform.

(mögliches Ergebnis: \(E \colon 3x_2 + 4x_3 - 24 = 0\))

(4 BE)

Abbildung 1 zeigt modellhaft ein Dachzimmer in der Form eines geraden Prismas. Der Boden und zwei Seitenwände liegen in den Koordinatenebenen. Das Rechteck \(ABCD\) liegt in einer Ebene \(E\) und stellt den geneigten Teil der Deckenfläche dar.

Abb. 1

Bestimmen Sie eine Gleichung der Ebene \(E\) in Normalenform.

(mögliches Ergebnis: \(E \colon x_2 + 2x_3 - 8 = 0\))

(4 BE)