Die Tangente an den Graphen der Funktion \(f\) mit \(f(x) = 0{,}5x^2\) im Punkt \(P(2|f(2))\) und die Normale bilden mit der \(x\)-Achse das Dreieck \(PQR\).
a) Veranschaulichen Sie den Sachverhalt in einer Skizze.
b) Berechnen Sie den Flächeninhalt sowie die Innenwinkel des Dreiecks.
a) Skizze des Sachverhalts
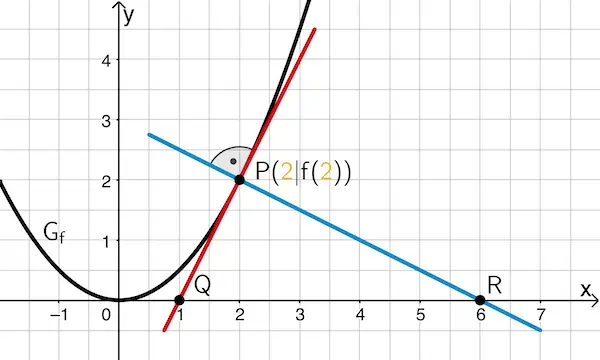
Die Tangente und die Normale im Punkt \(P(\textcolor{#e9b509}{2}|f(\textcolor{#e9b509}{2}))\) des Graphen der Funktion \(f \colon x \mapsto 0{,}5x^2\) bilden mit der \(x\)-Achse das Dreieck \(PQR\).
b) Flächeninhalt und Innenwinkel des Dreiecks \(PQR\)
Berechnung des Flächeninhalts des Dreiecks \(\boldsymbol{PQR}\)
Vorgehensweise
- Gleichung der Tangente und Gleichung der Normale ermitteln.
- Jeweils Nullstelle der Tangente und der Normale bestimmen.
- Flächeninhalt des Dreiecks \(PQR\) berechnen.
Gleichung der Tangente
Ansatz: \(y = \textcolor{#cc071e}{m}x + t\)
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
1. Schritt: Steigung \(\textcolor{#cc071e}{m_t}\) der Tangente berechnen
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\(\textcolor{#cc071e}{m_t} = f'(\textcolor{#e9b509}{2})\)
Erste Ableitung \(f'\) bilden:
Benötigte Ableitungen/Ableitungsregel: Faktorregel, Potenzregel (Ableitung einer Potenzfunktion)
\[f(x) = 0{,}5x^2\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[f'(x) = 0{,}5 \cdot 2 \cdot x = x\]
\(\textcolor{#cc071e}{m_t} = f'(\textcolor{#e9b509}{2}) = \textcolor{#cc071e}{2}\)
2. Schritt: \(y\)-Achsenabschnitt \(t\) berechnen
Hierfür wird der Wert der Steigung \(\textcolor{#cc071e}{m_t}\) der Tangente sowie die Koordinaten des Punktes \(P(\textcolor{#e9b509}{2}|f(\textcolor{#e9b509}{2}))\) in die Geradengleichung eingesetzt und diese nach \(t\) aufgelöst. Zunächst ist noch die \(y\)-Koordinate von \(P\) zu berechnen.
\[f(\textcolor{#e9b509}{2}) = 0{,}5 \cdot \textcolor{#e9b509}{2}^2 = \textcolor{#89ba17}{2} \; \Rightarrow \; P(\textcolor{#e9b509}{2}|\textcolor{#89ba17}{2})\]
\[\begin{align*}\textcolor{#89ba17}{2} &= \textcolor{#cc071e}{2} \cdot \textcolor{#e9b509}{2} + t \\[0.8em] 2 &= 4 + t &&| -4 \\[0.8em] -2 &= t\end{align*}\]
Gleichung der Tangente: \(y = 2x - 2\)
Gleichung der Normale
Ansatz: \(y = \textcolor{#0087c1}{m}x + t\)
1. Schritt: Steigung \(\textcolor{#0087c1}{m_n}\) der Normale berechnen
Für die Steigungen \(m_1\) und \(m_2\) zweier zueinander senkrechter Geraden \(g_1\) und \(g_2\) gilt: \(m_1 \cdot m_2 = -1\).
Zueinander parallele / senkrechte (orthogonale) Geraden
\[g_1 \colon y = m_1\cdot x + t_1; \enspace g_2 \colon y = m_2\cdot x + t_2\]
parallele Geraden:
\[m_1 = m_2 \; \Leftrightarrow \; g_1 \parallel g_2\]
senkrechte (orthogonale) Geraden:
\[m_1 \cdot m_2 = -1 \; \Leftrightarrow \; g_1 \perp g_2\]
Analog gilt für die Steigungen einer Tangente und einer Normale:
Anwendung der Differetialrechnung:
Tangentensteigung und Normalensteigung
Tangentensteigung: \(m_{T} = f'(x_0)\)
Normalensteigung: \(m_{N} = -\dfrac{1}{f'(x_0)}\)
(vgl. Merkhilfe)
\[\textcolor{#cc071e}{m_t} \cdot \textcolor{#0087c1}{m_n} = -1\; \Leftrightarrow \; \textcolor{#0087c1}{m_n} = -\frac{1}{\textcolor{#cc071e}{m_t}}\]
\[\textcolor{#0087c1}{m_n} = -\frac{1}{\textcolor{#cc071e}{m_t}} = -\frac{1}{\textcolor{#cc071e}{2}} = \textcolor{#0087c1}{-\frac{1}{2}}\]
2. Schritt: \(y\)-Achsenabschnitt \(t\) berechnen
\(\textcolor{#0087c1}{m_n} = \textcolor{#0087c1}{-\dfrac{1}{2}}\); \(P(\textcolor{#e9b509}{2}|\textcolor{#89ba17}{2})\)
\[\begin{align*} \textcolor{#89ba17}{2} &= \textcolor{#0087c1}{-\frac{1}{2}} \cdot \textcolor{#e9b509}{2} + t \\[0.8em] 2 &= -1 + t &&| + 1 \\[0.8em] 3 &= t \end{align*}\]
Gleichung der Normale: \(y = -\dfrac{1}{2}x + 3\)
Nullstelle der Tangente
\[\begin{align*}2x - 2 &= 0 &&| + 2 \\[0.8em] 2x &= 2 &&| : 2 \\[0.8em] x &= 1\end{align*}\]
\[\Rightarrow\; Q(\textcolor{#e9b509}{1}|0)\]
Nullstelle der Normale
\[\begin{align*}-\frac{1}{2}x + 3 &= 0 &&| - 3 \\[0.8em] -\frac{1}{2}x &= -3 &&| \cdot (-2) \\[0.8em] x &= 6\end{align*}\]
\[\Rightarrow\; R(\textcolor{#e9b509}{6}|0)\]
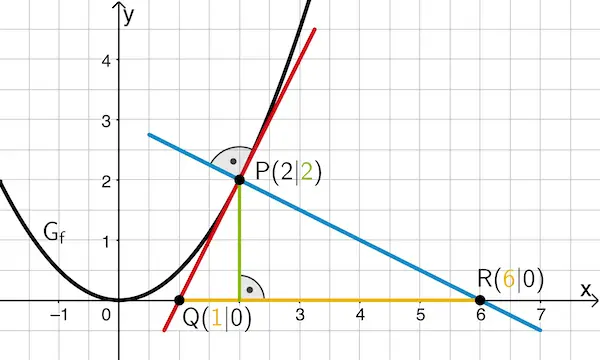
Flächeninhalt des Dreiecks \(\boldsymbol{PQR}\) berechnen
 (Ergänzungen optional)
(Ergänzungen optional)
\[A_{PQR} = \frac{1}{2} \cdot \textcolor{#e9b509}{g} \cdot \textcolor{#89ba17}{h} = \frac{1}{2} \cdot \textcolor{#e9b509}{(6 - 1)} \cdot \textcolor{#89ba17}{2} = 5\]
Der Flächeninhalt des Dreiecks \(PQR\) beträgt 5 FE (Flächeneinheiten).
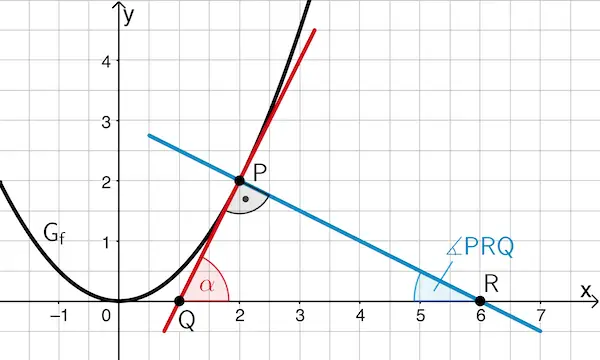
Innenwinkel des Dreiecks \(\boldsymbol{PQR}\)
 (Ergänzungen optional)
(Ergänzungen optional)
Da das Dreieck \(PQR\) bei \(P\) rechtwinklig ist, genügt es, einen Innenwinkel zu berechnen. Der Steigungswinkel \(\textcolor{#cc071e}{\alpha}\) der Tangente entspricht dem Innenwinkel des Dreiecks bei \(Q\), das heißt, dem Winkel \(\textcolor{#cc071e}{\measuredangle{RQP}}\).
MIt der Tangentensteigung \(\textcolor{#cc071e}{m_t = 2}\) (vgl. oben) ergibt sich:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\begin{align*}\tan{\textcolor{#cc071e}{\alpha}} &= \textcolor{#cc071e}{m_t} \\[0.8em]\tan{\textcolor{#cc071e}{\alpha}} &= \textcolor{#cc071e}{2} &&| \; \text{Taschenrechner:}\; \tan^{-1}{(\textcolor{#cc071e}{2})} \\[1.6em] \textcolor{#cc071e}{\alpha} &\approx \textcolor{#cc071e}{63{,}4^{\circ}} \end{align*}\]
\[\Rightarrow \; \textcolor{#cc071e}{\measuredangle{RQP}} \approx \textcolor{#cc071e}{63{,}4^{\circ}}\]
\[\Rightarrow \; \textcolor{#0087c1}{\measuredangle{PRQ}} \approx 90^{\circ} - \textcolor{#cc071e}{63{,}4^{\circ}} = \textcolor{#0087c1}{26{,}6^{\circ}}\]

