Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{4x + 4}{x^{2}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Geben Sie die maximale Definitionsmenge sowie die Nullstelle(n) und die Polstelle(n) der Funktion \(f\) an. Bestimmen Sie die Gleichungen aller Asymptoten des Graphen der Funktion \(f\).
b) Untersuchen Sie das Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems.
c) Leiten Sie die Funktion \(f\) sowohl mit der Produkt- als auch der Quotientenregel ab.
(Zur Kontrolle: \(f'(x) = \dfrac{-4x - 8}{x^{3}}\))
d) Bestimmen Sie die Nullstelle(n) der Ableitungsfunktion und deuten Sie das Ergebnis geometrisch.
e) Ermitteln Sie die Gleichung der Tangente \(T\) an \(G_{f}\) an der Stelle \(x = 2\).
a) Maximale Definitionsmenge, Nullstelle(n) und Polstelle(n) von \(f\) sowie Gleichungen aller Asymptoten von \(G_{f}\)
\[f(x) = \frac{4x + 4}{x^{2}}\]
Maximale Definitionsmenge von \(f\)
Da die Division durch Null in der Mathematik nicht erlaubt ist, ist die gebrochenrationale Funktion \(f\) an den Nullstellen des Nennerterms nicht definiert.
\[\Longrightarrow \quad D_{f} = \mathbb R \backslash \{0\}\]
Nullstelle(n) von \(f\)
\[f(x) = \frac{4x + 4}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
Ein Bruchterm ist gleich Null, wenn der Zählerterm gleich Null ist.
\[\begin{align*}f(x) = 0 \quad \Longrightarrow \quad 4x + 4 &= 0 & &| - 4 \\[0.8em] 4x &= -4 & &| : 4 \\[0.8em] x &= -1 \end{align*}\]
oder
\[\begin{align*}f(x) = 0 \quad \Longrightarrow \quad 4x + 4 &= 0 \\[0.8em] 4 \cdot (x + 1) &= 0 \\[0.8em] x &= -1 \end{align*}\]
\(x = -1\) ist einzige Nullstelle der gebrochenrationalen Funktion \(f\).
Polstellen von \(f\)
\[f(x) = \frac{4x + 4}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
Da die Nennernullstelle \(x = 0\) nicht zugleich eine Nullstelle des Zählers ist, ist die Definitionslücke \(x = 0\) nicht hebbar. Folglich ist \(x = 0\) eine Polstelle der gebrochenrationalen Funktion \(f\). Zudem ist \(x = 0\) eine doppelte Nennernullstelle, was auf eine Polstelle ohne Vorzeichenwechsel schließen lässt.
Anmerkung
Eine hebbare Definitionslücke einer gebrochenrationalen Funktion liegt immer dann vor, wenn eine Nennernullstelle zugleich Zählernullstelle ist und der Funktionsterm so gekürzt werden kann, dass keine Nennernullstelle mehr existiert. Der Graph der gebrochenrationalen Funktion zeigt dann an der entsprechenden Stelle ein Definitionsloch, während er in der Umgebung einer Polstelle gegen \(- \infty\) bzw. \(+ \infty\) strebt.
Gleichungen aller Asymptoten von \(G_{f}\)
Senkrechte Asymptote(n):
An einer Polstelle besitzt der Graph einer gebrochenrationalen Funktion eine senkrechte Asymptote.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\(x = 0\) ist Polstelle der gebrochenrationalen Funktion \(f\).
\(\Longrightarrow \quad\)Senkrechte Asymptote mit der Gleichung \(x = 0\)
Waagrechte oder schräge Asymptote(n):
Der Graph einer gebrochenrationalen Funktion kann für \(x \to +\infty\) bzw. \(x \to -\infty\) eine waagrechte oder schräge Asymptote besitzen.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\[f(x) = \frac{4x + 4}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
Der Grad des Nennerpolynoms von \(f\) ist größer als der Grad des Zählerpolynoms. Folglich ist die \(x\)-Achse mit der Gleichung \(y = 0\) waagrechte Asymptote der gebrochenrationalen Funktion \(f\).
Dies lässt sich durch die Grenzwertbetrachtung \(\lim \limits_{x\,\to\,+\,\infty} f(x)\) bzw. \(\lim \limits_{x\,\to\,-\,\infty} f(x)\) bestätigen.
Für eine aussagekräftige Grenzwertbetrachtung \(\lim \limits_{x \, \to \, \pm \infty} f(x)\) wird die höchste Potenz des Nennerpolynoms im Nenner und im Zähler ausgeklammert.
\[\begin{align*} \lim \limits_{x\,\to\,\pm\,\infty} f(x) &= \lim \limits_{x\,\to\,\pm\,\infty} \frac{4x + 4}{x^{2}} \\[0.8em] &= \lim \limits_{x\,\to\,\pm\,\infty} \frac{\cancel{x^{2}} \cdot \Big( \overbrace{\frac{4}{x}}^{\to\,0} + \overbrace{\frac{4}{x^{2}}}^{\to\,0} \Big)}{\cancel{x^{2}} \cdot 1} & &| \; (x \neq 0) \\[0.8em] &= 0 \end{align*}\]
\(\Longrightarrow \quad\)Waagrechte Asymptote mit der Gleichung \(y = 0\) (\(x\)-Achse)
b) Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems
Man bestimmt den Funktionsterm \(f(-x)\). Gilt \(f(-x) = f(x)\), ist \(G_{f}\) achsensymmetrisch zur \(y\)-Achse. Gilt \(f(-x) = -f(x)\), ist \(G_{f}\) punktsymmetrisch zum Koordinatenursprung \(O(0|0)\). Trifft keiner der beiden Fälle zu, weist \(G_{f}\) keines der beiden Symmetrieverhalten auf.
Symmetrieverhalten von Funktionsgraphen bzgl. des Koordinatensystems
\(f(-x) = f(x) \hspace{32px} \Longrightarrow \quad G_f\) ist achsensymmetrisch zur \(y\)-Achse
\(f(-x) = -f(x) \hspace{20px} \Longrightarrow \quad G_f\) ist punktsymmetrisch zum Ursprung
\[f(x) = \frac{4x + 4}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
\[f(-x) = \frac{4 \cdot (-x) + 4}{(-x)^{2}} = \frac{-4x + 4}{x^{2}}\]
\[\Longrightarrow \quad f(-x) \neq f(x); \; f(-x) \neq -f(x)\]
Der Graph \(G_{f}\) der Funktion \(f\) ist weder achsensymmetrisch zur \(y\)-Achse noch punktsymmetrisch zum Koordinatenursprung.
c) Ableitung der Funktion \(f\) mit der Produkt- als auch der Quotientenregel
\[f(x) = \frac{4x + 4}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
Mithilfe der Rechenregel für Potenzen \(a^{-n} = \frac{1}{a^{n}};\; a \in \mathbb R \backslash \{0\}, \; n \in \mathbb N\) lässt sich der Funktionsterm \(f(x)\) als Produkt formulieren.
\[f(x) = \frac{4x + 4}{x^{2}} = (4x + 4) \cdot x^{-2}\]
Neben der Produktregel bzw. der Quotientenregel wird die Ableitung einer Potenzfunktion sowie die Summen- und die Faktorregel benötigt, um die Funktion \(f\) abzuleiten.
Ableitung der Funktion \(f\) mithilfe der Quotientenregel:
\[f(x) = \frac{4x + 4}{x^{2}}\]
Quotientenregel
\[f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\left[ \frac{u(x)}{v(x)} \right]' = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{\left[ v(x) \right]^{2}}\]
\[u(x) = 4x + 4; \; u'(x) = 4 + 0 = 4\]
\[v(x) = x^{2}; \; v'(x) = 2x\]
\[\begin{align*} f'(x) &= \frac{4 \cdot x^{2} - (4x + 4) \cdot 2x}{\left( x^{2} \right)^{2}} \\[0.8em] &= \frac{4x^{2} - 8x^{2} - 8x}{x^{4}} \\[0.8em] &= \frac{-4x^{2} - 8x}{x^{4}} \\[0.8em] &= \frac{\cancel{x} \cdot (-4x - 8)}{\cancel{x} \cdot x^{3}} \\[0.8em] &= \frac{-4x - 8}{x^{3}} \end{align*}\]
Ableitung der Funktion \(f\) mithilfe der Produktregel:
\[f(x) = (4x + 4) \cdot x^{-2}\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\left[u(x) \cdot v(x)\right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
\[u(x) = 4x + 4; \; u'(x) = 4 + 0 = 4\]
\[v(x) = x^{-2}; \, v'(x) = -2x^{-3}\]
\[\begin{align*} f'(x) &= 4 \cdot x^{-2} + (4x + 4) \cdot (-2x^{-3}) \\[0.8em] &= 4x^{-2} - 8x^{-2} - 8x^{-3} \\[0.8em] &= -4x^{-2} - 8x^{-3} & &| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= -\frac{4}{x^{2}} - \frac{8}{x^{3}} \\[0.8em] &= -\frac{4 \cdot x}{x^{2} \cdot x} - \frac{8}{x^{3}} \\[0.8em] &= \frac{-4x - 8}{x^{3}} \end{align*}\]
d) Nullstelle(n) von \(f'\) und deren geometrische Bedeutung
\[f'(x) = \frac{-4x - 8}{x^{3}}\]
Die Nullstelle(n) der gebrochenrationalen Ableitungsfunktion \(f'\) sind die Nullstelle(n) des Zählers \(-4x - 8\), welche nicht zugleich Nullstellen des Nenners sein dürfen (vgl. Anmerkung).
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
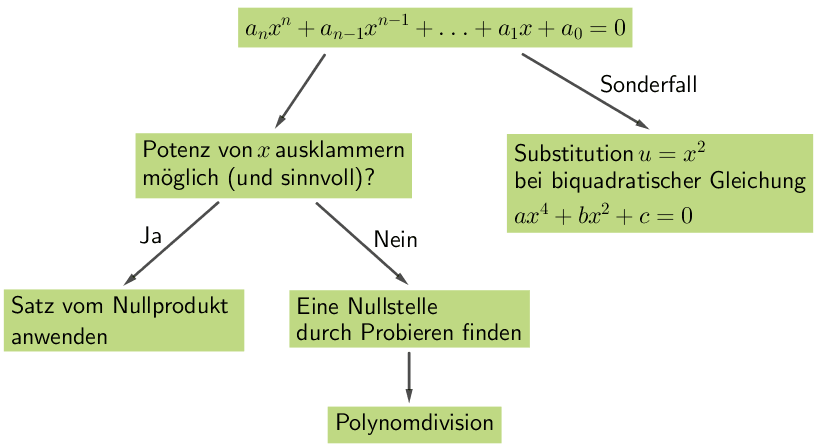
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
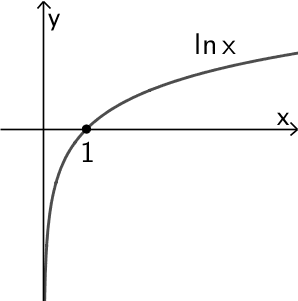
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
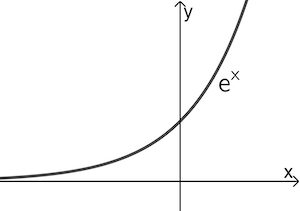
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[\begin{align*} f'(x) = 0 \quad \Longrightarrow \quad -4x - 8 &= 0 & &| + 8 \\[0.8em] -4x &= 8 & &| : (-4) \\[0.8em] x &= -2 \end{align*}\]
oder
\[\begin{align*} f'(x) = 0 \quad \Longrightarrow \quad -4x - 8 &= 0 \\[0.8em] -4 \cdot (x + 2) &= 0 \\[0.8em] x &= -2 \end{align*}\]
Anmerkung:
Ist \(x_0\) eine Nullstelle der Zählerfunktion \(\boldsymbol{z(x)}\) und zugleich eine eine vollständig kürzbare Nullstelle der Nennerfunktion \(\boldsymbol{n(x)}\), so besitzt eine gebrochnrationale Funktion \(f \colon x \mapsto \dfrac{z(x)}{n(x)}\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Geometrische Bedeutung der Nullstelle \(x = -2\) von \(f'\):
Die Ableitungsfunktion \(f'\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\). Das Ergebnis \(f'(-2) = 0\) bedeutet, dass der Graph der Funktion \(f\) an der Stelle \(x = -2\) eine waagrechte Tangente hat. Dies lässt auf einen Extrem- oder Terrassenpunkt von \(G_{f}\) an der Stelle \(x = -2\) schließen.
e) Gleichung der Tangente \(T\) an \(G_{f}\) an der Stelle \(x = 2\)
\[f(x) = \frac{4x + 4}{x^{2}}; \; D_{f} = \mathbb R \backslash \{0\}\]
\[P(2|f(2))\]
Der Ansatz für die Gleichung der Tangente \(T\) an der Stelle \(x = 2\) (im Punkt \(P(2|f(2))\)) kann mit der allgemeinen Geradengleichung oder mit der Tangentengleichung erfolgen.
1. Lösungsansatz: Allgemeine Geradengleichung
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[T \colon y = m_{T} \cdot x + t\]
Die erste Ableitung \(f'\) an der Stelle \(x = 2\) beschreibt die Steigung \(m_{T}\) der Tangente \(T\) an den Graphen der Funktion \(f\) im Punkt \(P(2|f(2))\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = f'(2)\]
Tangentensteigung \(m_{T}\) berechnen:
\(f'(x) = \dfrac{-4x - 8}{x^{3}}\) (vgl. Teilaufgabe c)
\[m_{T} = f'(2) = \dfrac{-4 \cdot 2 - 8}{2^{3}} = \dfrac{-16}{8} = -2\]
Damit ergibt sich die Gleichung der Tangente \(T\) zu:
\[T \colon y = -2x + t\]
\(y\)-Achsenabschnitt \(t\) der Tangente \(T\) bestimmen:
Die Tangente \(T\) berührt den Graphen der Funktion \(f\) im Punkt \(P(2|f(2))\; (P \in T)\). Setzt man die Koordinaten des Punktes \(P\) in die Gleichung der Tangente \(T\) ein, lässt sich damit der \(y\)-Achsenabschnit \(t\) bestimmen. Vorab ist noch der Funktionswert \(f(2)\) zu berechnen.
\[f(x) = \frac{4x + 4}{x^{2}}\]
\[f(2) = \frac{4 \cdot 2 + 4}{2^{2}} = \frac{12}{4} = 3\]
\[\Longrightarrow \quad P(2|3)\]
\[\begin{align*} P \in T \colon 3 &= (-2) \cdot 2 + t \\[0.8em] 3 &= -4 + t & &| +4 \\[0.8em] 7 &= t \end{align*}\]
Gleichung der Tangente \(T\) angeben:
\[T \colon y = -2x + 7\]
2. Lösungsansatz: Tangentengleichung
Gleichung einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\;(x_0|f(x_0)) \):
\[y = f'(x_{0}) \cdot (x - x_{0}) + f(x_{0})\]
\[P(2|f(2))\]
\[T \colon y = f'(2) \cdot (x - 2) + f(2)\]
Mit \(f'(2) = -2\) und \(f(2) = 3\) (vgl. 1. Lösungsansatz) folgt:
\[\begin{align*}T \colon y &= f'(2) \cdot (x - 2) + f(2) \\[0.8em] &= (-2) \cdot (x - 2) + 3 \\[0.8em] &= -2x + 4 + 3 \\[0.8em] &= -2x + 7 \end{align*}\]

