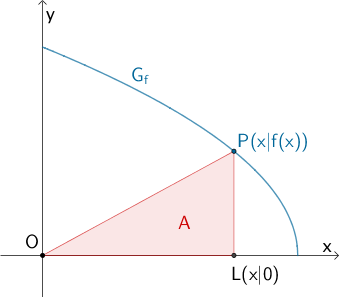
Die Abbildung zeigt den Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto 2\sqrt{6 - x}\) mit dem Definitionsbereich \(D_{f} = [0;6]\). Der Punkt \(P(x|f(x))\), der Lotfußpunkt \(L(x|0)\) des Lotes von \(P\) auf die \(x\)-Achse und der Koordinatenursprung \(O\) legen das Dreieck \(OLP\) fest.
Bestimmen Sie die Koordinaten des Punktes \(P\), sodass der Flächeninhalt \(A\) des Dreiecks \(OLP\) maximal ist.
\[f(x) = 2\sqrt{6 - x}; \; D_{f} = [0;6]\]
Hierbei handelt es sich um eine Extremwertaufgabe (vgl. Abiturskript - 1.5.7 Extremwertaufgaben).
Zunächst ist die Zielfunktion, welche den Flächeninhalt \(A\) des Dreiecks \(OLP\) in Abhängigkeit von \(x\) beschreibt, zu formulieren, und ein im Sachzusammenhang sinnvoller Definitionsbereich anzugeben.
Anschließend wird die Zielfunktion \(A(x)\) auf relative Extremstellen hin untersucht.
Zielfunktion \(A(x)\) formulieren:
Da der Punkt \(L\) der Lotfußpunkt des Lotes von Punkt \(P\) auf die \(x\)-Achse ist, ist das Dreieck \(OLP\) bei \(L\) rechtwinklig. Der Flächeninhalt \(A\) des Dreiecks \(OLP\) lässt sich somit durch die Längen der Katheten \([OL]\) und \([LP]\) ausdrücken.
Mit \(\overline{OL} = x\) und \(\overline{LP} = f(x)\) folgt:
\[\begin{align*} A(x) &= \frac{1}{2} \cdot \overline{OL}(x) \cdot \overline{LP}(x) \\[0.8em] &= \frac{1}{2} \cdot x \cdot f(x) \\[0.8em] &= \frac{1}{2} \cdot x \cdot 2\sqrt{6 - x} \\[0.8em] &= x\sqrt{6 - x} \end{align*}\]
Der Punkt \(P(x|f(x))\) mit \(f(x) = 2\sqrt{6 - x}\) und \(D_{f} = [0;6]\) liegt für \(x = 0\) auf der \(y\)-Achse und für \(x = 6\) auf der \(x\)-Achse, sodass jeweils kein Dreieck \(OLP\) mehr existiert. Es wird deshalb der im Sachzusammenhang sinnvolle Definitionsbereich \(D_{A} = \; ]0;6[\) festgelegt.
\[A(x) = x\sqrt{6 - x}; \; D_{A} = \; ]0;6[\]
Extremstelle von \(A(x)\) ermitteln:
Der Flächeninhalt \(A\) des Dreiecks \(OLP\) soll maximal sein. Die notwendige Bedingung für eine Extremstelle von \(A(x)\) lautet:
\[A'(x) = 0\]
Erste Ableitung \(A'\) bilden:
Die Funktion \(A(x)\) lässt sich mithilfe der Produktregel, der Kettenregel, der Ableitung einer Wurzelfunktion, der Ableitung einer Potenzfunktion sowie der Summregel ableiten. Als Alternative formuliert man die Wurzel mithilfe der Rechenregel für Potenzen \(\sqrt[n]{a^{m}} = a^{\frac{m}{n}}\) vorab in der Potenzschreibweise.
\[A(x) = x\sqrt{6 - x} = x(6 - x)^{\frac{1}{2}}\]
!. Möglichkeit: Wurzelausdruck ableiten
\[A(x) = x\sqrt{6 - x}\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*}A'(x) &= 1 \cdot \sqrt{6 - x} + x \cdot \frac{-1}{2\sqrt{6 - x}} \\[0.8em] &= \sqrt{6 - x} - \frac{x}{2\sqrt{6 - x}} & &| \; \text{gem. Nenner}\; 2\sqrt{6 - x}\; \text{bilden} \\[0.8em] &= \frac{\sqrt{6 - x} \cdot 2\sqrt{6 - x}}{2\sqrt{6 - x}} - \frac{x}{2\sqrt{6 - x}} \\[0.8em] &= \frac{2(6 - x) - x}{2\sqrt{6 - x}} \\[0.8em] &= \frac{12 - 3x}{2\sqrt{6 - x}} \\[0.8em] &= \frac{3(4 - x)}{2\sqrt{6 - x}}\end{align*}\]
2. Möglichkeit: Ableiten nach Umformulieren in die Potenzschreibweise
\[A(x) = x(6 - x)^{\frac{1}{2}}\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*}A'(x) &= 1 \cdot (6 - x)^{\frac{1}{2}} + x \cdot \frac{1}{2} \cdot (6 - x)^{-\frac{1}{2}} \cdot (-1) &&| \; a^{-n} = \frac{1}{a^{n}}; \; \sqrt[n]{a^{m}} = a^{\frac{m}{n}} \\[0.8em] &= \sqrt{6 - x} - \frac{x}{2\sqrt{6 - x}} & &| \; \text{gem. Nenner}\; 2\sqrt{6 - x}\; \text{bilden} \\[0.8em] &= \frac{\sqrt{6 - x} \cdot 2\sqrt{6 - x}}{2\sqrt{6 - x}} - \frac{x}{2\sqrt{6 - x}} \\[0.8em] &= \frac{2(6 - x) - x}{2\sqrt{6 - x}} \\[0.8em] &= \frac{12 - 3x}{2\sqrt{6 - x}} \\[0.8em] &= \frac{3(4 - x)}{2\sqrt{6 - x}}\end{align*}\]
Nullstelle von \(A'(x)\) berechnen:
Ein Quotient ist gleich Null, wenn der Zähler gleich Null ist.
\[\begin{align*}A'(x) = 0 \quad \Longrightarrow \quad 4 - x &= 0 &&| + x \\[0.8em] 4 = x \end{align*}\]
Nachweis, dass \(A(x)\) an der Stelle \(\x = 4) ein relatives Maximum besitzt:
\[A'(x) = \frac{3(4 - x)}{\underbrace{2\sqrt{6 - x}}_{>\,0}}\]
Der Zähler des Funtionsterms von \(A'(x)\) bestimmt den Vorzeichenwechsel von \(A'(x)\) in der Umgebung von \(x = 4\).
Da die Ableitungsfunktion \(A'(x)\) an der Stelle \(x = 4\) das Vorzeichen \(+\) nach \(-\) wechselt, hat die Funktion \(A(x)\) an der Stelle \(x = 4\) ein relatives Maximum.
\[\left. \begin{align*} &A'(x) > 0 \; \text{für} \; x < 4 \\[0.8em] &A(4) = 0 \\[0.8em] &A'(x) < 0 \; \text{für} \; x > 4 \end{align*} \right\} \enspace \Rightarrow \enspace \text{relatives Maximum}\; (4|A(4))\]
Berücksichtigung möglicher Randmaxima:
Bei Extremwertaufgaben ist es wichtig, den ermittelten Extremwert mit den Werten an den Definitionsrändern der Zielfunktion zu vergleichen, um mögliche Radextremwerte zu berücksichtigen.
In diesem Fall wurde \(x = 0\) und \(x = 6\) bereits bei der Wahl eines im Sachzusammenhang sinnvollen Definitionsbereichs ausgeschlossen, sodass es kein Randmaximum geben kann. Dies geht auch aus der Abbildung der Angabe hervor.
Also ist der Flächeninhalt des Dreiecks \(OLP\) an der Stelle \(x = 4\) mit \(A(4) = 4\cdot \sqrt{6 - 4} = 4\sqrt{2}\) FE (Flächeneinheiten) maximal.
Anmerkung:
Mit den Mitteln der Differentialrechnung werden die Ränder des Definitionsbereichs einer Zielfunktion nicht erfasst, weil die Zielfunktion selbst bei einem geschlossenen Definitionsbereich \([a;b]\) an den Rändern nicht differenzierbar ist. Der links- bzw. rechtsseitige Differentialquotient existiert nicht, d. h. die Zielfunktion ist an den Definitionsrändern nicht „ableitbar" (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit),
Lage des Punktes \(P(x|f(x))\) des Dreiecks \(OLP\) mit maximalem Flächeninhalt berechnen:
\[x = 4; \; f(x) = 2\sqrt{6 - x}\]
\[f(4) = 2 \cdot \sqrt{6 - 4} = 2\sqrt{2}\]
Mit \(P(4|2\sqrt{2})\) ist der Flächeninhalt des Dreiecks \(OLP\) maximal.

