Betrachtet wird die Aussage \(\displaystyle \int_{0}^{\pi} \sin(2x)\,dx = 0\).
Machen Sie ohne Rechnung anhand einer sorgfältigen Skizze plausibel, dass die Aussage wahr ist.
(3 BE)
Lösung zu Teilaufgabe 4a
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
Die Funktion \(h(x) = \sin (2x)\) ist gegenüber der Sinusfunktion \(f(x) = \sin x\) um den Faktor \(\frac{1}{2}\) in \(x\)-Richtung gestreckt (Stauchung).
Die Streckung (Stauchung) verändert die Periode \(p_h\) der Funktion \(h(x) = \sin(2x)\):
\[h(x) = \sin(2x) \quad \Longrightarrow \quad p_h = \frac{2\pi}{2} = \pi\]
Bestimmtes Integral als Flächenbilanz
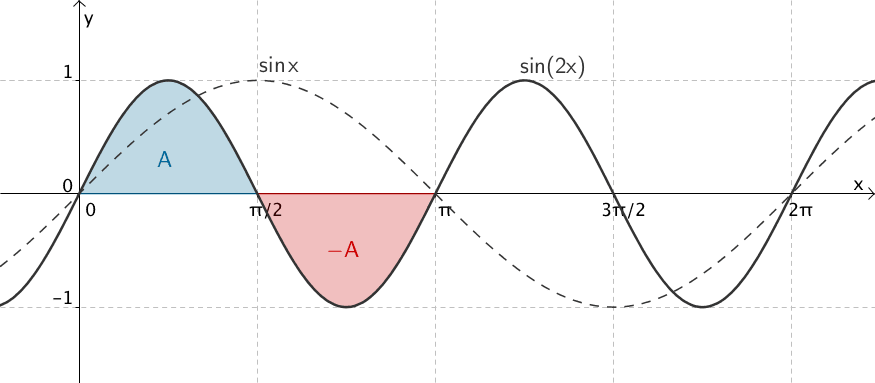
Das bestimmte Integral \(\int_{0}^{\pi} \sin (2x)\,dx\) gibt den Wert der Flächenbilanz an. Da es die Fläche oberhalb der \(x\)-Achse positiv und die Fläche unterhalb der \(x\)-Achse negativ zählt, ist die Flächenbilanz gleich Null.

