Die Seitenfläche \(PQRS\) liegt in einer Ebene \(F\). Bestimmen Sie, ohne zu rechnen, eine Gleichung von \(F\) in Normalenform; erläutern Sie Ihr Vorgehen.
(2 BE)
Lösung zu Teilaufgabe d
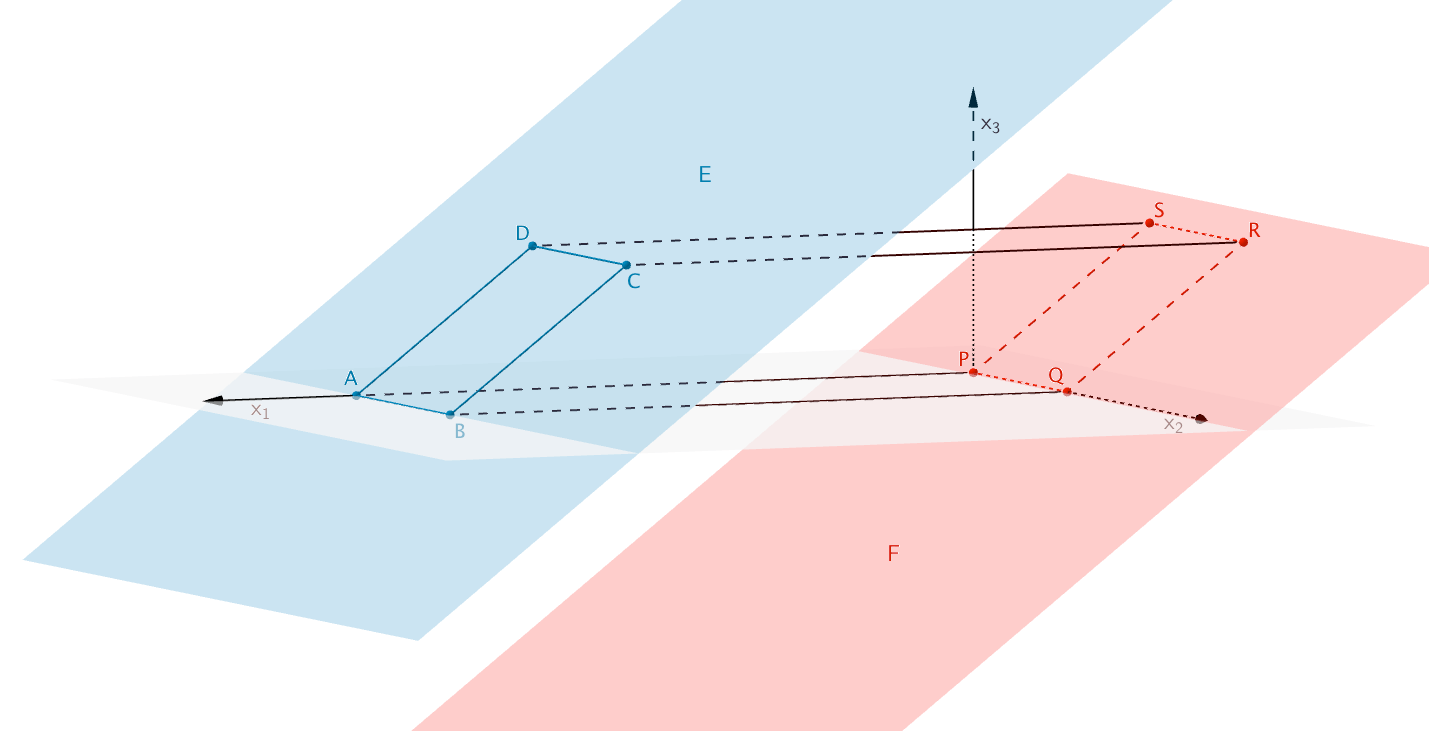
Die Seitenflächen \(ABCD\) und \(PQRS\) des Spats \(ABCDPQRS\) sind zueinander parallel. Folglich liegt die Ebene \(F\) parallel zur Ebene \(E\) und es gilt: \(\overrightarrow{n}_{F} = \overrightarrow{n}_{E}\).
Die Ebene \(F\) enthält den Koordinatenursprung \(P\,(0|0|0)\). Das bedeutet, dass der konstante Summand \(n_0\) der Ebenengleichung von \(F\) in Normalenform in Koordinatendarstellung gleich Null ist.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
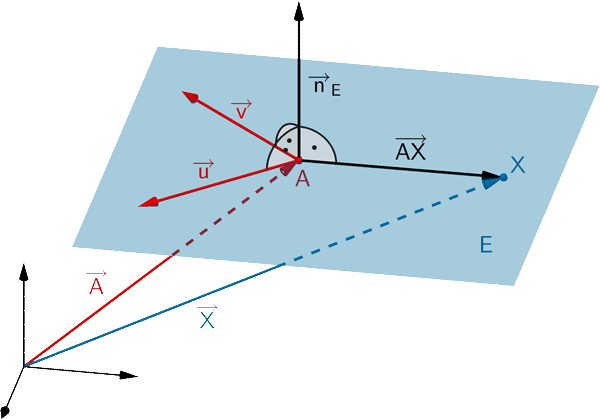
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E\,\colon\;3x_1 + 4x_3 - 84 = 0\]
\[F\,\colon\; n_1x_1 + n_2x_2 + n_3x_3 + n_0 = 0\]
\[\left. \begin{align*} &F \parallel E \quad \Longrightarrow \quad \overrightarrow{n}_F = \overrightarrow{n}_E \\[0.8em] &P\,(0|0|0) \in F \quad \Longrightarrow \quad n_0 = 0 \end{align*} \right\} \enspace \Rightarrow \enspace F\,\colon\; 3x_1 + 4x_3 = 0\]


