Durch die Punkte \(A\) und \(B\) verläuft die Gerade \(g\).
Betrachtet werden Geraden, für welche die Bedingungen I und II gelten:
I Jede dieser Geraden schneidet die Gerade \(g\) orhogonal.
II Der Abstand jeder dieser Geraden vom Punkt \(A\) beträgt 3.
Ermitteln Sie eine Gleichung für eine dieser Geraden.
(3 BE)
Lösung zu Teilaufgabe 2b
Orthogonale Geraden im Raum, Einheitsvektor, Schnittpunkt Gerade - Ebene, Schnittpunkte Gerade - Kugel
\[g = AB\]
Es sei \(h\) eine der Geraden, für die die Bedingungen I und II gelten.
\(h \perp g\), \(d(h;A) = 3\)
\(A(-2|1|4)\), \(B(-4|0|6)\) (vgl. Teilaufgabe 2a)
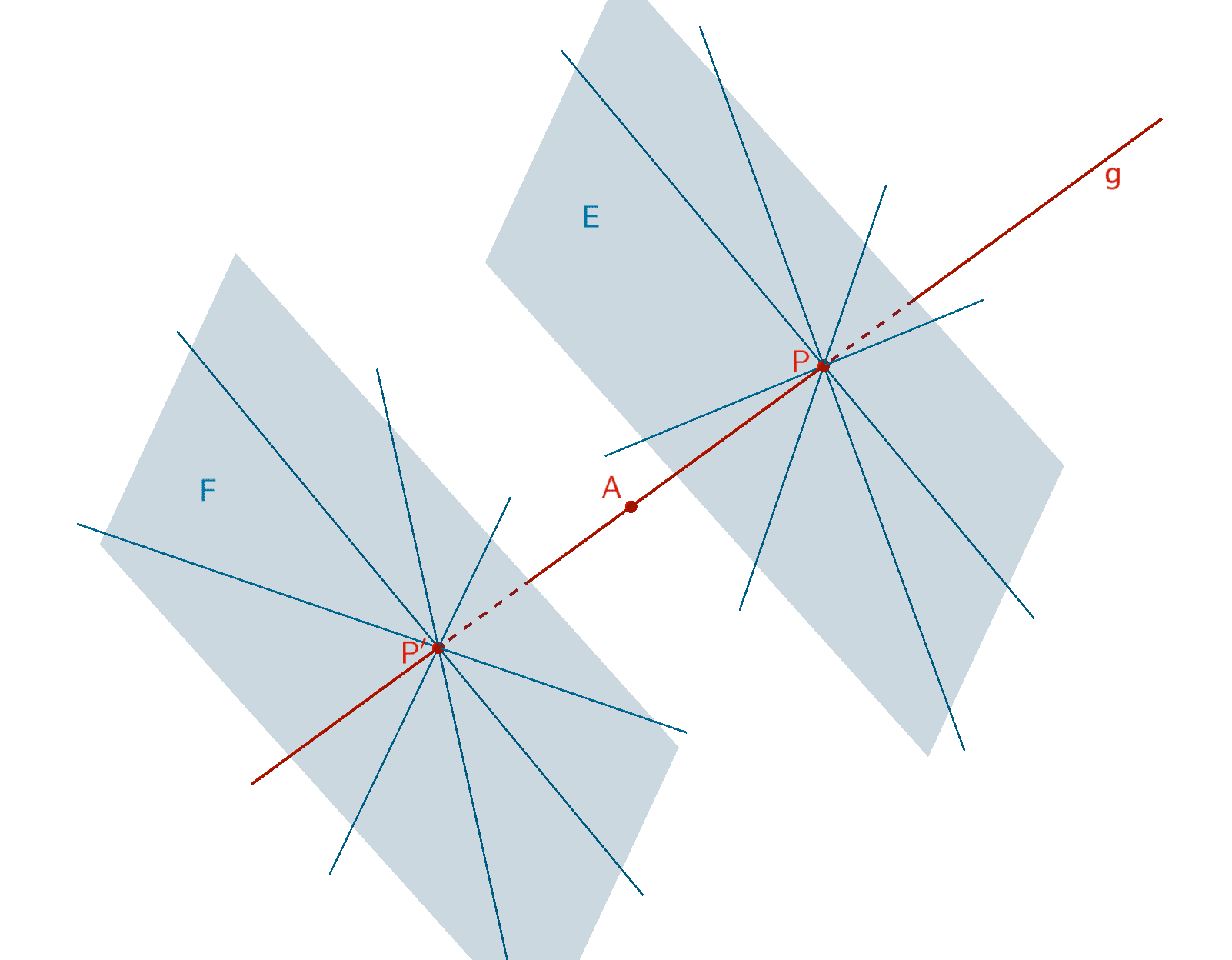
Es gibt unendlich viele Geraden, welche die Gerade \(g\) im Punkt \(P\) bzw. \(P'\) im Abstand \(d(P;A) = d(P';A) = 3\) orthogonal (senkrecht) schneiden. Die Geraden liegen in zwei zur Geraden \(g\) orthogonalen Ebenen \(E\) bzw. \(F\).
Gleichung der Geraden \(g\):
Die Gerade \(g\) verläuft durch die Punkte \(A\) und \(B\). Wählt man beispielsweise den Punkt \(A\) als Aufpunkt und den Verbindungsvektor \(\overrightarrow{AB}\) als Richtungsvektor für die Gleichung der Geraden \(g\), ergibt sich folgende Geradengleichung:
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}; \; \lambda \in \mathbb R\]
Gleichung einer Geraden \(h \perp g\) mit \(d(h;A) = 3\):
Es sei \(\overrightarrow{v}\) der Richtungsvektor einer Geraden \(h \perp g\).
Mit \(d(h;A) = d(P;A) = d(P';A) = 3\) kommen als mögliche Aufpunkte einer Geraden \(h\) die Punkte \(P\) und \(P'\) in Frage.
\[h \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{v}; \; \mu \in \mathbb R\]
oder
\[h \colon \overrightarrow{X} = \overrightarrow{P'} + \tau \cdot \overrightarrow{v}; \; \tau \in \mathbb R\]
Möglicher Richtungsvektor \(\overrightarrow{v}\) der Gleichung einer Geraden \(h \perp g\) (Bedingung I)
Entsprechend der Bedingung I: \(h \perp g\), sind die Richtungsvektoren \(\overrightarrow{v}\) und \(\overrightarrow{AB}\) einer geraden \(h\) und der Geraden \(g\) zueinander senkrecht. Folglich muss das Skalarprodukt der Richtungsvektoren gleich Null sein.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{v} \perp \overrightarrow{AB} \quad \Longleftrightarrow \quad \overrightarrow{v} \circ \overrightarrow{AB} = 0\]
Richtungsvektor \(\overrightarrow{AB}\) der Geraden \(g\) bestimmen:
\(A(-2|1|4)\), \(B(-4|0|6)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} - \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} = \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix}\]
Möglichen Richtungsvektor \(\overrightarrow{v}\) einer Geraden \(h \perp g\) finden:
\[\begin{align*}\overrightarrow{v} \circ \overrightarrow{AB} &= 0 \\[0.8em] \overrightarrow{v} \circ \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} &= 0 \end{align*}\]
Ein möglicher Richtungsvektor \(\overrightarrow{v}\) lässt sich durch „Probieren" finden.
Beispielsweise erfüllt der Richtungsvektor \(\overrightarrow{v} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}\) diese Gleichung, denn es gilt:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \circ \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} = 1 \cdot (-2) + 0 \cdot (-1) + 1 \cdot 2 = 0\]
Will man mathematisch vorgehen, löst man die Gleichung \(\begin{pmatrix} v_{1} \\ v_{2} \\ v_{3} \end{pmatrix} \circ \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} = 0\), indem man zwei der drei unbekannten Koordinaten \(v_{1}\), \(v_{2}\) und \(v_{3}\) frei wählt, und die dritte Koordinate entsprechen bestimmt.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \begin{pmatrix} v_{1} \\ v_{2} \\ v_{3} \end{pmatrix} \circ \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} &= 0 \\[0.8em] v_{1} \cdot (-2) + v_{2} \cdot (-1) + v_{3} \cdot 2 &= 0 \\[0.8em] -2v_{1} -v_{2} +2v_{3} &= 0 \end{align*}\]
Zwei Koordinaten frei wählen, beispielweise \(v_{1} = 1\) und \(v_{2} = 0\).
\[\begin{align*}\Longrightarrow \quad -2 \cdot 1 - 0 + 2 \cdot v_{3} &= 0 \\[0.8em] -2 + 2v_{3} &= 0 & &| + 2 \\[0.8em] 2v_{3} &= 2 & &| : 2 \\[0.8em] v_{3} &= 1 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{v} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}\]
Damit ergibt sich die Gleichung einer Geraden \(h \perp g\) mit \(d(h;A) = 3\) zu:
\[h \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]
oder
\[h \colon \overrightarrow{X} = \overrightarrow{P'} + \tau \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \tau \in \mathbb R\]
Mögliche Aufpunkte der Gleichung einer Geraden \(h\) mit \(d(h;A) = 3\) (Bedingung II)
\[d(h;A) = d(P;A) = d(P';A) = 3\]
1. Lösungsansatz: Einheitsvektor \(\overrightarrow{AB}^{0}\)
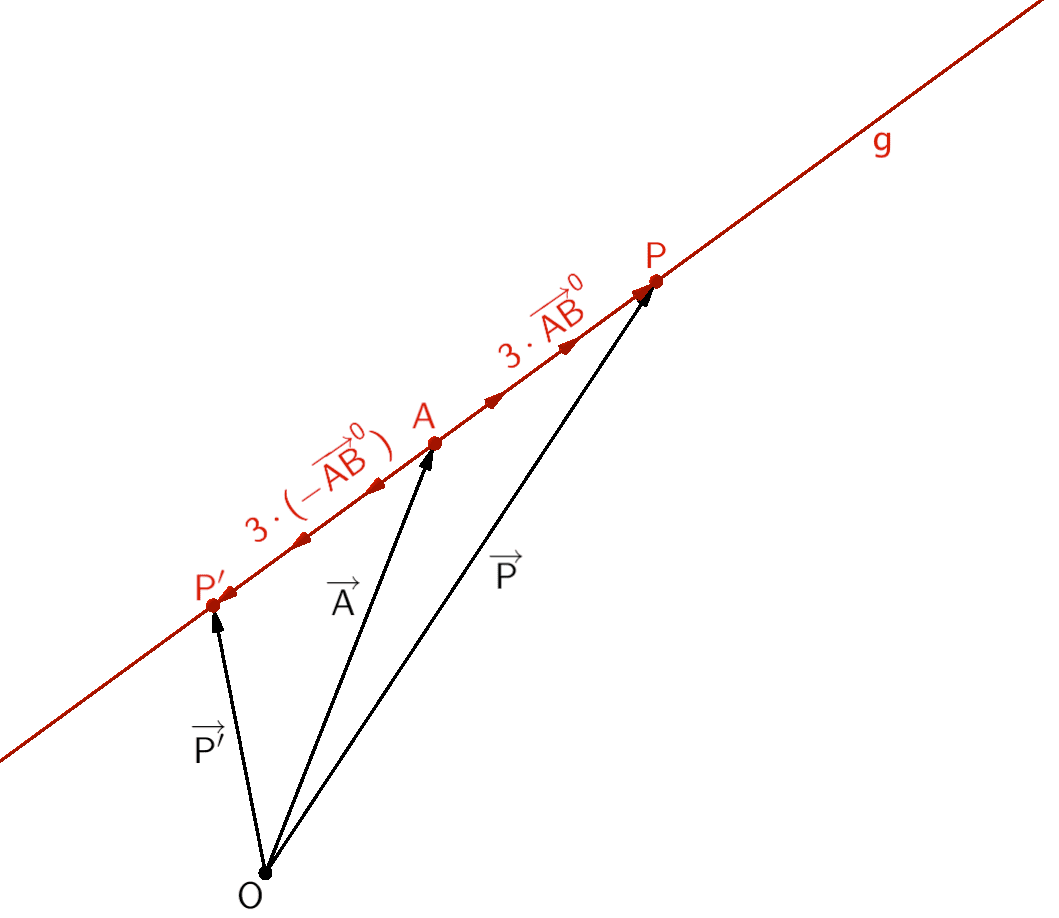
Unter Verwendung des Einheitsvektors \(\overrightarrow{AB}^{0}\) des Richtungsvektors \(\overrightarrow{AB}\) der Geraden \(g\) lassen sich die Koordinaten der Punkte \(P\) und \(P'\) durch Vektoraddition bzw. -subtraktion berechnen.
\[\overrightarrow{P} = \overrightarrow{A} + 3 \cdot \overrightarrow{AB}^{0}\]
\[\overrightarrow{P'} = \overrightarrow{A} - 3 \cdot \overrightarrow{AB}^{0}\]
Einheitsvektor \(\overrightarrow{AB}^{0}\) bestimmen:
Einheitsvektor (vgl. Merkhilfe)
\[\overrightarrow{a}^0 = \frac{\overrightarrow{a}}{\vert \overrightarrow{a} \vert}\]
Vektoren mit der Länge 1 heißen Einheitsvektoren.
\(\overrightarrow{AB} = \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix}\) (vgl. Richtungsvektor der Geraden \(g\))
\[\begin{align*} \overrightarrow{AB}^{0} &= \frac{\overrightarrow{AB}}{\vert \overrightarrow{AB} \vert} \\[0.8em] &= \frac{\begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix}}{\left| \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} \right|} \\[0.8em] &= \frac{\begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix}}{\sqrt{(-2)^{2} + (-1)^{2} + 2^{2}}} \\[0.8em] &= \frac{1}{3} \cdot \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} \end{align*}\]
Koordinaten des Punktes \(P\) bzw. des Punktes \(P'\) berechnen:
\[A(-2|1|4)\]
\[\overrightarrow{P} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} + 3 \cdot \frac{1}{3} \cdot \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} = \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} = \overrightarrow{B}\]
\[\overrightarrow{P'} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} - 3 \cdot \frac{1}{3} \cdot \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix}\]
Gleichung einer Geraden \(h \perp g\) mit \(d(h;A) = 3\) formulieren:
\[h \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]
oder
\[h \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \tau \in \mathbb R\]
2. Lösungsansatz: Schnittpunkte einer Kugel \(K\) und der Geraden \(g\)
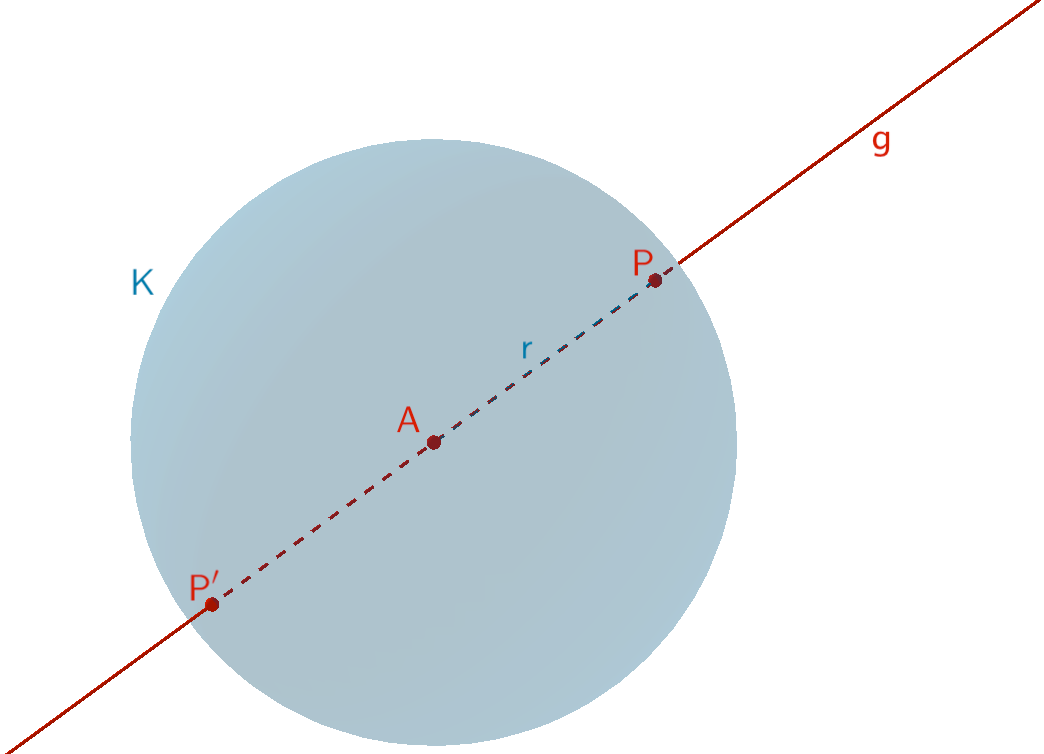
Die Gerade \(g\) schneidet die Kugel \(K\) mit dem Mittelpunkt \(A\) und dem Radius \(r = d(P;A) = d(P';A) = 3\) in den Punkten \(P\) und \(P'\).
Gleichung der Kugel \(K\) mit dem Mittelpunkt \(A\) und dem Radius \(r = 3\):
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\(A(-2|1|4)\), \(r = 3\)
\[K \colon (x_{1} - a_{1} )^{2} + (x_{2} - a_{2} )^{2} + (x_{3} - a_{3} )^{2} = 3^{2}\]
\[K \colon (x_{1} + 2)^{2} + (x_{2} - 1)^{2} + (x_{3} - 4)^{2} = 9\]
Schnittpunkte der Geraden \(g\) und der Kugel \(K\) berechnen:
\[g \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[K \colon (x_{1} + 2)^{2} + (x_{2} - 1)^{2} + (x_{3} - 4)^{2} = 9\]
Die Schnittpunkte \(P\) und \(P'\) der Geraden \(g\) und der Kugel \(K\) erhält man, indem man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Gleichung der Kugel \(K\) einsetzt und die Gleichung nach dem Parameter \(\lambda\) auflöst. Setzt man die errechneten Parameterwerte für \(\lambda\) in die Gleichung der Geraden \(g\) ein, liefern die Gleichungen die Ortsvektoren \(\overrightarrow{P}\) und \(\overrightarrow{P'}\).
\[\begin{align*} g \cap K \colon (-2 - 2\lambda + 2)^{2} + (1 - \lambda - 1)^{2} + (4 - 4\lambda - 4)^{2} &= 9 \\[0.8em] 4 \lambda^{2} + \lambda^{2} + 4\lambda^{2} &= 9 \\[0.8em] 9\lambda^{2} &= 9 & &| : 9 \\[0.8em] \lambda^{2} &= 1 & &| \; \sqrt{\enspace} \\[0.8em] \lambda_{1,2} &= \pm 1 \end{align*}\]
Parameterwerte \(\lambda = 1\) bzw. \(\lambda = -1\) in die Geradengleichung von \(g\) einsetzen:
\[\overrightarrow{P} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} + 1 \cdot \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} = \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} = \overrightarrow{B}\]
\[\overrightarrow{P} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} - 1 \cdot \begin{pmatrix} -2 \\ -1 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix}\]
Gleichung einer Geraden \(h \perp g\) mit \(d(h;A) = 3\) formulieren:
\[h \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 0 \\ 6 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]
oder
\[h \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} + \tau \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}; \; \tau \in \mathbb R\]

