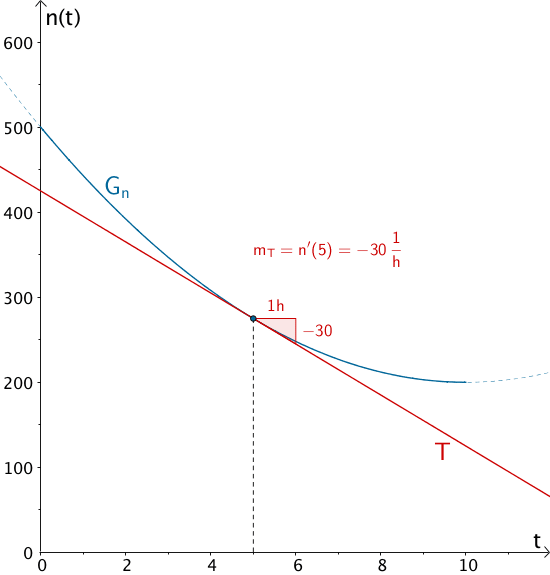
Ermitteln Sie den Zeitpunkt nach Beginn der Messung, zu dem die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft \(-30\frac{\textsf{1}}{\textsf{h}}\) beträgt.
(2 BE)
Lösung zu Teilaufgabe 4b
Momentane Änderungsrate im Sachzusammenhang
\[n(t) = 3t^{2} - 60t + 500\]
\[t \in [0;10]\]
Die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft zu einem bestimmten Zeitpunkt \(t\) entspricht der Steigung \(m_{T}\) einer gedachten Tangente \(T\) im Punkt \((t|n(t))\) des Graphen \(G_{n}\) der Funktion \(n(t)\) (Einheit: \(\frac{1}{\sf{h}}\)).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Die erste Ableitung \(n'(t)\) der Funktion \(n(t)\) beschreibt die Steigung \(m_{T}\) der Tangente \(T\) im Punkt \((t|n(t))\). Das heißt, im Sachzusammenhang beschreibt die erste Ableitung \(n'(t)\) die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft. Sie gibt für einen betrachteten Zeitpunkt \(t\) die momentane Änderung der Anzahl der Pollen pro Stunde in einem Kubikmeter Luft an (Zunahme: positive momentane Änderungsrate, Abnahme: negative momentane Änderungsrate).
Differentialquotient oder lokale bzw. momentane Änderungsrate
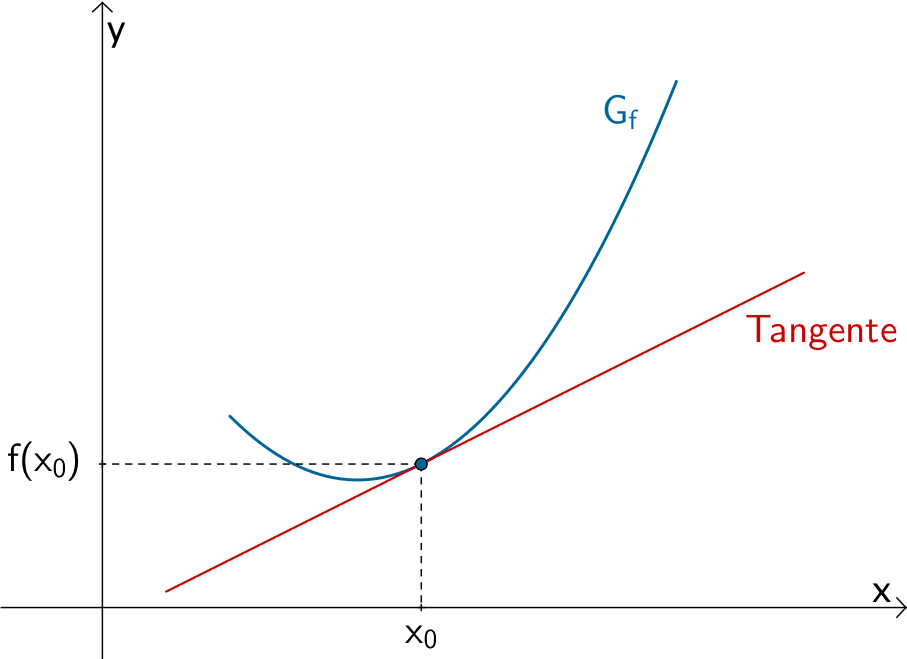
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Gesucht ist der Zeitpunkt \(t\) zu dem die momentane Änderungsrate \(n'(t)\) den Wert \(-30\,\frac{1}{\sf{h}}\) annimmt.
\[\Longrightarrow \quad n'(t) = -30\]
Erste Ableitung \(n'\) der Funktion \(n\) bilden:
Die erste Ableitung \(n'\) der Funktion \(n\) wird mithilfe der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel formuliert.
\[n(t) = 3t^{2} - 60t + 500\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} n'(t) &= 3 \cdot 2 \cdot t - 60 + 0 \\[0.8em] &= 6t - 60 \end{align*}\]
Zeitpunkt \(t\) ermitteln:
\[\begin{align*} n'(t) &= -30 \\[0.8em] 6t - 60 &= -30 & &| + 60 \\[0.8em] 6t &= 30 & &| : 6 \\[0.8em] t &= 5 \end{align*}\]
Fünf Stunden nach Beginn der Messung nimmt die Anzahl der Pollen in einem Kubikmeter Luft um 30 Pollen pro Stunde ab.