Zeigen Sie, dass \(G_{f}\) genau einen Wendepunkt \(W\) besitzt, und bestimmen Sie dessen Koordinaten sowie die Gleichung der Tangente an \(G_{f}\) im Punkt \(W\).
(zur Kontrolle: \(x\)-Koordinate von \(W\): \(e\))
(6 BE)
Teilaufgabe 1b
Lösung zu Teilaufgabe 1b
Nachweis des Wendepunkts \(W\)
Die notwendige Bedingung für einen Wendepunkt von \(G_{f}\) lautet:
\[f''(x) = 0\]
Zweite Ableitung \(f''\) bilden
Die zweite Ableitung \(f''\) kann mithilfe der Quotientenregel gebildet werden.
\[f'(x) = \frac{4}{x} \cdot \ln{x} = 4 \cdot \frac{\textcolor{#0087c1}{\ln{x}}}{\textcolor{#cc071e}{x}}\]
\[\begin{align*} f''(x) &= 4 \cdot \left( \frac{\textcolor{#0087c1}{\frac{1}{x}} \cdot \textcolor{#cc071e}{x} - \textcolor{#0087c1}{\ln{x}} \cdot \textcolor{#cc071e}{1}}{\textcolor{#cc071e}{x^{2}}} \right) \\[0.8em] &= 4 \cdot \left( \frac{1 - \ln{x}}{x^{2}} \right) \\[0.8em] &= \frac{4}{x^{2}} \cdot (1 - \ln{x}) \end{align*}\]
Nullstelle von \(f''(x)\) bestimmen:
\[\begin{align*} f''(x) &= 0 \\[0.8em] \frac{4}{x^{2}} \cdot (1 - \ln{x}) &= 0 &&| \cdot x^{2} \\[0.8em] 4 \cdot(1 - \ln{x}) &= 0 &&| : 4 \\[0.8em] 1 - \ln{x} &= 0 &&| + \ln{x} \\[0.8em] 1 &= \ln{x} &&| \; e^{(\dots)} \\[0.8em] e^{1} &= e^{\ln{x}} &&| \; e^{\ln{x}} = x \\[0.8em] e &= x \end{align*}\]
Alternative: Nach dem Satz vom Nullprodukt ist ein Produkt genau dann gleich Null, wenn einer der Faktoren gleich Null ist.
\[\begin{align*} f''(x) &= 0 \\[0.8em] \underbrace{\frac{4}{x^{2}}}_{\Large{\neq\,0}} \cdot (1 - \ln{x}) &= 0 \\[0.8em] \Longrightarrow \quad 1 - \ln{x} &= 0 &&| + \ln{x} \\[0.8em] 1 &= \ln{x} &&| \; e^{(\dots)} \\[0.8em] e^{1} &= e^{\ln{x}} &&| \; e^{\ln{x}} = x \\[0.8em] e &= x \end{align*}\]
\(x = e\) ist einzige mögliche Wendestelle.
Nun ist noch der Vorzeichenwechsel von \(f''(x)\) an der Stelle \(x = e\) nachzuweisen, Hierfür eignet sich eine Krümmungstabelle. Als Aternative kann mithilfe der dritten Ableitung \(f'''\) nachgewiesen werden, dass \(f'''(e) \neq 0\) gilt.
1. Möglichkeit: Krümmungstabelle
\(f''(x) = \underbrace{\dfrac{4}{x^{2}}}_{\Large{>\,0}} \cdot (1 - \ln{x})\) mit \(x \in \mathbb R^{+}\)
Der Faktor \((1 - \ln{x})\) bestimmt den Vorzeichenwechsel von \(f''(x)\) an der Stelle \(x = e\).
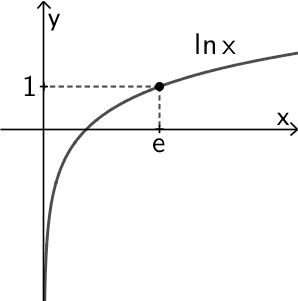
Für \(0 < x < e\) gilt \(\ln{x} < 1\) und für \(x > e\) gilt \(\ln{x} > 1\).
| \(x\) | \(0 < x < e\) | \(e\) | \(x > e\) |
| \(\dfrac{4}{x^{2}}\) | \(+\) | \(+\) | \(+\) |
| \((1 - \ln{x})\) | \(+\) | \(0\) | \(-\) |
| \(f''(x)\) | \(\textcolor{#0087c1}{\Large{+}}\) | \(0\) | \(\textcolor{#cc071e}{\Large{-}}\) |
| \(G_{f}\) | \(\style{display: inline-block; transform:rotate(0.5turn);}{\Large \textcolor{#0087c1}{\curvearrowleft}}\) | \(W(e|0)\) | \(\Large \textcolor{#cc071e}{\curvearrowright}\) |
Aus der Angabe zu Teilaufgabe 1a ist die Nullstelle \(x = e\) bekannt. \(G_{f}\) hat also genau den einen Wendepunkt \(W(e|0)\).
2. Möglichkeit: Nachweiß des Wendepunkts mithilfe der dritten Ableitung
Anmerkung:
Diese Möglichkeit weist zwar den Wendepunkt nach, sie ist aber zeitaufwendiger. Grundsätzlich hat diese Methode den Nachteil, dass sie das Krümmungsverhalten des zu untersuchenden Graphen nicht erfasst.
Dritte Ableitung \(f'''\) bilden
Die dritte Ableitung \(f'''\) kann mithilfe der Quotientenregel gebildet werden.
\[f''(x) = \frac{4}{x^{2}} \cdot (1 - \ln{x}) = 4 \cdot \frac{\textcolor{#0087c1}{1 - \ln{x}}}{\textcolor{#cc071e}{x^{2}}}\]
\[\begin{align*} f'''(x) &= 4 \cdot \left[ \frac{\textcolor{#0087c1}{(0 - \frac{1}{x})} \cdot \textcolor{#cc071e}{x^{2}} - \textcolor{#0087c1}{(1 - \ln{x})} \cdot \textcolor{#cc071e}{2x}}{\textcolor{#cc071e}{\left(x^{2}\right)^{2}}} \right] \\[0.8em] &= 4 \cdot \left[ \frac{-x - 2x(1 - \ln{x})}{x^{4}} \right] &&| \; x\;\text{ausklammern und kürzen} \;(x \in \mathbb R^{+}) \\[0.8em] &= 4 \cdot \left[ \frac{\cancelto{1}{x}(-1 - 2(1 - \ln{x}))}{\cancelto{x^{3}}{x^{4}}} \right] \\[0.8em] &= 4 \cdot \left( \frac{-1 - 2 + 2\ln{x}}{x^{3}}\right) \\[0.8em] &= \frac{4}{x^{3}} \cdot (2\ln{x} - 3)\end{align*}\]
\[f'''(e) = \frac{4}{e^{3}} \cdot (2\ln{e} - 3) = \frac{4}{e^{3}} \cdot (2 \cdot 1 - 3) = -\frac{4}{e^{3}}\]
\[\Longrightarrow \quad f'''(e) \neq 0 \quad \Longrightarrow \quad W(e|0)\]
Gleichung der Wendetangente
Der Ansatz der Gleichung der Wendetangente \(w\) kann mit der allgemeinen Geradengleichung erfolgen.
\[w \colon y = mx + t\]
Steigung der Wendetangente berechnen:
Die erste Ableitung \(f'\) beschreibt die Steigung einer Tangente an den Graphen von \(f\). Also beschreibt \(f'(e)\) die Steigung der Wendetangente \(w\) im Wendepunkt \(W(e|0)\).
\(f'(x) = \dfrac{4}{x} \cdot \ln{x}\) (vgl. Teilaufgabe a)
\[m = f'(e) = \frac{4}{e} \cdot \ln{e} = \frac{4}{e} \cdot 1 = \frac{4}{e}\]
\[\Longrightarrow \quad w \colon y = \frac{4}{e}x + t\]
\(y\)-Achsenabschnitt \(t\) berechnen:
Hierfür werden die Koordinaten des Wendepunktes \(W(e|0)\) in die Gleichung der Wendetangente \(w\) eingesetzt und diese nach \(t\) aufgelöst.
\[\begin{align*} W(e|0) \in w \colon 0 &= \frac{4}{e} \cdot e + t \\[0.8em] 0 &= 4 + t &&| - 4 \\[0.8em] - 4 &= t \end{align*}\]
\[\Longrightarrow \quad w \colon y = \frac{4}{e}x - 4\]
