Ermitteln Sie mithilfe der Abbildung die \(x\)-Koordinaten der Schnittpunkte der Graphen von \(f\) und \(g\).
(3 BE)
Lösung zu Teilaufgabe 4b
\(g(x) = \dfrac{1}{f(x)}; \; x \neq 1\) (vgl. Teilaufgabe 4a)
Der Ansatz für die Bestimmung der \(x\)-Koordinaten der Schnittpunkte der Graphen von \(f\) und \(g\) lautet:
\[\begin{align*} f(x) &= g(x) \\[0.8em] f(x) &= \frac{1}{f(x)} &&| \cdot f(x) \\[0.8em] [f(x)]^{2} &= 1 &&| \; \sqrt{\quad} \\[0.8em] \textcolor{#e9b509}{f(x)} &\textcolor{#e9b509}{=} \textcolor{#e9b509}{\pm 1} \end{align*}\]
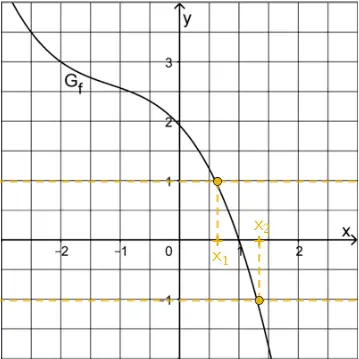
Mithilfe der Abbildung ergeben sich die \(x\)-Koordinaten der Schnittpunkte der Graphen von \(f\) und \(g\) somit zu \(\textcolor{#e9b509}{x_{1} \approx 0{,}6}\) und \(\textcolor{#e9b509}{x_{2} \approx 1{,}3}\).

