Ebenengleichung in Normalenform

In einem kartesischen Koordinatensystem legen die Punkte \(A(6|3|3)\), \(B(3|6|3)\) und \(C(3|3|6)\) das gleichseitige Dreieck \(ABC\) fest.

Ermitteln Sie eine Gleichung der Ebenen \(E\), in der das Dreieck \(ABC\) liegt, in Normalenform.

(mögliches Ergebnis: \(E \colon x_{1} + x_{2} + x_{3} - 12 = 0\))

(4 BE)

Die Punkte \(P\) und \(Q\) liegen symmetrisch zu einer Ebene \(F\). Ermitteln Sie eine Gleichung von \(F\).

(3 BE)

Die Punkte \(A\), \(B\), \(E\) und \(F\) liegen in der Ebene \(L\). Ermitteln Sie eine Gleichung von \(L\) in Normalenform.

(zur Kontrolle: \(L \colon 2x_{1} + 2x_{2} + 3x_{3} - 12 = 0\))

(4 BE)

Gegeben ist die Ebene \(E \colon 2x_{1} + x_{2} - 2x_{3} = -18\).

Der Schnittpunkt von \(E\) mit der \(x_{1}\)-Achse, der Schnittpunkt von \(E\) mit der \(x_{2}\)-Achse und der Koordinatenursprung sind die Eckpunkte eines Dreiecks. Bestimmen Sie den Flächeninhalt dieses Dreiecks.

(2 BE)

Von der Boje aus taucht der Fotograf senkrecht bezüglich der Wasseroberfläche nach unten bis zu einer Stelle, deren Abstand zum Meeresboden genau drei Meter beträgt und im Modell durch den Punkt \(K\) dargestellt wird.

Bestimmen Sie rechnerisch, welche Tiefe unter der Wasseroberfläche der Fotograf bei diesem Tauchvorgang erreicht.

(5 BE)

Ermitteln Sie die Koordinaten des Vektors, der sowohl ein Normalenvektor von \(E\) als auch der Ortsvektor eines Punktes der Ebene \(E\) ist.

(3 BE)

Bestimmen Sie die Koordinaten des Punkts \(C\). Ermitteln Sie eine Gleichung der Ebene \(E\), in der das Rechteck \(ABCD\) liegt, in Normalenform.

(mögliches Teilergebnis: \(E\colon 4x_{1} + 5x_{3} - 20 = 0\))

(5 BE)

An den betrachteten geraden Abschnitt der Achterbahn schließt sich - in Fahrtrichtung gesehen - eine Rechtskurve an, die im Modell durch einen Viertelkreis beschrieben wird, der in der Ebene \(E\) verläuft und den Mittelpunkt \(M \left( 0|3\sqrt{2}|2 \right)\) hat.

Das Lot von \(M\) auf \(g\) schneidet \(g\) im Punkt \(B\). Im Modell stellt \(B\) den Punkt der Achterbahn dar, in dem der gerade Abschnitt endet und die Kurve beginnt. Bestimmen Sie die Koordinaten von \(B\) und berechnen Sie den Kurvenradius im Modell.

(Teilergebnis: \(B\left( -1|2\sqrt{2}|3 \right)\)) 

(5 BE)

Die \(x_{1}x_{2}\)-Ebene beschreibt modellhaft eine horizontale Fläche, auf der eine Achterbahn errichtet wurde. Ein gerader Abschnitt der Bahn beginnt im Modell im Punkt \(A\) und verläuft entlang der Geraden \(g\). Der Vektor \(\displaystyle \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\) beschreibt die Fahrtrichtung auf diesem Abschnitt.

Berechnen Sie im Modell die Größe des Winkels, unter dem dieser Abschnitt der Achterbahn gegenüber der Horizontalen ansteigt.

(3 BE)

Bestimmen Sie die Koordinaten von \(N\) und \(L\).

(Teilergebnis: \(N\,(7{,}2|8|7)\))

(4 BE)

Die Ebene \(E \colon 3x_{1} + 2x_{2} + 2x_{3} = 6\) enthält einen Punkt, dessen drei Koordinaten übereinstimmen. Bestimmen Sie diese Koordinaten.

(2 BE)

Der Punkt \(L\), der vertikal über dem Mittelpunkt der Kante \([A_{1}A_{2}]\) liegt, veranschaulicht im Modell die Position einer Flutlichtanlage, die 12 m über der Grundfläche angebracht ist. Die als punktförmig angenommene Lichtquelle beleuchtet - mit Ausnahme des Schattenbereichs in der Nähe der Hallenwände - das gesamte Gelände um die Halle.

Die Punkte \(L\), \(B_{2}\) und \(B_{3}\) legen eine Ebene \(F\) fest. Ermitteln Sie eine Gleichung von \(F\) in Normalenform.

(zur Kontrolle: \(F \colon 3x_{1} + x_{2} + 5x_{3} - 90 = 0\))

(5 BE)

Bestimmen Sie eine Gleichung der Ebene \(E\) in Koordinatenform und zeigen Sie, dass die Gerade \(g\) in \(E\) liegt.

(zur Kontrolle: \(E \colon 2x_1 - x_2 + 2x_3 + 35 = 0\))

(5 BE)

Untersuchen Sie rechnerisch, ob die Kugel mit Mittelpunkt \(Z\,(1|6|3)\) und Radius 7 die Ebene \(E\) schneidet.

(4 BE)

Gegeben ist die Ebene \(E\,\colon \, 3x_2 + 4x_3 = 5\).

Beschreiben Sie die besondere Lage von \(E\) im Koordinatensystem.

(1 BE)

Die Abbildung zeigt einen Würfel der Kantenlänge 6. Die Koordinaten der Eckpunkte \(A\,(0|0|0)\), \(D\,(0|6|0)\) und \(G\,(6|6|6)\) sind gegeben.

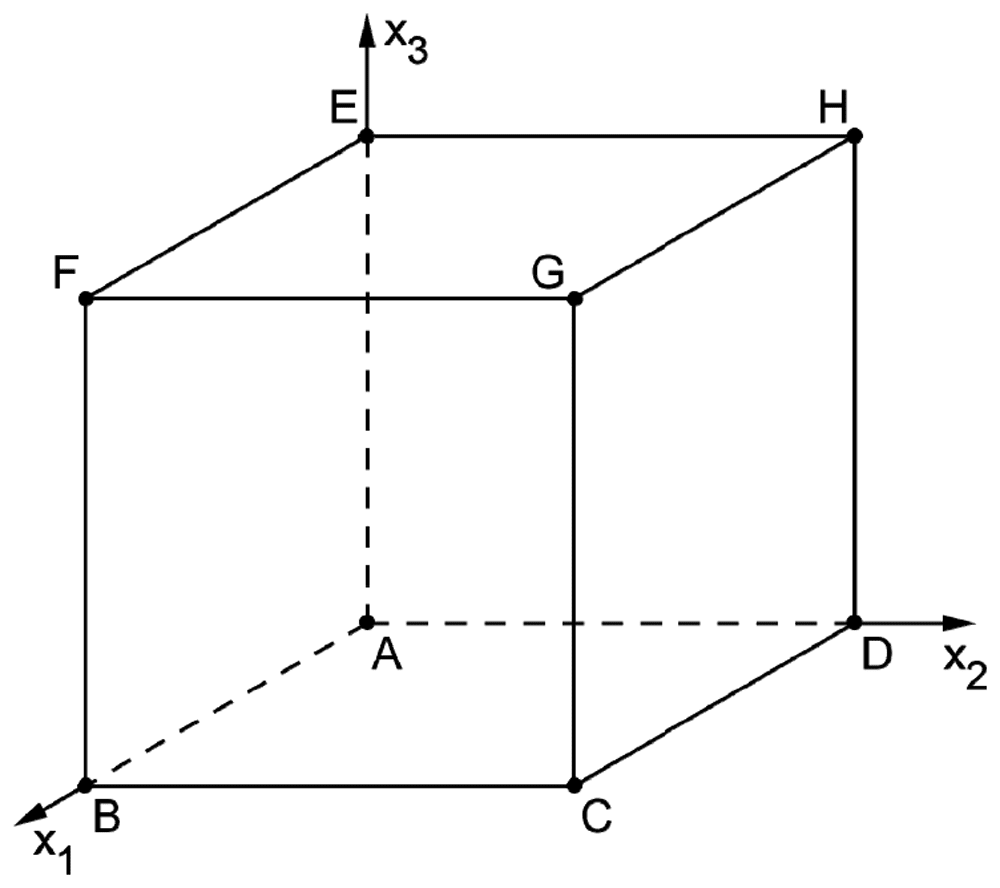
Die Punkte \(B\), \(E\) und \(G\) liegen in einer Ebene \(L\). Bestimmen Sie eine Gleichung von \(L\) in Normalenform. Zeichnen Sie die Figur, in der die Ebene \(L\) den Würfel schneidet, in die Abbildung ein.

(mögliches Ergebnis: \(L\,\colon\; x_1 - x_2 + x_3 = 6\))

(5 BE)

Eine Radarstation, deren Position im Modell durch den Punkt \(R\,(20|30|0)\) veranschaulicht wird, erfasst alle Objekte im Luftraum bis zu einer Entfernung von 50 km. Berechnen Sie die Länge der Flugstrecke von \(F_2\) in dem vom Radar erfassten Bereich.

(6 BE)

Die Abbildung zeigt den Körper \(ABCDEF\) mit \(A(6|3|0)\), \(B(0|6|0)\), \(C(3|0|0)\), \(D(6|3|6)\), \(E(0|6|6)\) und \(F(3|0|12)\).
Die Punkte \(D\), \(E\) und \(F\) liegen in der Ebene \(L\).

Ermitteln Sie eine Gleichung von \(L\) in Koordinatenform.

(zur Kontrolle: \(2x_1 + 4x_2 + 3x_3 - 42 = 0\))

(4 BE) 

Gegeben sind in einem kartesischen Koordinatensystem die Ebene \(E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0\) und die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}, \; \lambda \in \mathbb R\,.\)

Erläutern Sie, warum die folgende Rechnung ein Nachweis dafür ist, dass \(g\) und \(E\) genau einen gemeinsamen Punkt haben:

\[\begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix} = -72 \neq 0\]

(1 BE)

Ermitteln Sie eine Gleichung der Ebene \(E\) in Normalenform.

(mögliches Ergebnis: \(E \colon 3x_{1} - x_{2} + 5x_{3} - 5 = 0\))

(3 BE)