Unabhängigkeit von Ereignissen
Zwei Ereignisse \(A\) und \(B\) werden als stochastisch unabhängig bezeichnet, wenn das Eintreten des Ereignisses \(A\) keinen Einfluss auf das Eintreten des Ereignisses \(B\) hat und umgekehrt das Eintreten des Ereignisses \(B\) keinen Einfluss auf das Eintreten des Ereignisses \(A\) hat. Das heißt, wenn \(P_{A}(B) = P(B)\) und \(P_{B}(A) = P(A)\) gilt.
Mit \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)}\) und \(P_{B}(A) = \dfrac{P(A \cap B)}{P(B)}\) ergibt sich (vgl. Abiturskript - 3.1.5 Bedingte Wahrscheinlichkeit):
\[P(B) = \frac{P(A \cap B)}{P(A)} \quad \Longleftrightarrow \quad P(A) \cdot P(B) = P(A \cap B)\]
bzw.
\[P(A) = \frac{P(A \cap B)}{P(B)} \quad \Longleftrightarrow \quad P(A) \cdot P(B) = P(A \cap B)\]
Stochastische Unabhängigkeit
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B) \;\) gilt. (vgl. Merkhilfe)
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Die Unabhängigkeit zweier Ereignisse \(A\) und \(B\) darf nicht mit der Unvereinbarkeit zweier Ereignisse \(A\) und \(B\) verwechselt werden. Im Falle der Unvereinbarkeit gilt \(A \cap B = \{\,\}\) und folglich \(P(A \cap B) = P(\{\,\}) = 0\).
Baumdiagramm zweier unabhängiger Ereignisse
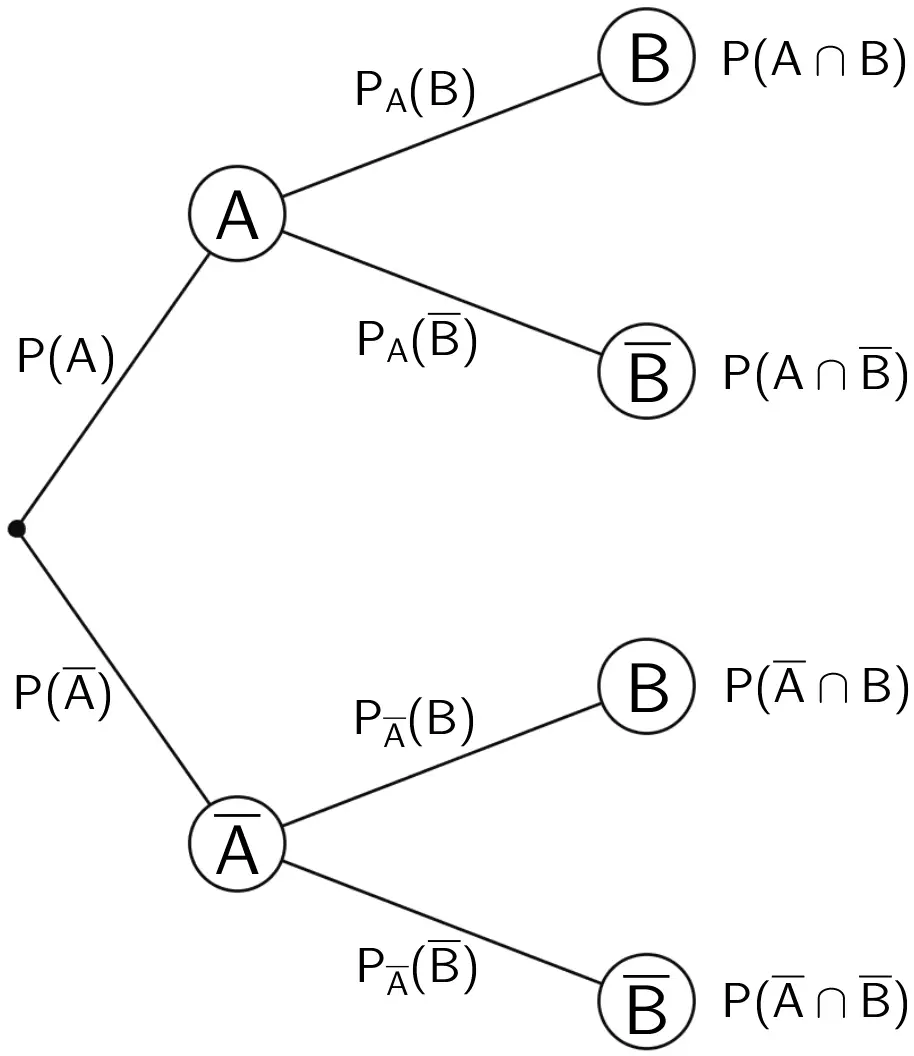
Stochastisch abhängige Ereignisse \(A\) und \(B\)
An den Pfaden der zweiten Stufe stehen die bedingten Wahrscheinlichkeiten.
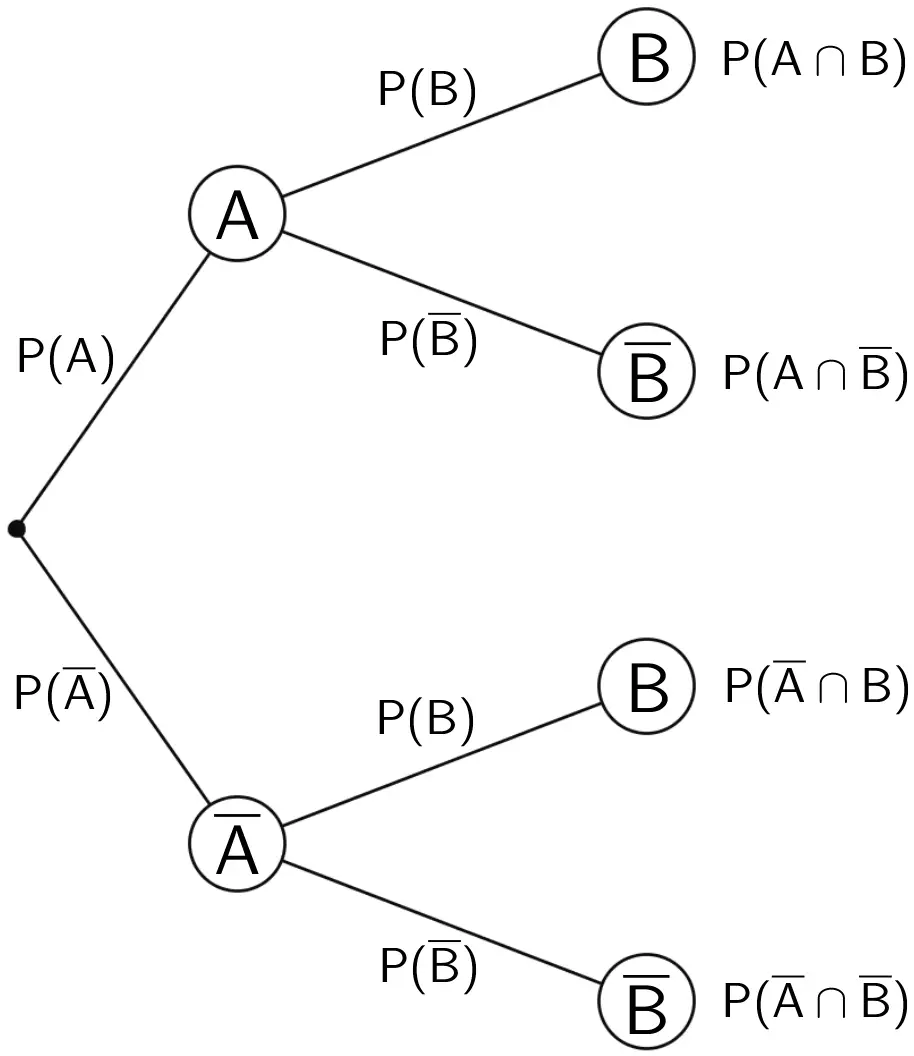
Stochastisch unabhängige Ereignisse \(A\) und \(B\)
An den Pfaden der zweiten Stufe stehen die Wahrscheinlichkeiten der unabhängigen Ereignisse.
Vierfeldertafel zweier unabhängiger Ereignisse
Im Falle zweier stochastisch unabhängiger Ereignisse \(A\) und \(B\) ist die Vierfeldertafel der Wahrscheinlichkeiten eine Multiplikationstafel. Das bedeutet, dass die Einträge der inneren Zellen das Produkt der Einträge der zugehörigen Randzellen sind.
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(P(A \cap B) = P(A) \cdot P(B)\) | \(P(\overline{A} \cap B) = P(\overline{A}) \cdot P(B)\) | \(P(B)\) |
| \(\overline{B}\) | \(P(A \cap \overline{B}) = P(A) \cdot P(\overline{B})\) | \(P(\overline{A} \cap \overline{B}) = P(\overline{A}) \cdot P(\overline{B})\) | \(P(\overline{B})\) |
| \(P(A)\) | \(P(\overline{A})\) | \(1\) |
Vierfeldertafel der Wahrscheinlichkeiten zweier stochastisch unabhängiger Ereignisse \(A\) und \(B\)
Anhand der Vierfeldertafel wird deutlich, dass sich die stochastische Unabhängigkeit zweier Ereignisse \(A\) und \(B\) wahlweise durch die Gültigkeit einer der Gleichungen
\(P(A \cap B) = P(A) \cdot P(B)\) oder
\(P(\overline{A} \cap B) = P(\overline{A}) \cdot P(B)\) oder
\(P(A \cap \overline{B}) = P(A) \cdot P(\overline{B})\) oder
\(P(\overline{A} \cap \overline{B}) = P(\overline{A}) \cdot P(\overline{B})\) nachweisen lässt.
Beispielaufgabe
Bei der Herstellung eines Smartphone Akkus eines bestimmten Typs entstehen zwei Arten von Fehlern. 2 % der Akkus entladen sich im Standby Betrieb zu schnell. Bei 5 % der Akkus weist das Gehäuse einen Formfehler auf. 99,9 % der Akkus sind fehlerfrei oder zeigen nur einen der beiden Fehler.
Überprüfen Sie die Ereignisse
\(E\): „Ein zufällig ausgewählter Akku entlädt sich im Standby Betrieb zu schnell." und
\(F\): „Bei einem zufällig ausgewählten Akku weist das Gehäuse einen Formfehler auf."
auf stochastische Unabhängigkeit.
Gegeben:
\(P(E) =0{,}02\), \(P(F) = 0{,}05\), \(P(\overline{E} \cup \overline{F}) = 0{,}999\)
Mit den gegebenen Wahrscheinlichkeiten lässt sich die stochastische Unabhängigkeit der Ereignisse \(E\) und \(F\) nicht auf Anhieb überprüfen. Nachfolgen werden zwei mögliche Vorgehensweisen vorgestellt.
1. Möglichkeit: \(P(E) \cdot P(F) = P(E \cap F)\) überprüfen
Die Wahrscheinlichkeit des Ereignisses \(E \cap F\) kann mithilfe des Gesetzes von De Morgan \(\overline{A} \cup \overline{B} = \overline{A \cap B}\) ermittelt werden (vgl. Abiturskript - 3.1.1 Ereignisse, Gesetze der Ereignisalgebra).
\[\overline{E} \cup \overline{F} = \overline{E \cap F} = \Omega \backslash (E \cap F)\]
\[\begin{align*}\Longrightarrow \quad P(\overline{E} \cup \overline{F}) &= 1 - P(E \cap F) \\[0.8em] \Longleftrightarrow \quad P(E \cap F) &= 1 - P(\overline{E} \cup \overline{F}) \\[0.8em] &= 1 - 0{,}999 \\[0.8em] &= 0{,}001\end{align*}\]
\[P(E) \cdot P(F) = 0{,}02 \cdot 0{,}05 = 0{,}001\]
\[\Longrightarrow P(E) \cdot P(F) = P(E \cap F)\]
\(\Longrightarrow \quad\)Die Ereignisse \(E\) und \(F\) sind stochastisch unabhängig.
2. Möglichkeit: \(P(\overline{E}) \cdot P(\overline{F}) = P(\overline{E} \cap \overline{F})\) überprüfen
\[P(\overline{E}) = 1 - P(E) = 1 - 0{,}02 = 0{,}98\]
\[P(\overline{F}) = 1 - P(F) = 1 - 0{,}05 = 0{,}95\]
Die Wahrscheinlichkeit des Ereignisses \(\overline{E} \cap \overline{F}\) lässt sich mithilfe des Additionssatzes berechnen (vgl. Abiturskript - 3.1.2 Wahrscheinlichkeitsbegriff, Eigenschaften der Wahrscheinlichkeiten).
\[\begin{align*}P(\overline{E} \cup \overline{F}) &= P(\overline{E}) + P(\overline{F}) - P(\overline{E} \cap \overline{F}) \\[0.8em] \Longleftrightarrow \quad P(\overline{E} \cap \overline{F}) &= P(\overline{E}) + P(\overline{F}) - P(\overline{E} \cup \overline{F}) \\[0.8em] &= 0{,}98 + 0{,}95 - 0{,}999 \\[0.8em] &= 0{,}931 \end{align*}\]
\[P(\overline{E}) \cdot P(\overline{F}) = 0{,}98 \cdot 0{,}95 = 0{,}931\]
\[\Longrightarrow P(\overline{E}) \cdot P(\overline{F}) = P(\overline{E} \cap \overline{F})\]
\(\Longrightarrow \quad\)Die Ereignisse \(E\) und \(F\) sind stochastisch unabhängig.

