Signifikanztest
Ein Signifikanztest für eine unbekannte Wahrscheinlichkeit \(p\) ist ein Hypothesentest, welcher der Wahrscheinlichkeit für den Fehler 1. Art eine Obergrenze, das sog. Signivikanzniveau \(\boldsymbol{\alpha}\), vorgibt. Da die Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art vom Ablehnungsbereich \(\overline{A}\) der Nullhypothese \(H_{0}\) abhängt (vgl. Abiturskript - 3.4.1 Hypothesentest, Fehler 1. Art), liefert ein Signifikanztest durch die Vorgabe des Signifikanzniveaus \(\alpha\) den Ablehnungsbereich der Nullhypothese und somit die Entscheidungsregel für den Test.
Die Nullhypothese \(H_{0}\) wird bei einem Signifikanztest in der Regel so formuliert, dass ein im Sachzusammenhang als schwerwiegend erachteter Fehler durch den Fehler 1. Art (\(H_{0}\) wird irrtümlich abgelehnt) beschrieben wird und somit durch das Signifikanzniveau \(\alpha\) begrenzt wird.
Einseitiger Signifikanztest
Ein einseitiger Signifikanztest zum Signifikanzniveau \(\boldsymbol{\alpha}\) überprüft eine Vermutung (z.B. auf der Grundlage neuer Erkenntnisse), dass eine Wahrscheinlichkeit \(p\) größer bzw. kleiner als eine bestimmte Wahrscheinlichkeit \(p_{0}\) ist. Meistens vertritt die Gegenhypothese \(H_{1}\) die Vermutung, welche nur angenommen werden soll, wenn die Wahrscheinlichkeit \(\alpha'\) für den Fehler 1. Art höchstens den Wert des Signifikanzniveaus \(\alpha\) erreicht.
Anmerkung:
Bei einem Signifikanztest betrachtet man im Falle einer Nullhypothese \(H_{0} \colon p \leq p_{0}\) oder \(H_{0} \colon p \geq p_{0}\) den „Extremfall" \(p = p_{0}\), um den Annahme- und Ablehnungsbereich der Nullhypothese zu bestimmen. Damit ist gewährleistet, dass die Wahrscheinlichkeit für den Fehler 1. Art auch für \(p < p_{0}\) bzw. \(p > p_{0}\) nicht das Signifikanzniveau \(\alpha\) überschreitet.
Linksseitiger Signifikanztest
Beim linksseitigen Signifikanztest liegt der Ablehnungsbereich \(\overline{A}\) der Nullhypothese \(H_{0}\) links vom Erwartungswert \(\mu\) der nach \(B(n;p)\) binomialverteilten Testgröße \(X\) (Zufallsgröße).
\(H_{0} \colon p \geq p_{0} \qquad H_{1} \colon p < p_{0}\)
\(\overline{A} = \{0, 1, \dots, k\} \qquad A = \{k + 1, \dots, n\}\)
Bedingung für den Fehler 1. Art formulieren:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\leq \alpha \end{align*}\]
Stochastisches Tafelwerk (ST) verwenden:
Bei bekannter Trefferwahrscheinlichkeit \(p_{0}\) und bekannter Länge der Bernoulli-Kette \(n\) wählt man in der rechten Spalte (kumulative Verteilungsfunktion) der entsprechenden Tabelle diejenige Anzahl \(k\), welche die Bedingung \(P_{p_{0}}^{n}(X \leq k) \leq \alpha\) möglichst genau erfüllt.
\[P_{p_{0}}^{n}(X \leq k) \leq \alpha \quad \overset{\text{ST}}{\Longrightarrow} \quad k\]
Entscheidungsregel formulieren:
\[k \quad \Longrightarrow \quad A, \overline{A}\]
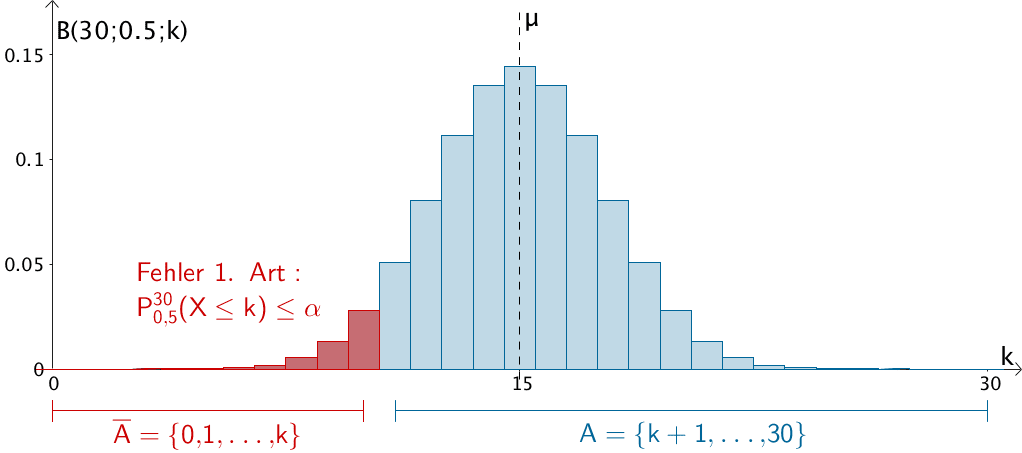
Beispiel: Linksseitiger Signifikanztest der Nullhypothese \(H_{0}\colon p \geq 0{,}5\) zum Signifikanzniveau \(\alpha\) bei einem Stichprobenumfang von \(n = 30\)
Rechtsseitiger Signifikanztest
Beim rechtsseitigen Signifikanztest liegt der Ablehnungsbereich \(\overline{A}\) der Nullhypothese \(H_{0}\) rechts vom Erwartungswert \(\mu\) der nach \(B(n;p)\) binomialverteilten Testgröße \(X\) (Zufallsgröße).
\(H_{0} \colon p \leq p_{0} \qquad H_{1} \colon p > p_{0}\)
\(A = \{0, 1, \dots, k\} \qquad \overline{A} = \{k + 1, \dots, n\}\)
Bedingung für den Fehler 1. Art formulieren:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \geq k +1) &\leq \alpha & &| \;\text{Gegenereignis betrachten} \\[0.8em] 1 - P_{p_{0}}^{n}(X \leq k) &\leq \alpha & &| - 1 \\[0.8em] - P_{p_{0}}^{n}(X \leq k) &\leq \alpha - 1 & &| \cdot (-1) \enspace \textcolor{red}{\text{Relationszeichen dreht!}} \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\textcolor{red}{\geq} 1 - \alpha \end{align*}\]
Stochastisches Tafelwerk (ST) verwenden:
Bei bekannter Trefferwahrscheinlichkeit \(p_{0}\) und bekannter Länge der Bernoulli-Kette \(n\) wählt man in der rechten Spalte (kumulative Verteilungsfunktion) der entsprechenden Tabelle diejenige Anzahl \(k\), welche die Bedingung \(P_{p_{0}}^{n}(X \leq k) \geq 1 - \alpha\) möglichst genau erfüllt.
\[P_{p_{0}}^{n}(X \leq k) \geq 1 - \alpha \quad \overset{\text{ST}}{\Longrightarrow} \quad k\]
Entscheidungsregel formulieren:
\[k \quad \Longrightarrow \quad A, \overline{A}\]
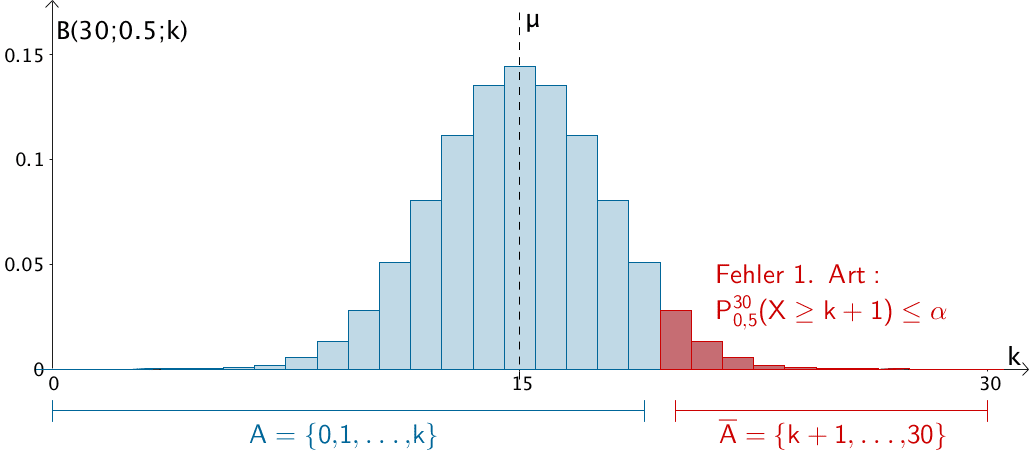
Beispiel: Rechtsseitiger Signifikanztest der Nullhypothese \(H_{0}\colon p \leq 0{,}5\) zum Signifikanzniveau \(\alpha\) bei einem Stichprobenumfang von \(n = 30\)
Anmerkung:
Für die Bearbeitung einer Aufgabe zum Thema „Einseitiger Signifikanztest" ist die Unterscheidung nach linksseitigem und rechtsseitigem Signifikanztest nicht zwingend erforderlich. Entscheidend ist die Bedeutung der Zufallsgröße \(X\) (Testgröße) sowie die Festlegung der Nullhypothese und des Ablehnungsbereichs der Nullhypothese. Wie die Nullhypothese lautet, ergibt sich aus der Aufgabenstellung. Die Art der Nullhypothese lässt auf den Ablehnungsbereich der Nullhypothese schließen.
Festlegen des Ablehnungsbereichs der Nullhypothese
Bei einem Stichprobenumfang \(n\) kann eine Zufallsgröße \(X\) (Testgröße) die (ganzzahligen) Werte \(x_{i} \in \{0,1, \dots, n\}\) annehmen (mögliche Stichprobenergebnisse, mögliche Trefferanzahlen). Die Teilbereiche \(\{0,1,\dots,k\}\) und \(\{k+1, \dots,n\}\) bilden den Definitionsbereich der Zufallsgröße \(X\) vollständig ab. Welcher dieser Teilbereiche der Annahmebereich bzw. der Ablehnungsbereich der Nullhypothese ist, sowie die Lage der Bereichsgrenzen \(k\) bzw. \(k + 1\), hängt davon ab, wie die Nullhypothese lautet.
Der Ablehnungsbereich einer Nullhypothese lässt sich beispielsweise wie folgt bestimmen:
Lautet die Nullhypothese \(H_{0}\colon p \geq p_{0}\) („mindestens \(p_{0}\)"), schließt diese den theoretischen Grenzfall \(p_{0} = 1\) mit ein. Ein Ereignis, das mit der Trefferwahrscheinlichkeit \(p_{0} = 1\) eintritt, wird durch \(n\) Treffer bestätigt. Folglich liegt die Trefferanzahl \(n\) im Annahmebereich der Nullhypothese. Der Annahmebereich der Nullhypothese ergibt sich somit zu \(A = \{k + 1, \dots, n\}\) und der Ablehnungsbereich der Nullhypothese zu \(\overline{A} = \{0,1, \dots, k\}\).
Lautet die Nullhypothese \(H_{0}\colon p \leq p_{0}\) („höchstens \(p_{0}\)"), schließt diese den theoretischen Grenzfall \(p_{0} = 0\) mit ein. Ein Ereignis, das mit der Trefferwahrscheinlichkeit \(p_{0} = 0\) eintritt, wird durch \(0\) Treffer bestätigt. Folglich liegt die Trefferanzahl \(0\) im Annahmebereich der Nullhypothese. Der Annahmebereich der Nullhypothese ergibt sich somit zu \(A = \{0,1, \dots, k\}\) und der Ablehnungsbereich der Nullhypothese zu \(\overline{A} = \{k + 1, \dots, n\}\).
Lautet die Nullhypothese \(H_{0}\colon p = p_{0}\), lässt der Sachzusammenhang darauf schließen, ob die Gegenhypothese \(H_{1}\colon p < p_{0}\) oder \(H_{1}\colon p > p_{0}\) lautet. Die Gegenhypothesen schließen die theoretischen Grenzfälle \(p_{1} = 0\) bzw. \(p_{1} = 1\) ein. Daraus ergibt sich der Annahmebereich der Gegenhypothese, der zugleich der Ablehnungsbereich der Nullhypothese ist.
Ist der Ablehnungsbereich der Nullhypothese festgelegt, erfolgt der Ansatz \(P_{p_{0}}^{n}(X \in \overline{A}) \leq \alpha\), welcher ggf. die Rückführung auf die kumulative Verteilungsfunktion \(P_{p_{0}}^{n}(X \leq k)\) erforderlich macht (vgl. Rechtsseitiger Signifikanztest).
Beispielaufgaben
Die nachfolgenden Aufgabenvariationen sollen verdeutlichen, dass der Schwierigkeitsgrad einer Aufgabe zum Thema Signifikanztest wesentlich von der Festlegung der Nullhypothese abhängt. Im einfachsten Fall nennt die Aufgabenstellung die Nullhypothese. Etwas schwieriger sind Aufgaben, bei denen die Nullhypothese aus dem Kontext zu formulieren ist oder eine geeignete Nullhypothese gewählt werden soll.
1. Beispielaufgabe
Ein Schreibwarenhändler bezieht von seinem Lieferanten regelmäßig Textmarker einer bestimmten Marke. Im Folgenden werden nur Textmarker dieser Marke betrachtet.
In jüngster Zeit häufen sich die Reklamationen der Kunden, die Textmarker seien bereits ab dem Kaufdatum eingetrocknet. Der Schreibwarenhändler vermutet, dass deshalb mindestens jeder fünfte verkaufte Textmarker zu einer Reklamation führt und überlegt, die Textmarker aus seinem Angebotssortiment zu nehmen. Auf die Reklamationen angesprochen, beteuert der Lieferant die hochwertige Qualität der Textmarker und mutmaßt eine unsachgemäße Handhabung als Grund für die Reklamationen. Der Schreibwarenhändler und der Lieferant beschließen die nächste Lieferung anhand einer Stichprobe von 100 Textmarkern auf dem Signifikanzniveau 5 % zu testen. Sie einigen sich auf die Nullhypothese \(H_{0} \colon p \geq 0{,}2\), „Mindestens 20 % der Textmarker rechtfertigen eine Reklamation."
a) Welche Absicht vertritt die Nullhypothese „Mindestens 20 % der Textmarker rechtfertigen eine Reklamation."?
b) Bestimmen Sie die zugehörige Entscheidungsregel.
a) Begründung der Wahl der Nullhypothese
Mit der Wahl der Nullhypothese „Mindestens 20 % der Textmarker rechtfertigen eine Reklamation." soll die Wahrscheinlichkeit dafür, dass tatsächlich mindestens 20 % der Textmarker eingetrocknet sind, dies aber nicht erkannt wird, weil das zufällige Ergebnis der Stichprobe nur wenige eingetrocknete Textmarker liefert, höchstens 5 % betragen (Wahrscheinlichkeit für den Fehler 1. Art).
Die Nullhypothese vertritt damit das Interesse des Schreibwarenhändlers, der nicht irrtümlich Textmarker von minderer Qualität einkaufen möchte.
b) Bestimmung der Entscheidungsregel
Zufallsgröße \(X\) (Testgröße) beschreiben:
Bei einem Stichprobenumfang von 100 Textmarkern wird das Ereignis „Textmarker ist eingetrocknet" betrachtet. Die Wahrscheinlichkeit für dieses Ereignis ist gemäß der Nullhypothese mit \(p_{0}\) konstant.
Zufallsgröße \(X\): Anzahl der eingetrockneten Textmarker
Die Zufallsgröße \(X\) ist nach \(B(100;p_{0})\) binomialverteilt.
Nullhypothese (und Gegenhypothese) festlegen:
In diesem Fall ist die Nullhypothese vorgegeben. Die Gegenhypothese ergibt sich daraus.
\[H_{0} \colon p \geq 0{,}2 \qquad H_{1} \colon p < 0{,}2\]
(Annahme- und) Ablehnungsbereich der Nullhypothese formulieren:
Die Nullhypothese „Mindestens 20 % der Textmarker rechtfertigen eine Reklamation" schließt den theoretischen Grenzfall „100 % der Textmarker rechtfertigen eine Reklamation" mit ein. Dieser wird bestätigt, wenn alle 100 getesteten Textmarker eingetrocknet sind. Folglich liegt das Stichprobenergebnis \(n = 100\) im Annahmebereich der Nullhypothese. Die Nullhypothese wird also abgelehnt, wenn das Ergebnis der Stichprobe „tendenziell wenige" \((\{0,1,\dots,k\})\) eingetrocknete Textmarker liefert.
\[\overline{A} = \{0, 1, \dots, k\} \qquad A = \{k + 1, \dots, 100\}\]
Bedingung für den Fehler 1. Art formulieren:
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Signifikanzniveau: \(\alpha = 0{,}05\)
Im Falle der Nullhypothese \(H_{0}\colon p \geq 0{,}2\) genügt es, den „Extremfall" \(p_{0} = 0{,}2\) zu betrachten.
\[\begin{align*}P_{p_{0}}^{n}(\text{Fehler 1. Art}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{0{,}2}^{100}(X \leq k) &\leq 0{,}05 \end{align*}\]
Stochastisches Tafelwerk (ST) verwenden:
\[\begin{align*} P_{0{,}2}^{100}(X \leq k) &\leq 0{,}05 \\[0.8em] \sum \limits_{i = 0}^{k}B(100;0{,}2;i) &\leq 0{,}05 \end{align*}\]
Der Wert der kumulativen Verteilungsfunktion \(\sum \limits_{i = 0}^{k}B(100;0{,}2;i)\) darf höchstens den Wert \(0{,}05\) annehmen. Unter Verwendung des Stochastischen Takelwerks ergibt sich für \(p = 0{,}2\) und \(n = 100\) in der rechten Spalte des Tafelwerks der Wert \(0{,}04691\) für \(k = 13\).
\[\sum \limits_{i = 0}^{k}B(100;0{,}2;i) \leq 0{,}05 \quad \overset{\text{ST}}{\Longrightarrow} \quad k = 13\]
\[\left( P_{0{,}2}^{100}(X \leq 13) = \sum \limits_{i = 0}^{13}B(100;0{,}2;i) = 0{,}04691\right)\]
Zum Vergleich:
\[k = 14 \quad \overset{\text{ST}}{\Longrightarrow} \quad \sum \limits_{i = 0}^{14}B(100;0{,}2;i) = 0{,}08044\]
Für \(k = 14\) liegt der Wert der kumulativen Verteilungsfunktion \(\sum \limits_{i = 0}^{k}B(100;0{,}2;i)\) mit \(0{,}08044\) bereits über dem Signifikanzniveau \(\alpha = 0{,}05\).
Entscheidungsregel formulieren:
Mit \(k = 13\) lässt sich der Annahme- und Ablehnungsbereich der Nullhypothese \(H_{0}\) konkretisieren.
\[\overline{A} = \{0, 1, \dots, 13\} \qquad A = \{14, \dots, 100\}\]
Wenn höchstens 13 Textmarker der 100 getesteten Textmarker eingetrocknet sind, wird die Vermutung „Mindestens 20 % der Textmarker rechtfertigen eine Reklamation." verworfen.
oder:
Wenn mindestens 14 Textmarker der 100 getesteten Textmarker eingetrocknet sind, wird die Vermutung „Mindestens 20 % der Textmarker rechtfertigen eine Reklamation." bestätigt.
Die Wahrscheinlichkeit dafür, dass der Schreibwarenhändler irrtümlich Textmarker minderer Qualität einkauft (Fehler 1. Art), beträgt dabei höchstens:
\[P_{0{,}2}^{100}(X \leq 13) = \sum \limits_{i = 0}^{13}B(100;0{,}2;i) = 0{,}04691 \approx 4{,}7\,\%\]
Das Signifikanzniveau 5 % (Obergrenze für die Wahrscheinlichkeit des Fehlers 1. Art) wird somit eingehalten.
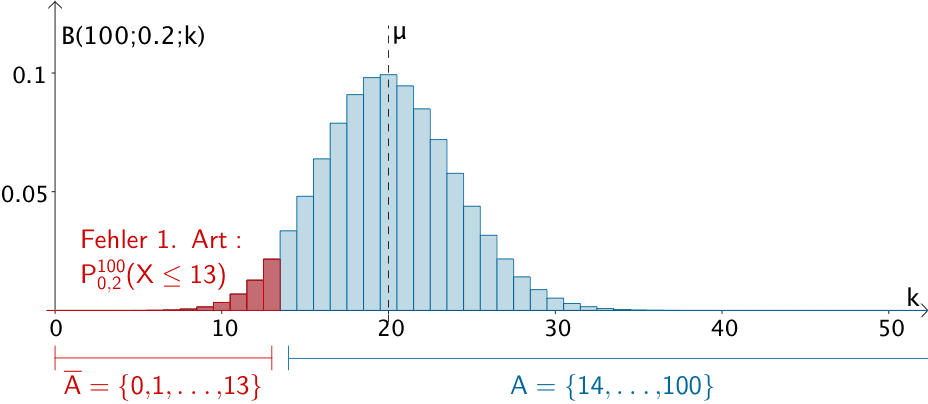
Linksseitiger Signifikanztest der Nullhypothese \(H_{0}\colon p \geq 0{,}2\) zum Signifikanzniveau \(\alpha = 5\,\%\) bei einem Stichprobenumfang von \(n = 100\) (verkürzte Darstellung bis \(k = 50\))
2. Beispielaufgabe
Ein Schreibwarenhändler bezieht von seinem Lieferanten regelmäßig Textmarker einer bestimmten Marke. Im Folgenden werden nur Textmarker dieser Marke betrachtet.
In jüngster Zeit häufen sich die Reklamationen der Kunden, die Textmarker seien bereits ab dem Kaufdatum eingetrocknet. Der Schreibwarenhändler vermutet, dass deshalb mindestens jeder fünfte verkaufte Textmarker zu einer Reklamation führt und überlegt, die Textmarker aus seinem Angebotssortiment zu nehmen. Auf die Reklamationen angesprochen, beteuert der Lieferant die hochwertige Qualität der Textmarker und mutmaßt eine unsachgemäße Handhabung als Grund für die Reklamationen. Der Schreibwarenhändler und der Lieferant beschließen die nächste Lieferung anhand einer Stichprobe von 100 Textmarkern zu testen. Die Wahrscheinlichkeit dafür, dass der Schreibwarenhändler die Textmarker irrtümlich aus seinem Angebotssortiment nimmt, soll höchstens 5 % betragen.
Bestimmen Sie die zugehörige Entscheidungsregel.
Zufallsgröße \(X\) (Testgröße) beschreiben:
Bei einem Stichprobenumfang von 100 Textmarkern wird das Ereignis „Textmarker ist eingetrocknet" betrachtet. Die Wahrscheinlichkeit für dieses Ereignis ist gemäß der Nullhypothese mit \(p_{0}\) konstant.
Zufallsgröße \(X\): Anzahl der eingetrockneten Textmarker
Die Zufallsgröße \(X\) ist nach \(B(100;p_{0})\) binomialverteilt.
Nullhypothese (und Gegenhypothese) festlegen:
In diesem Fall muss die Nullhypothese aus dem Kontext heraus formuliert werden. Ein Signifikanztest bedeutet per Definition, dass die Wahrscheinlichkeit für den Fehler 1. Art höchstens das Signifikanzniveau erreichen darf. Der Fehler 1. Art wiederum nimmt Bezug auf die Nullhypothese. Formuliert die Angabe eine Wahrscheinlichkeit für einen im Sinne eines Signifikanztests zu begrenzenden Fehler (Irrtumswahrscheinlichkeit), ist dieser Fehler als Fehler 1. Art zu betrachten und damit ein Hinweis auf die Nullhypothese.
Bei der vorliegenden Aufgabe heißt es: „Die Wahrscheinlichkeit dafür, dass der Schreibwarenhändler die Textmarker irrtümlich aus seinem Angebotssortiment nimmt, soll höchstens 5 % betragen." Dieser Sachverhalt beschreibt die Wahrscheinlichkeit für den zu begrenzenden Fehler 1. Art (Signifikanztest). Der Schreibwarenhändler nimmt die Textmarker dann irrtümlich aus dem Angebotssortiment, wenn die Wahrscheinlichkeit dafür, dass ein Textmarker eingetrocknet ist, in Wirklichkeit höchstens bei 20 % liegt, dies aber nicht erkannt wird, weil das zufällige Ergebnis der Stichprobe viele eingetrocknete Textmarker liefert. Folglich lautet die Nullhypothese \(H_{0}\): „Höchstens 20 % der Textmarker rechtfertigen eine Reklamation."
Diese Nullhypothese vertritt das Interesse des Lieferanten, der vermeiden möchte, dass der Schreibwarenhändler den Einkauf der Textmarker einstellt, obwohl diese von gewohnt guter Qualität sind.
\[H_{0} \colon p \leq 0{,}2 \qquad H_{1} \colon p > 0{,}2\]
(Annahme- und) Ablehnungsbereich der Nullhypothese formulieren:
Die Nullhypothese „Höchstens 20 % der Textmarker rechtfertigen eine Reklamation" schließt den theoretischen Grenzfall „0 % der Textmarker rechtfertigen eine Reklamation" mit ein. Dieser wird bestätigt, wenn keiner der getesteten Textmarker eingetrocknet ist. Folglich liegt das Stichprobenergebnis \(x_{1} = 0\) im Annahmebereich der Nullhypothese. Die Nullhypothese wird also abgelehnt, wenn das Ergebnis der Stichprobe „tendenziell viele" \((\{k+ 1, \dots,100\})\) eingetrocknete Textmarker liefert.
\[A = \{0, 1, \dots, k\} \qquad \overline{A} = \{k + 1, \dots, 100\}\]
Bedingung für den Fehler 1. Art formulieren:
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Signifikanzniveau: \(\alpha = 0{,}05\)
Im Falle der Nullhypothese \(H_{0}\colon p \leq 0{,}2\) genügt es, den „Extremfall" \(p_{0} = 0{,}2\) zu betrachten.
\[\begin{align*}P_{p_{0}}^{n}(\text{Fehler 1. Art}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{0{,}2}^{100}(X \geq k + 1) &\leq 0{,}05 & &| \;\text{Gegenereignis betrachtetn} \\[0.8em] 1 - P_{0{,}2}^{100}(X \leq k) &\leq 0{,}05 & &| - 1 \\[0.8em] -P_{0{,}2}^{100}(X \leq k) &\leq -0{,}95 & &| \cdot (-1) \enspace \text{Relationszeichen dreht!} \\[0.8em] P_{0{,}2}^{100}(X \leq k) &\geq 0{,}95 \end{align*}\]
Stochastisches Tafelwerk (ST) verwenden:
\[\begin{align*} P_{0{,}2}^{100}(X \leq k) &\geq 0{,}95 \\[0.8em] \sum \limits_{i = 0}^{k}B(100;0{,}2;i) &\geq 0{,}95 \end{align*}\]
Der Wert der kumulativen Verteilungsfunktion \(\sum \limits_{i = 0}^{k}B(100;0{,}2;i)\) muss mindestens den Wert \(0{,}95\) annehmen. Unter Verwendung des Stochastischen Takelwerks ergibt sich für \(p = 0{,}2\) und \(n = 100\) in der rechten Spalte des Tafelwerks der Wert \(0{,}96585\) für \(k = 27\).
\[\sum \limits_{i = 0}^{k}B(100;0{,}2;i) \geq 0{,}95 \quad \overset{\text{ST}}{\Longrightarrow} \quad k = 27\]
\[\left( P_{0{,}2}^{100}(X \leq 27) = \sum \limits_{i = 0}^{27}B(100;0{,}2;i) = 0{,}96585 \right)\]
Zum Vergleich:
\[k = 26 \quad \overset{\text{ST}}{\Longrightarrow} \quad \sum \limits_{i = 0}^{26}B(100;0{,}2;i) = 0{,}94417\]
Für \(k = 26\) liegt der Wert der kumulativen Verteilungsfunktion \(\sum \limits_{i = 0}^{k}B(100;0{,}2;i)\) mit \(0{,}94417\) noch unter dem Wert \(0{,}95\).
Entscheidungsregel formulieren:
Mit \(k = 27\) lässt sich der Annahme- und Ablehnungsbereich der Nullhypothese \(H_{0}\) konkretisieren.
\[A = \{0, 1, \dots, 27\} \qquad \overline{A} = \{28, \dots, 100\}\]
Wenn höchstens 27 Textmarker der 100 getesteten Textmarker eingetrocknet sind, wird die Vermutung „Höchstens 20 % der Textmarker rechtfertigen eine Reklamation." bestätigt.
oder:
Wenn mindestens 28 Textmarker der 100 getesteten Textmarker eingetrocknet sind, wird die Vermutung „Höchstens 20 % der Textmarker rechtfertigen eine Reklamation." verworfen.
Die Wahrscheinlichkeit dafür, dass der Schreibwarenhändler die Textmarker irrtümlich aus dem Angebotssortiment nimmt (Fehler 1. Art), beträgt dabei höchstens:
\[\begin{align*}P_{0{,}2}^{100}(X \geq 28) &= 1 - P_{0{,}2}^{100}(X \leq 27) \\[0.8em] &= 1- \sum \limits_{i = 0}^{27}B(100;0{,}2;i) \\[0.8em] &\overset{\text{ST}}{=} 1- 0{,}96585 \\[0.8em] &= 0{,}03415 \\[0.8em] &\approx 3{,}4\,\%\end{align*}\]
Das Signifikanzniveau 5 % (Obergrenze für die Wahrscheinlichkeit des Fehlers 1. Art) wird somit eingehalten.
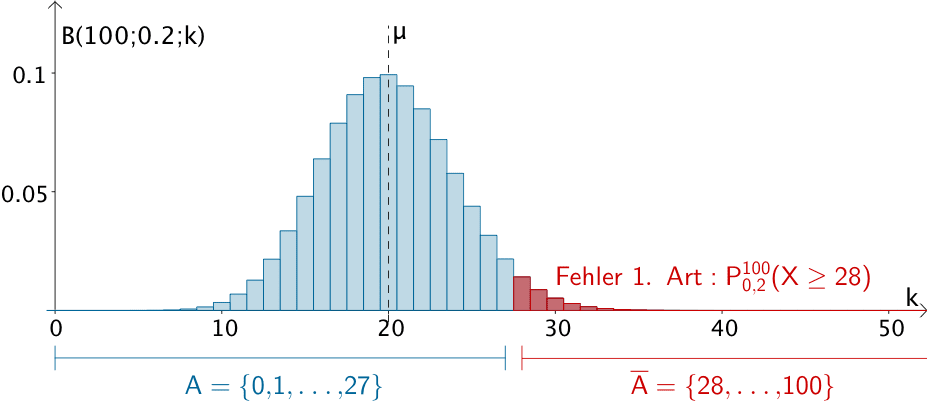
Rechtsseitiger Signifikanztest der Nullhypothese \(H_{0}\colon p \leq 0{,}2\) zum Signifikanzniveau \(\alpha = 5\,\%\) bei einem Stichprobenumfang von \(n = 100\) (verkürzte Darstellung bis \(k = 50\))
3. Beispielaufgabe
Ein Schreibwarenhändler bezieht von seinem Lieferanten regelmäßig Textmarker einer bestimmten Marke. Im Folgenden werden nur Textmarker dieser Marke betrachtet.
In jüngster Zeit häufen sich die Reklamationen der Kunden, die Textmarker seien bereits ab dem Kaufdatum eingetrocknet. Der Schreibwarenhändler vermutet, dass deshalb mindestens jeder fünfte verkaufte Textmarker zu einer Reklamation führt und überlegt, die Textmarker aus seinem Angebotssortiment zu nehmen. Auf die Reklamationen angesprochen, beteuert der Lieferant die hochwertige Qualität der Textmarker und mutmaßt eine unsachgemäße Handhabung als Grund für die Reklamationen. Der Schreibwarenhändler und der Lieferant beschließen die nächste Lieferung anhand einer Stichprobe von 100 Textmarkern auf dem Signifikanzniveau 5 % zu testen.
Wählen Sie eine im Sachzusammenhang sinnvolle Nullhypothese und bestimmen Sie die zugehörige Entscheidungsregel.
Wahl einer sinnvollen Nullhypothese
Das Signifikanzniveau ist eine Obergrenze für die Wahrscheinlichkeit des Fehlers 1. Art. Der Fehler 1. Art nimmt Bezug auf die Nullhypothese. Diese ist so zu wählen, dass deren irrtümliche Ablehnung einen im Sachzusammenhang schwerwiegenden Fehler 1. Art beschreibt (vgl. Abiturskript - 3.4.1 Hypothesentest, Fehler 1. Art). Ein möglicher schwerwiegender Fehler lässt sich sowohl aus der Sicht des Schreibwarenhändlers als auch aus der Sicht des Lieferanten beschreiben. Die Angabe „Der Schreibwarenhändler vermutet, dass deshalb mindestens jeder fünfte verkaufte Textmarker zu einer Reklamation führt ..." liefert eine Orientierung für die möglichen sinnvollen Nullhypothesen.
Interesse des Schreibwarenhändlers:
Der Schreibwarenhändler möchte den Fehler vermeiden, dass er irrtümlich weiterhin Textmarker minderer Qualität einkauft. Dieser Fehler tritt dann ein, wenn in Wirklichkeit mindestens 20 % der Textmarker eine Reklamation rechtfertigen, das zufällige Ergebnis der Stichprobe jedoch nur wenige eingetrocknete Textmarker liefert. Folglich wählt man die Nullhypothese „Mindestens 20 % der Textmarker rechtfertigen eine Reklamation.", um mit dem Signifikanztest das Interesse des Schreibwarenhändlers zu vertreten.
\(\Longrightarrow \quad\)Nullhypothese \(H_{0} \colon p \geq 0{,}2\)
Interesse des Lieferanten:
Der Lieferant möchte den Fehler vermeiden, dass der Schreibwarenhändler die Textmarker irrtümlich aus seinem Angebotssortiment nimmt. Dieser Fehler tritt dann ein, wenn in Wirklichkeit höchstens 20 % der Textmarker eine Reklamation rechtfertigen, das zufällige Ergebnis der Stichprobe jedoch viele eingetrocknete Textmarker liefert. Folglich wählt man die Nullhypothese „Höchstens 20 % der Textmarker rechtfertigen eine Reklamation.", um mit dem Signifikanztest das Interesse des Lieferanten zu vertreten.
\(\Longrightarrow \quad\)Nullhypothese \(H_{0} \colon p \leq 0{,}2\)
Bestimmung der zugehörigen Entscheidungsregel
Entscheidet man sich dafür, das Interesse des Schreibwarenhändlers vertreten zu wollen, testet man die Nullhypothese \(H_{0} \colon p \geq 0{,}2\) auf dem Signifikanzniveau 5 % (vgl. 1. Beispielaufgabe).
Entscheidet man sich dafür, das Interesse des Lieferanten vertreten zu wollen, testet man die Nullhypothese \(H_{0} \colon p \leq 0{,}2\) auf dem Signifikanzniveau 5 % (vgl. 2. Beispielaufgabe).

