Orthogonale Ebene zu einer Gerade
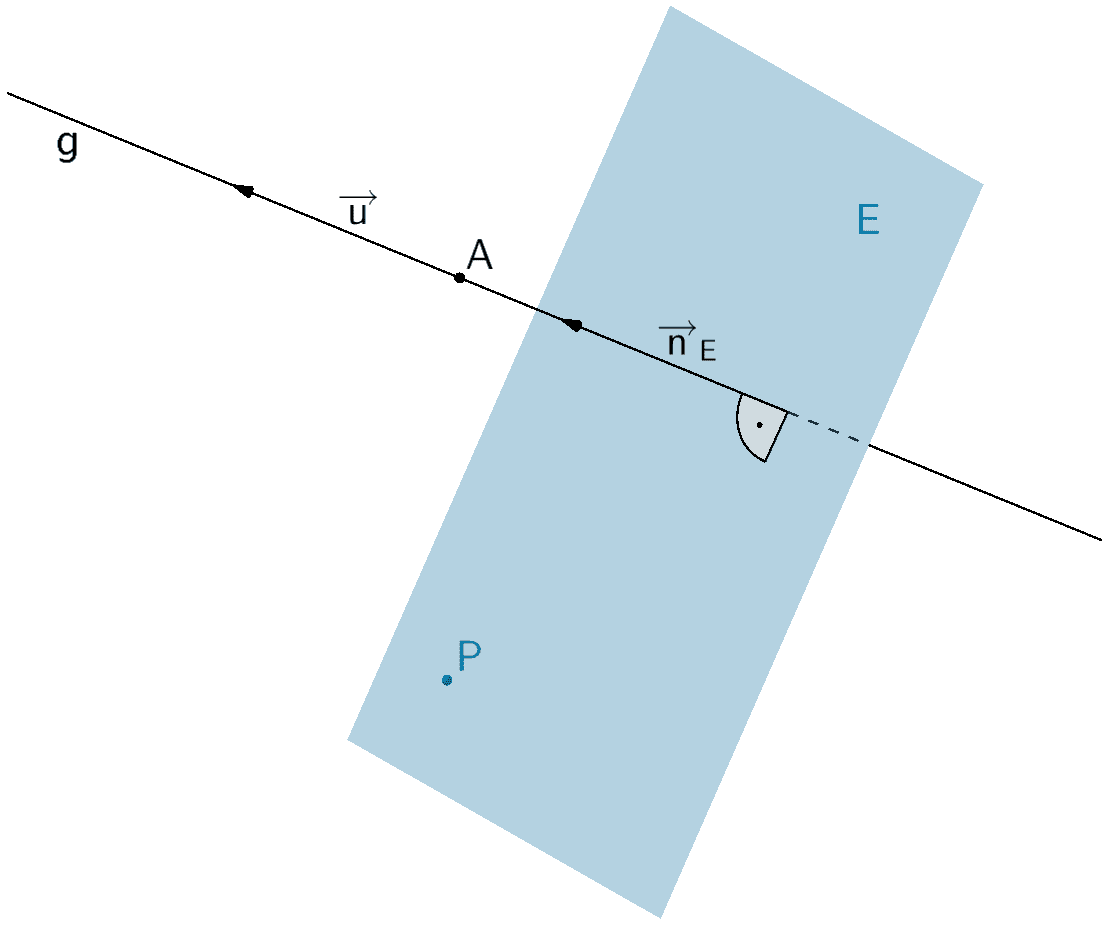
Eine orthogonale (senkrechte) Ebene \(E\) zu einer Gerade \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) ist durch einen beliebigen Punkt \(P \in E\) und den Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) eindeutig festgelegt.
\[E \colon \overrightarrow{u} \circ (\overrightarrow{X} - \overrightarrow{P})\]
Jedes Vielfache des Richtungsvektors \(\overrightarrow{u}\) der Gerade \(g\) ist ebenfalls ein Normalenvektor der Ebene \(E\).
Beispiel:
Gegeben sei die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\).
Geben Sie die Gleichung einer Ebene \(E\) an, welche den Punkt \(P(0|-4|3)\) enthält und senkrecht zur Gerade \(g\) ist.
\[g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix}\]
\[P(0|-4|3)\]
\[\Longrightarrow \quad E \colon \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix} \right] = 0\]

