Orthogonale Ebene zu einer Ebene

Nachfolgend werden zwei Fälle behandelt, welche eine orthogonale (senkrechte) Ebene \(F\) zu einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) festlegen. Zudem wird ein Fall einer zu zwei nicht parallelen Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B})\) orthogonalen Ebene \(G\) vorgestellt.

 

Orthogonale Ebene \(F\) durch zwei Punkte \(P\) und \(Q\) zu einer Ebene \(E\)

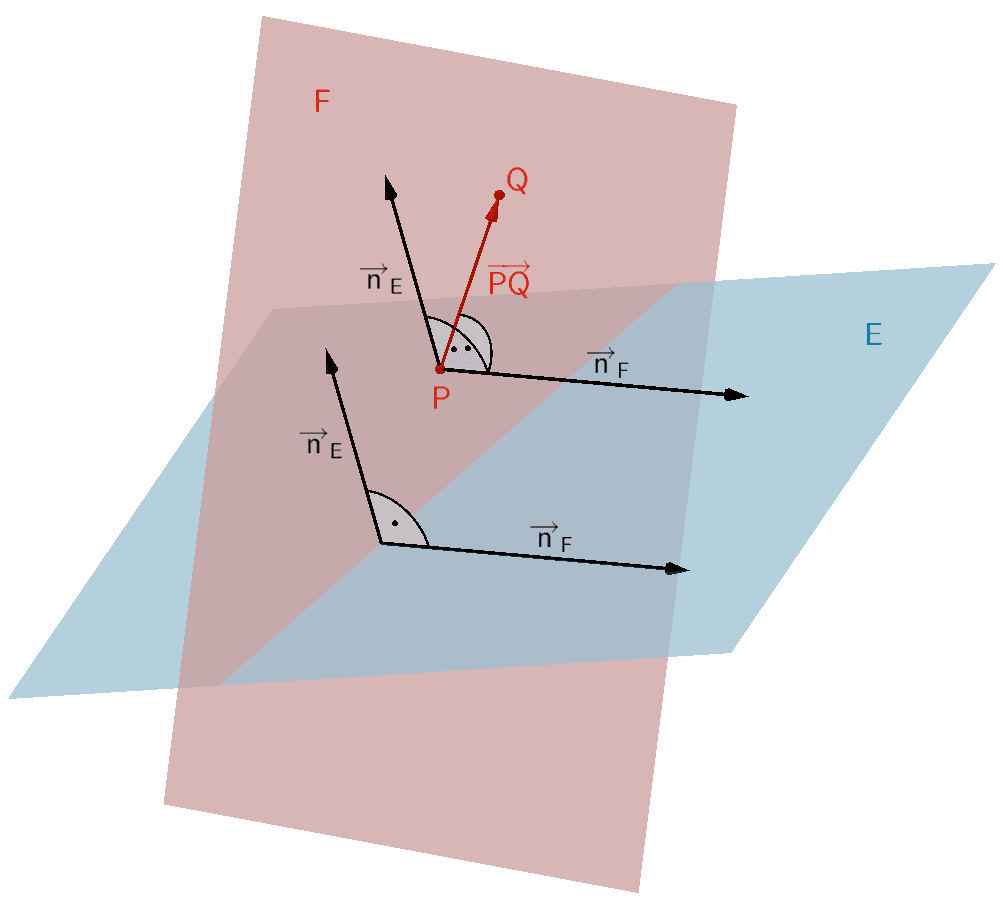
Eine orthogonale Ebene \(F\) zu einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) ist durch zwei Punkte \(P \in F\) und \(Q \in F\) \((P \neq Q)\) eindeutig festgelegt, wenn der Verbindungsvektor \(\overrightarrow{PQ}\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren). Die Punkte \(P\) und \(Q\) dürfen also nicht auf einer Lotgerade zur Ebene \(E\) liegen.

 

\[\overrightarrow{PQ} \neq k \cdot \overrightarrow{n}_{E}; \; k \in \mathbb R\]

 

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Verbindungsvektor \(\overrightarrow{PQ}\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{n}_{F} = \overrightarrow{n}_{E} \times \overrightarrow{PQ}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{n}_{E} \times \overrightarrow{PQ}\) ist ebenfalls ein Normalenvektor der Ebene \(F\).

 

Als Aufpunkt der orthogonalen Ebene \(F\) wählt man einen der Punkte \(P\) oder \(Q\).

 

\(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{P}) = 0\) oder \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{Q})\)

 

Beispiel:

Gegeben seien die Ebene \(E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\) sowie die Punkte \(P(0|0{,}5|3)\) und \(Q(-1|0|6)\).

Ermitteln Sie eine Gleichung der Ebene \(F\), welche die Punkte \(P\) und \(Q\) enthält und zur Ebene \(E\) senkrecht ist.

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\]

\(P(0|0{,}5|3)\), \(Q(-1|0|6)\)

\(P, Q \in F\), \(F \perp E\)

 

Überprüfen, ob die Punkte \(P\) und \(Q\) eine Ebene \(F \perp E\) festlegen:

Die Punkte \(P\) und \(Q\) legen eine Ebene \(F \perp E\) fest, wenn der Verbindungsvektor \(\overrightarrow{PQ}\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\]

 

\[\overrightarrow{PQ} = \overrightarrow{Q} - \overrightarrow{P} = \begin{pmatrix} -1 \\ 0 \\ 6 \end{pmatrix} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} = \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\]

 

\[\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \neq k \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}; \: k \in \mathbb R\]

 

\(\Longrightarrow \quad\)\(\overrightarrow{PQ}\) und \(\overrightarrow{n}_{E}\) sind linear unabhängig.

\(\Longrightarrow \quad\)Die Punkte \(P\) und \(Q\) legen eine Ebene \(F \perp E\) fest.

 

Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) berechnen:

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Verbindungsvektor \(\overrightarrow{PQ}\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\begin{align*} \overrightarrow{n}_{E} \times \overrightarrow{PQ} &= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \times \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 & \cdot & 3 & - & 3 & \cdot & (-0{,}5) \\ 3 & \cdot & (-1) & - & 1 & \cdot & 3 \\ 1 & \cdot & (-0{,}5) & - & 2 & \cdot & (-1) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 7{,}5 \\ -6 \\ 1{,}5 \end{pmatrix} \\[0.8em] &= 1{,}5 \cdot \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \end{align*}\]

 

\[\Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

Gleichung der Ebene \(F\) formulieren:

Als Aufpunkt der Gleichung der Ebene \(F\) in Normalenform in Vektordarstellung dient der Punkt \(P\) oder der Punkt \(Q\).

 

\(P(0|0{,}5|3)\), \(Q(-1|0|6)\), \(\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\)

 

\[F \colon \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} \right] = 0\]

oder

\[F \colon\begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -1 \\ 0 \\ 6 \end{pmatrix} \right] = 0\]

 

\(F \perp E\) überprüfen (Probe):

Mithilfe des Skalarprodukts senkrechter Vektoren überprüft man die Aussage \(F \perp E\) (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[\overrightarrow{n}_{F} \circ \overrightarrow{n}_{E} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{F} \perp \overrightarrow{E}, \; F \perp E\]

 

\[\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}; \;\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 2 + 1 \cdot 3 = 0\]

 

\[\Longrightarrow \quad F \perp E\]

 

Orthogonale Ebene \(F\), welche eine Gerade \(g\) enthält, zu einer Ebene \(E\)

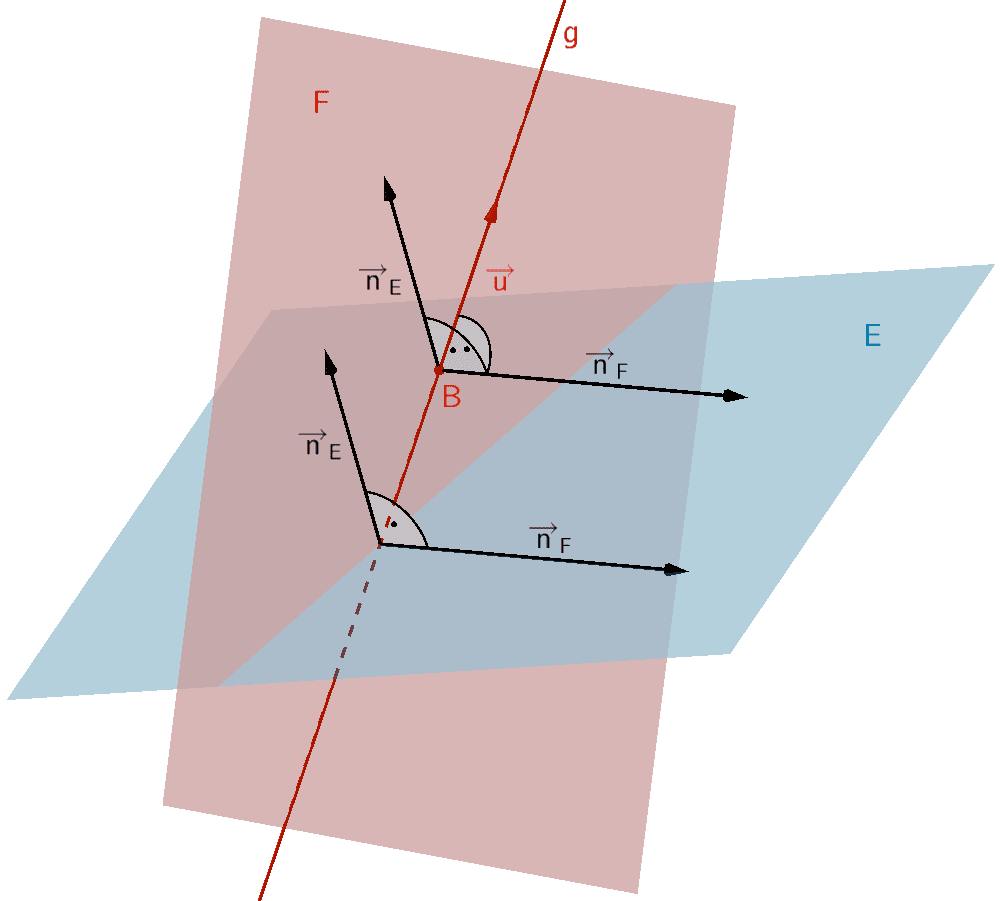
Eine orthogonale Ebene \(F\) zu einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) ist durch eine Gerade \(g \colon \overrightarrow{X} = \overrightarrow{B} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) mit \(g \subset F\) eindeutig festgelegt, wenn der Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren). Die Gerade \(g\) darf also keine Lotgerade zur Ebene \(E\) sein.

 

\[\overrightarrow{u} \neq k \cdot \overrightarrow{n}_{E}; \; k \in \mathbb R\]

 

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{n}_{F} = \overrightarrow{n}_{E} \times \overrightarrow{u}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{n}_{E} \times \overrightarrow{u}\) ist ebenfalls ein Normalenvektor der Ebene \(F\).

 

Als Aufpunkt der orthogonalen Ebene \(F\) wählt man zweckmäßig den Aufpunkt \(B\) der Gerade \(g\).

 

\[F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\]

 

Beispiel:

Gegeben seien die Ebene \(E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\) sowie die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\,; \; \lambda \in \mathbb R\).

Ermitteln Sie eine Gleichung der Ebene \(F\), welche die Gerade \(g\) enthält und zur Ebene \(E\) senkrecht ist.

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\]

\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\,; \; \lambda \in \mathbb R\]

\(g \subset F\), \(F \perp E\)

 

Überprüfen, ob die Gerade \(g\) eine Ebene \(F \perp E\) festlegt:

Die Gerade \(g\) legt eine Ebene \(F \perp E\) fest, wenn der Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\]

\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\]

 

\[\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \neq k \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}; \: k \in \mathbb R\]

 

\(\Longrightarrow \quad\)\(\overrightarrow{u}\) und \(\overrightarrow{n}_{E}\) sind linear unabhängig.

\(\Longrightarrow \quad\)Die Gerade \(g\) legt eine Ebene \(F \perp E\) fest.

 

Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) berechnen:

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Richtungsvektor \(\overrightarrow{u}\) der Geraden \(g\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\begin{align*} \overrightarrow{n}_{E} \times \overrightarrow{u} &= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \times \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 & \cdot & 3 & - & 3 & \cdot & (-0{,}5) \\ 3 & \cdot & (-1) & - & 1 & \cdot & 3 \\ 1 & \cdot & (-0{,}5) & - & 2 & \cdot & (-1) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 7{,}5 \\ -6 \\ 1{,}5 \end{pmatrix} \\[0.8em] &= 1{,}5 \cdot \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \end{align*}\]

 

\[\Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

Gleichung der Ebene \(F\) formulieren:

Als Aufpunkt der Gleichung der Ebene \(F\) in Normalenform in Vektordarstellung dient der Aufpunkt der Geradengleichung von \(g\).

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \quad \Longrightarrow \quad (0|0{,}5|3) \in g\]

\(\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\)

 

\[F \colon \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} \right] = 0\]

 

\(F \perp E\) überprüfen (Probe):

Mithilfe des Skalarprodukts senkrechter Vektoren überprüft man die Aussage \(F \perp E\) (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[\overrightarrow{n}_{F} \circ \overrightarrow{n}_{E} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{F} \perp \overrightarrow{E}, \; F \perp E\]

 

\[\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}; \;\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 2 + 1 \cdot 3 = 0\]

 

\[\Longrightarrow \quad F \perp E\]

 

Orthogonale Ebene \(G\) durch einen Punkt \(P\) zu zwei Ebenen \(E\) und \(F\)

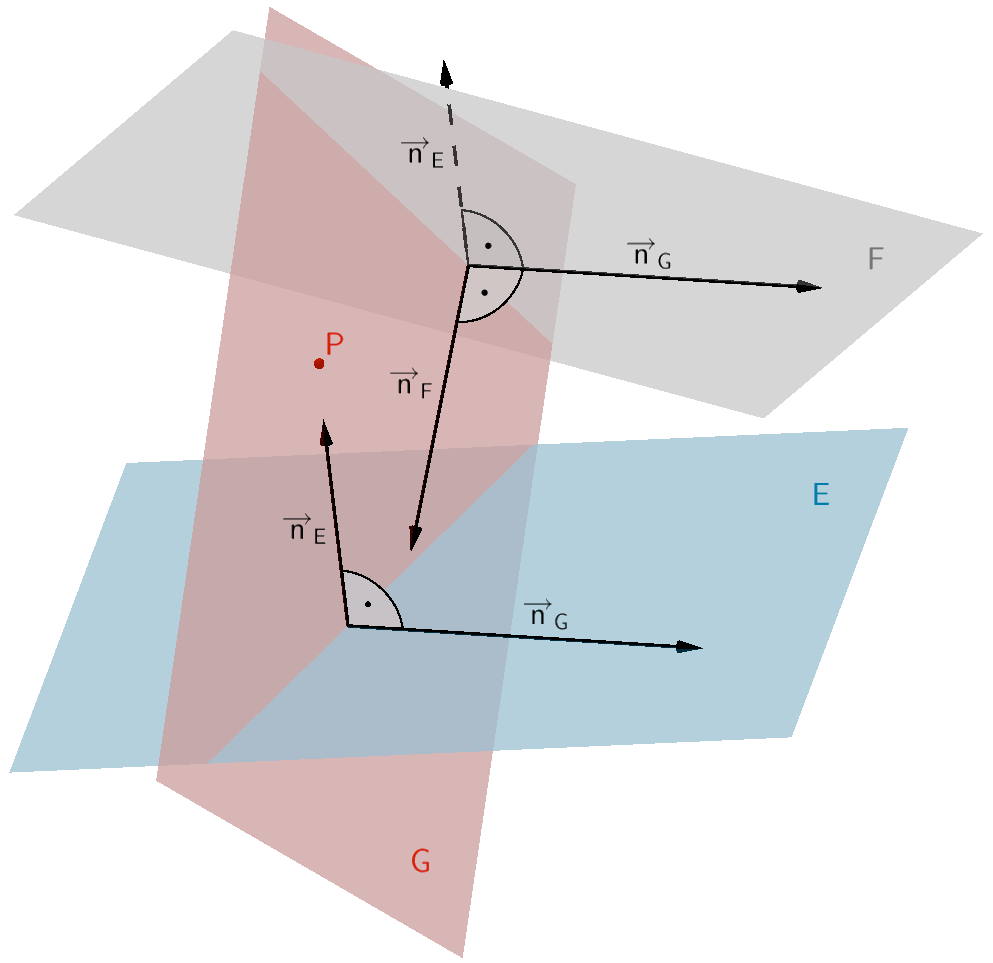
Eine orthogonale Ebene \(G\) zu zwei nicht parallelen Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B})\) ist durch einen Punkte \(P \in G\) eindeutig festgelegt.

 

\[E \nparallel F \quad \Longrightarrow \quad \overrightarrow{n}_{E} \neq k \cdot \overrightarrow{n}_{F}; \; k \in \mathbb R\]

 

Der Normalenvektor \(\overrightarrow{n}_{G}\) der orthogonalen Ebene \(G\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{n}_{G} = \overrightarrow{n}_{E} \times \overrightarrow{n}_{F}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{n}_{E} \times \overrightarrow{n}_{F}\) ist ebenfalls ein Normalenvektor der Ebene \(G\).

 

Als Aufpunkt der orthogonalen Ebene \(G\) wählt man zweckmäßig Punkt \(P\).

 

\(G \colon \overrightarrow{n}_{G} \circ (\overrightarrow{X} - \overrightarrow{P}) = 0\)

 

Beispiel:

Gegeben seien die Ebene \(E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\) und die Ebene \(F \colon x_{1} - 5x_{3} - 35 = 0\) sowie der Punkt \(P(0|0{,}5|3)\).

Ermitteln Sie eine Gleichung der Ebene \(G\), welche den Punkte \(P\) enthält und zu den Ebenen \(E\) und \(F\) senkrecht ist.

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\]

\[F \colon x_{1} - 5x_{3} - 35 = 0\]

\[P(0|0{,}5|3)\]

\(P \in G\), \(G \perp E\), \(G \perp F\)

 

Überprüfen, ob die Ebenen \(E\) und \(F\) sowie der Punkt \(P\) eine Ebene \(G \perp E, \,G \perp F\) festlegen:

Die Ebenen \(E\) und \(F\) sowie der Punkt \(P\) legen eine Ebene \(G \perp E, \,G \perp F\) fest, wenn der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und der Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\]

\[F \colon x_{1} - 5x_{3} - 35 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix}\]

 

\[\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \neq k \cdot \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix}; \: k \in \mathbb R\]

 

\(\Longrightarrow \quad\)\(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) sind linear unabhängig \((E \nparallel F)\).

\(\Longrightarrow \quad\)Die Ebenen \(E\) und \(F\) sowie der Punkt \(P\) legen eine Ebene \(G \perp E, \,G \perp F\) fest.

 

Normalenvektor \(\overrightarrow{n}_{G}\) der Ebene \(G\) berechnen:

Der Normalenvektor \(\overrightarrow{n}_{G}\) der orthogonalen Ebene \(G\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und dem Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\begin{align*} \overrightarrow{n}_{E} \times \overrightarrow{n}_{F} &= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \times \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 & \cdot & (-5) & - & 3 & \cdot & 0 \\ 3 & \cdot & 1 & - & 1 & \cdot & (-5) \\ 1 & \cdot & 0 & - & 1 & \cdot & 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -10 \\ 8 \\ -2 \end{pmatrix} \\[0.8em] &= (-2) \cdot \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \end{align*}\]

 

\[\Longrightarrow \quad \overrightarrow{n}_{G} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

Gleichung der Ebene \(G\) formulieren:

Als Aufpunkt der Gleichung der Ebene \(G\) in Normalenform in Vektordarstellung dient der Punkt \(P\).

 

\(P(0|0{,}5|3)\), \(\overrightarrow{n}_{G} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\)

 

\[G \colon \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} \right] = 0\]

 

\(G \perp E, \, G \perp F\) überprüfen (Probe):

Mithilfe des Skalarprodukts senkrechter Vektoren überprüft man die Aussage \(G \perp E, \, G \perp F\) (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[\overrightarrow{n}_{G} \circ \overrightarrow{n}_{E} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{G} \perp \overrightarrow{E}, \; G \perp E\]

\[\overrightarrow{n}_{G} \circ \overrightarrow{n}_{F} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{G} \perp \overrightarrow{F}, \; G \perp F\]

 

\[\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}; \;\overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix}; \; \overrightarrow{n}_{G} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 2 + 1 \cdot 3 = 0\]

 

\[\Longrightarrow \quad G \perp E\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 0 + 1 \cdot (-5) = 0\]

 

\[\Longrightarrow \quad G \perp F\]