Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{8x}{x^{2} + 4}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Überprüfen Sie das Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems.
b) Bestimmen Sie den maximalen Definitionsbereich der Funktion \(f\) und ermitteln Sie das Verhalten von \(f\) an den Rändern des Definitionsbereichs. Geben Sie die Gleichungen aller Asymptoten von \(G_{f}\) an.
c) Weisen Sie nach, dass der Graph \(G_{f}\) durch den Koordinatenursprung \(O(0|0)\) verläuft und berechnen Sie die Größe des Winkels, unter dem \(G_{f}\) die \(x\)-Achse schneidet.
(Teilergebnis: \(f'(x) = -\dfrac{8(x^{2} - 4)}{(x^{2} + 4)^{2}}\))
d) Bestimmen Sie die Lage und die Art der Extrempunkte von \(G_{f}\).
e) Zeichnen Sie den Graphen \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
a) Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems
Man bestimmt den Funktionsterm \(f(-x)\). Gilt \(f(-x) = f(x)\), ist \(G_{f}\) achsensymmetrisch zur \(y\)-Achse. Gilt \(f(-x) = -f(x)\), ist \(G_{f}\) punktsymmetrisch zum Koordinatenursprung \(O(0|0)\). Trifft keiner der beiden Fälle zu, zeigt \(G_{f}\) keine Symmetrie bezüglich des Koordinatensystems.
Symmetrieverhalten von Funktionsgraphen bzgl. des Koordinatensystems
\(f(-x) = f(x) \hspace{32px} \Longrightarrow \quad G_f\) ist achsensymmetrisch zur \(y\)-Achse
\(f(-x) = -f(x) \hspace{20px} \Longrightarrow \quad G_f\) ist punktsymmetrisch zum Ursprung
\[f(x) = \frac{8x}{x^{2} + 4}\]
\[f(-x) = \frac{8 \cdot (-x)}{(-x)^{2} + 4} = -\frac{8x}{x^{2} + 4} = -f(x)\]
\(\Longrightarrow \quad G_{f}\) ist Punktsymmetrisch bezüglich des Koordinatenursprungs \(O(0|0)\).
b) Maximaler Definitionsbereich von \(f\), Verhalten von \(f\) an den Rändern des Definitionsbereichs sowie Gleichungen aller Asymptoten von \(G_{f}\)
Maximaler Definitionsbereich von \(f\)
\[f(x) = \frac{8x}{\underbrace{x^{2} + 4}_{>\,0}}\]
Gebrochenrationale Funktionen sind an den Nullstellen des Nenners nicht definiert. Da der Nenner der gebrochenrationonalen Funktion \(f\) für alle \(x \in \mathbb R\) größer als Null ist, folgt:
\[D_{f} = \mathbb R\]
Verhalten von \(f\) an den Rändern des Definitionsbereichs
\[f(x) = \frac{8x}{x^{2} + 4}; \; D_{f} = \mathbb R = \; ]-\infty;+\infty[\]
Es ist das Verhalten von \(f\) für \(x \to -\infty\) und \(x \to +\infty\) zu untersuchen.
Die Grenzwertbetrachtung \(\lim \limits_{x\,\to\,\pm\infty} f(x)\) führt auf den unbestimmten Ausdruck \(\pm\frac{\infty}{\infty}\). Für eine aussagekräftige Grenzwertbetrachtung wird die höchste Potenz des Nenners von \(f\) im Zähler und im Nenner ausgeklammert und gekürzt. Der verbleibende Funktionsterm erlaubt eine eindeutige Grenzwertbetrachtung.
\[\begin{align*}\lim \limits_{x\,\to\,-\infty} f(x) &= \lim \limits_{x \, \to \, -\infty} \frac{\overbrace{8x}^{\to\,-\infty}}{\underbrace{x^{2} + 4}_{\to\,+\infty }}\\[0.8em] &= \lim \limits_{x\,\to\,-\infty} \frac{\cancel{x^{2}} \cdot \left( \frac{8}{x}\right)}{\cancel{x^{2}} \cdot \left( 1 + \frac{4}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x\,\to\,-\infty} \frac{\overbrace{\frac{8}{x}}^{\to\,0}}{1 + \underbrace{\frac{4}{x^{2}}}_{\to\,0}} \\[0.8em] &= 0 \end{align*}\]
\[\begin{align*}\lim \limits_{x\,\to\,+\infty} f(x) &= \lim \limits_{x \, \to \, +\infty} \frac{\overbrace{8x}^{\to\,+\infty}}{\underbrace{x^{2} + 4}_{\to\,+\infty }}\\[0.8em] &= \lim \limits_{x\,\to\,+\infty} \frac{\cancel{x^{2}} \cdot \left( \frac{8}{x}\right)}{\cancel{x^{2}} \cdot \left( 1 + \frac{4}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x\,\to\,+\infty} \frac{\overbrace{\frac{8}{x}}^{\to\,0}}{1 + \underbrace{\frac{4}{x^{2}}}_{\to\,0}} \\[0.8em] &= 0 \end{align*}\]
Alternative: Grad des Zähler- und Nennerpolynoms betrachten:
Der Grad des Zählerpolynoms der gebrochenrationalen Funktion \(f\) ist mit \(8x\) kleiner als der Grad des Nennerpolynoms \(x^{2} + 4\). Daraus lässt sich schlussfolgern, dass \(G_{f}\) die \(x\)-Achse mit der Gleichung \(y = 0\) als waagrechte Asymptote für das Verhalten im Unendlichen besitzt.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\[f(x) = \frac{\overbrace{8x}^{\large{\text{Grad 1}}}}{\underbrace{x^{2} + 4}_{\large{\text{Grad 2}}}}\]
\(\Longrightarrow \quad G_{f}\) besitzt die waagrechte Asymptote \(y = 0\) (\(x\)-Achse).
Gleichungen aller Asymptoten von \(G_{f}\)
Die gebrochenrationale Funktion \(f\) ist in \(\mathbb R\) definiert. Es existieren keine Polstellen und somit auch keine senkrechten Asymptoten von \(G_{f}\). Die \(x\)-Achse mit der Gleichung \(y = 0\) ist die einzige (waagrechte) Asymptote von \(G_{f}\).
c) Nachweis, dass \(G_{f}\) durch den Koordinatenursprung \(O(0|0)\) verläuft sowie Winkel, unter dem \(G_{f}\) die \(x\)-Achse schneidet
Nachweis, dass \(G_{f}\) durch den Koordinatenursprung \(0(0|0)\) verläuft
Es muss \(f(0) = 0\) gelten.
\[f(x) = \frac{8x}{x^{2} + 4}; \; D_{f} = \mathbb R\]
\[f(0) = \frac{8 \cdot 0}{0^{2} + 4} = 0\]
\(\Longrightarrow \quad G_{f}\) verläuft durch den Koordinatenursprung \(O(0|0)\).
Größe des Winkels, unter dem \(G_{f}\) die \(x\)-Achse schneidet
Der Winkel unter dem \(G_{f}\) die \(x\)-Achse schneidet ist gleich dem spitzen Winkel, den die Tangente \(T\) an \(G_{f}\) im Koordinatenursprung \(O(0|0)\) mit der \(x\)-Achse einschließt. Im Falle einer positiven Tangentensteigung entspricht der Schnittwinkel dem Steigungswinkel der Tangente.
Für den Steigungswinkel \(\alpha\) einer Geraden mit der Steigung \(m\) gilt:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\tan{\alpha} = m\]
Für den Steigungswinkel \(\alpha\) der Tangente \(T\) an \(G_{f}\) gilt folglich:
\[\tan{\alpha} = m_{T}\]
Die erste Ableitung \(f'\) an der Stelle \(x = 0\) berechnet die Steigung \(m_{T}\) der Tangente \(T\) an \(G_{f}\) im Koordinatenursprung \(O(0|0)\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = f'(0)\]
Mit \(\tan{\alpha} = m_{T}\) folgt:
\[\tan{\alpha} = f'(0)\]
Erste Ableitung \(f'\) bilden:
Die Funktion \(f\) wird mithilfe der Quotientenregel, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel abgeleitet.
\[f(x) = \frac{8x}{x^{2} + 4}; \; D_{f} = \mathbb R\]
Quotientenregel
\[f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\left[ \frac{u(x)}{v(x)} \right]' = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{\left[ v(x) \right]^{2}}\]
\[u(x) = 8x; \; u'(x) = 8\]
\[v(x) = x^{2} + 4; \, v'(x) = 2x + 0 = 2x\]
\[\begin{align*} f'(x) &= \frac{8 \cdot (x^{2} + 4) - 8x \cdot 2x}{(x^{2} + 4)^{2}} \\[0.8em] &= \frac{8x^{2} + 32 - 16x^{2}}{(x^{2} + 4)^{2}} \\[0.8em] &= \frac{-8x^{2} + 32}{(x^{2} + 4)^{2}} \\[0.8em] &= -\frac{8(x^{2} - 4)}{(x^{2} + 4)^{2}} \end{align*}\]
Steigungswinkel \(\alpha\) der Tangente \(T\) an \(G_{f}\) berechnen:
\[\begin{align*} \tan{\alpha} &= f'(0) \\[0.8em] &= -\frac{8(0^{2} - 4)}{(0^{2} + 4)^{2}} \\[0.8em] &= \frac{32}{16} \\[0.8em] &= 2 & &| \; \text{TR:} \; \tan^{-1}(\dots) \\[3.2em] \alpha &\approx 63{,}43^{\circ} \end{align*}\]
Der Graph \(G_{f}\) der Funktion \(f\) schneidet die \(x\)-Achse im Koordinatenursprung unter einem Winkel von ca. 63,43°.
d) Lage und Art der Extrempunkte von \(G_{f}\)
An den Extremstellen besitzt der Graph der Funktion \(f\) eine waagrechte Tangente, das heißt, die Tangentensteigung ist gleich Null. Die erste Ableitung \(f'\) der Funktion \(f\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\),
Folglich lautet die notwendige Bedingung für einen Extrempunkt von \(G_{f}\):
\[f'(x) = 0\]
Der Funktionsterm \(f'(x)\) ist bereits aus Teilaufgabe c bekannt.
\[f'(x) = -\frac{8(x^{2} - 4)}{(x^{2} + 4)^{2}}\]
Nullstellen von \(f'\) bestimmen:
Ein Bruchterm ist gleich Null, wenn der Zählerterm gleich Null ist.
\[\begin{align*}f'(x) = 0 \quad \Longrightarrow \quad x^{2} - 4 &= 0 & &| + 4 \\[0.8em] x^{2} &= 4 & &| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm2\end{align*}\]
An den Stellen \(x_{1} = -2\) und \(x_{2} = 2\) besitzt \(G_{f}\) jeweils eine waagrechte Tangente, welche auf einen Extrem- oder Terrassenpunkt hinweist.
Nachweis der Extrempunkte und deren Art:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
Ein Extrempunkt liegt an den Stellen \(x_{1} = -2\) und \(x_{2} = 2\) dann vor, wenn \(f'\) dort das Vorzeichen wechselt, das heißt, wenn \(G_{f}\) gemäß dem Monotoniekriterium das Monotonieverhalten ändert.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[f'(x) = -\frac{8(x^{2} - 4)}{\underbrace{(x^{2} + 4)^{2}}_{>\,0}}\]
Der Zähler von \(f'(x)\) bestimmt den Vorzeichenwechsel von \(f'\) in der Umgebung der Stelle \(x_{1} = -2\) bzw. \(x_{2} = 2\).
\(8(x^{2} - 4) < 0\) für \(x > -2\) bzw. \(x < 2\)
\(8(x^{2} - 4) > 0\) für \(x < -2\) bzw. \(x > 2\)
Somit ergibt sich:
\[\left. \begin{align*} &f'(x) < 0 \; \text{für} \; x < -2 \\[0.8em] &f'(-2) = 0 \\[0.8em] &f'(x) > 0 \; \text{für} \; x > -2 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}\;TiP(-2|f(-2))\]
\[\left. \begin{align*} &f'(x) > 0 \; \text{für} \; x < 2 \\[0.8em] &f'(2) = 0 \\[0.8em] &f'(x) < 0 \; \text{für} \; x > 2 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}\;HoP(2|f(2))\]
Veranschaulichung mit einer Monotonietabelle:
\[f'(x) = -\frac{8(x^{2} - 4)}{\underbrace{(x^{2} + 4)^{2}}_{>\,0}}\]
| \(x\) | \(x < -2\) | \(x = -2\) | \(x > -2\) |
| \(8(x^{2} - 4)\) | \(+\) | \(0\) | \(-\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\searrow\) | \(TiP(-2|f(-2))\) | \(\nearrow\) |
| \(x\) | \(x < 2\) | \(x = 2\) | \(x > 2\) |
| \(8(x^{2} - 4)\) | \(-\) | \(0\) | \(+\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f}\) | \(\nearrow\) | \(HoP(2|f(2))\) | \(\searrow\) |
\(y\)-Koordinate der Extrempunkte berechnen:
\[f(x) = \frac{8x}{x^{2} + 4}; \; D_{f} = \mathbb R\]
\[f(-2) = \frac{8 \cdot -2}{(-2)^{2} + 4} = \frac{-16}{8} = -2\]
\[\Longrightarrow \quad TiP(-2|-2)\]
\[f(2) = \frac{8 \cdot 2}{2^{2} + 4} = \frac{16}{8} = 2\]
\[\Longrightarrow \quad HoP(2|2)\]
Anmerkung:
Es ist ebenso möglich, zunächst die Lage und Art von nur einem der beiden Extrempunkte zu bestimmen und anschließend aufgrund der in Teilaufgabe a festgestellten Punktsymmetrie zum Koordinatenursprung von \(f\) auf die Lage und Art des jeweils anderen Extrempunkts zu schließen.
e) Zeichnen von \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse:
- \(G_{f}\) ist punktsymmetrisch zum Koordinatenursprung \(O(0|0)\) (vgl. Teilaufgabe a)
- \(D_{f} = \mathbb R\) (vgl Teilaufgabe b)
- Für \(x \to \pm \infty\) besitzt \(G_{f}\) die \(x\)-Achse als waagrechte Asymptote mit der Gleichung \(y = 0\) (vgl. Teilaufgabe b).
- \(G_{f}\) schneidet die \(x\)-Achse im Koordinatenursprung \(O(0|0)\) unter einem Winkel von ca. \(63{,}43^{\circ}\) (vgl. Teilaufgabe c).
- \(G_{f}\) besitzt den Tiefpunkt \(TiP(-2|-2)\) und den Hochpunkt \(HoP(2|2)\) (vgl. Teilaufgabe d).
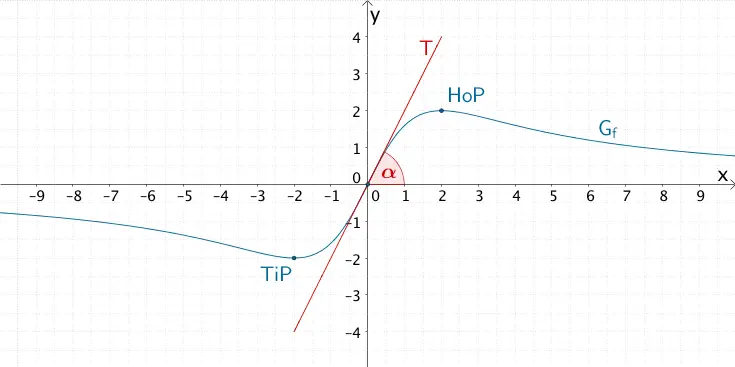
Verlauf des Graphen \(G_{f}\) der in \(\mathbb R\) definierten gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{8x}{x^{2} + 4}\), Extrempunkte, Schnittwinkel \(\alpha\), unter dem \(G_{f}\) die \(x\)-Achse im Koordinatenursprung schneidet


