Der Graph von \(f\), die \(x\)-Achse und die Gerade \(x = u\) mit \(u \in \mathbb R^+\) schließen für \(0 \leq x \leq u\) ein Flächenstück mit dem Inhalt \(A(u)\) ein.
Zeigen Sie, dass \(A(u) = 2 - 2e^{-0{,}5u^2}\) gilt. Geben Sie \(\lim \limits_{u \, \to \, + \infty} A(u)\) an und deuten Sie das Ergebnis geometrisch.
(6 BE)
Lösung zu Teilaufgabe 1d
Nachweis, dass \(\displaystyle A(u) = 2 - 2e^{-0{,}5u^2}\) gilt
1. Lösungsansatz: Hauptsatz der Differential- und Integralrechnung (HDI) anwenden
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\(\displaystyle F(u) = \int_0^u f(x)\,dx = 2 - 2e^{-0{,}5u^2}\) (siehe Angabe)
\[f(u) = 2u \cdot e^{-0{,}5u^2}\]
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
\[F'(u) = f(u)\]
\[\begin{align*} F'(u) &= \left( 2 - 2e^{-0{,}5u^2} \right)' \\[0.8em] &= 0 - 2e^{-0{,}5u^2} \cdot (-0{,}5) \cdot 2u \\[0.8em] &= 2u \cdot e^{-0{,}5u^2} \\[0.8em] &= f(u) \end{align*}\]
2. Lösungsansatz: Integral \(\displaystyle \int_0^u f(x)\,dx\) bestimmen
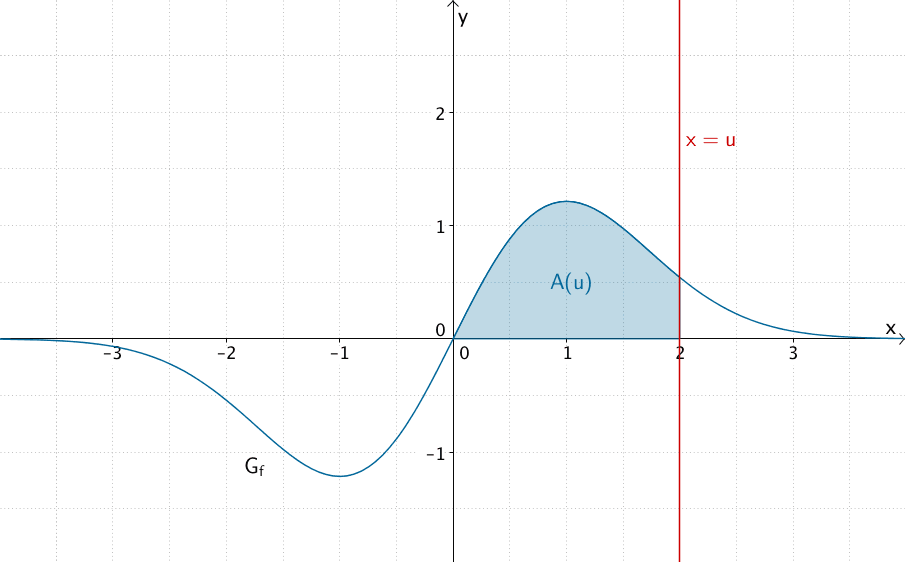
Die Maßzahl des Flächeninhalts \(A(u)\) des Flächenstücks, welches der Graph von \(f\) mit der \(x\)-Achse und der Geraden \(x = u\) mit \(u \in \mathbb R^+\) für \(0 \leq x \leq u\) einschließt, ist gleich dem Wert des bestimmten Integrals \(\displaystyle \int_0^u f(x)\, dx\).
\[A(u) = \int_0^u f(x)\, dx\,; \quad u \in \mathbb R^+\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Stammfunktion \(F(x)\) von \(f(x)\) bestimmen:
\[f(x) = 2x \cdot e^{-0{,}5x^2}\]
Wichtiges unbestimmtes Integral:
\[\int f'(x) \cdot e^{f(x)}dx = e^{f(x)} + C\]
(vgl. Merkhilfe)
Mit \(g(x) = -0{,}5x^2\) und \(g'(x) = -x\) folgt:
\[f(x) = -2 \cdot g'(x) \cdot e^{\,g(x)} = -2 \cdot (-x) \cdot e^{-0{,}5x^2}\]
\[F(x) = -2 \cdot e^{-0{,}5x^2} + C\]
Flächeninhalt \(A(u)\) bestimmen:
\[\begin{align*} A(u) &= \int_0^u f(x)\,dx \\[0.8em] &= \left[ -2 \cdot e^{-0{,}5x^2} \right]_0^u \\[0.8em] &= -2 \cdot e^{-0{,}5 \cdot u^2} - \left( -2 \cdot e^{-0{,}5 \cdot 0^2} \right) \\[0.8em] &= -2 \cdot e^{-0{,}5u^2} + 2 \\[0.8em] &= 2 - 2e^{-0{,}5u^2} \end{align*}\]
Grenzwert \(\displaystyle \lim \limits_{u \, \to \, + \infty} A(u)\)
\[\lim \limits_{u \, \to \, + \infty} A(u) = \lim \limits_{u \, \to \, + \infty} \biggl( 2 - \underbrace{2e^{-0{,}5u^2}}_{\to \, 0} \biggr) = 2\]
Geometrische Deutung:
Der Flächeninhalt der vom Graphen der Funktion \(f\) und der positiven \(x\)-Achse eingeschlossenen, sich ins Unendliche erstreckenden Fläche, ist mit 2 FE (Flächeneinheiten) endlich.

