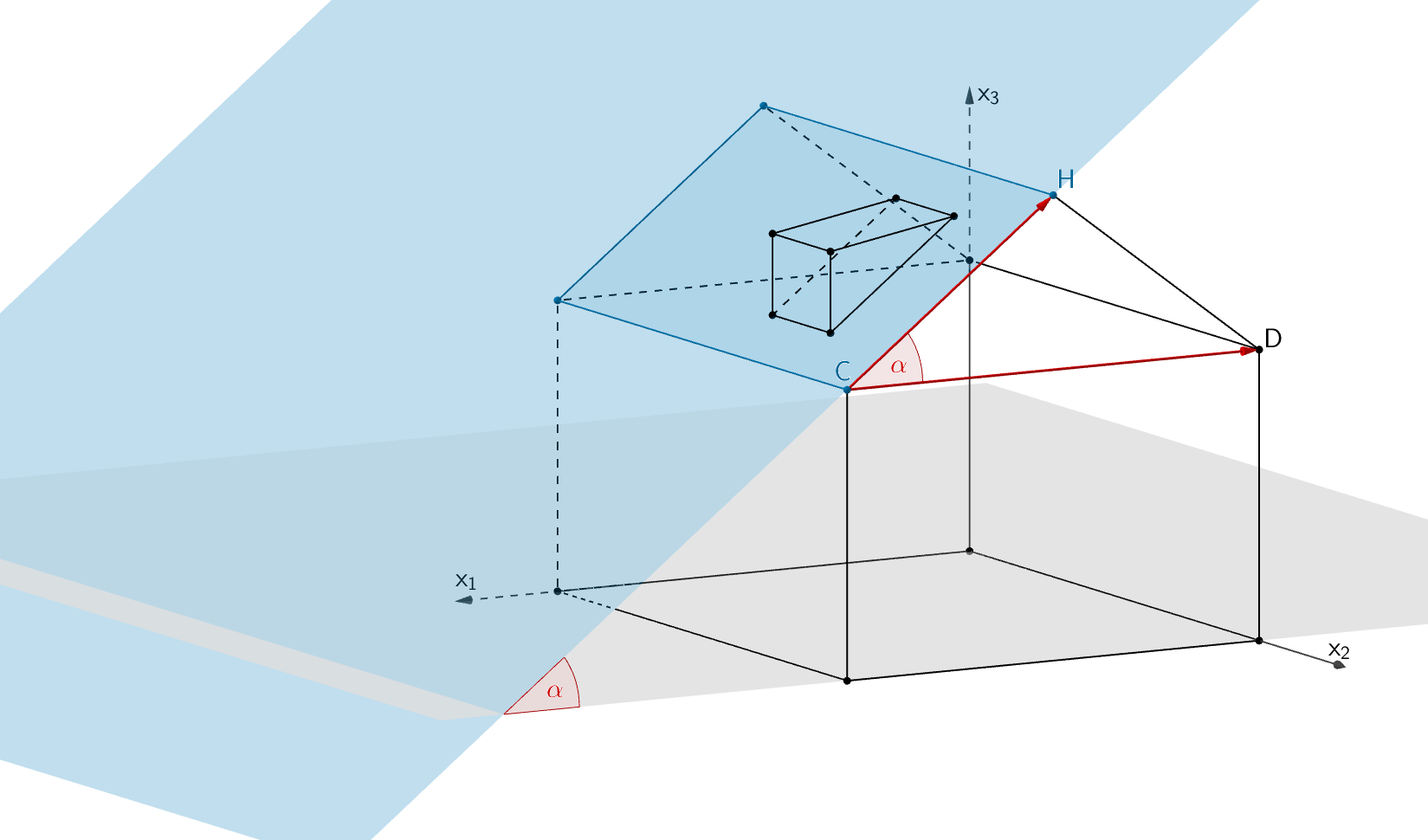
In der Stadt, in der das Einfamilienhaus steht, gilt für die Errichtung von Dachgauben eine Satzung, die jeder Bauherr einhalten muss. Diese Satzung lässt die Errichtung einer Dachgaube zu, wenn die Größe des Neigungswinkels der Dachfläche des jeweiligen Hausdachs gegen die Horizontale mindestens 35° beträgt. Zeigen Sie rechnerisch, dass für das betrachtete Einfamilienhaus die Errichtung einer Dachgaube zulässig ist.
(3 BE)
Lösung zu Teilaufgabe b
Der Neigungswinkel der Dachfläche, auf der die Dachgaube errichtet werden soll (Rechteck \(BCHG\)), entspricht beispielsweise dem Winkel \(\alpha\) zwischen den Vektoren \(\overrightarrow{CD}\) und \(\overrightarrow{CH}\).
Anwendung des Skalarprodukts:
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
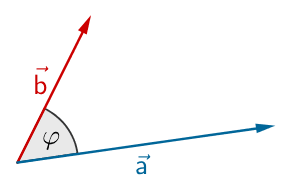
\[\cos \varphi = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert}\,; \quad \varphi \in [0;\pi]\]
\[ \cos{\alpha} = \frac{\overrightarrow{CD} \circ \overrightarrow{CH}}{\vert \overrightarrow{CD} \vert \cdot \vert \overrightarrow{CH} \vert}\]
Vektoren \(\overrightarrow{CD}\) und \(\overrightarrow{CH}\) berechnen:
\(C\,(8|10|5)\), \(D\,(0|10|5)\), \(H\,(4|10|8)\) (siehe Abbildung zur Aufgabengruppe)
\[\overrightarrow{CD} = \overrightarrow{D} - \overrightarrow{C} = \begin{pmatrix} 0 \\ 10 \\ 5 \end{pmatrix} - \begin{pmatrix} 8 \\ 10 \\ 5 \end{pmatrix} = \begin{pmatrix} -8 \\ 0 \\ 0 \end{pmatrix}\]
\[\overrightarrow{CH} = \overrightarrow{H} - \overrightarrow{C} = \begin{pmatrix} 4 \\ 10 \\ 8 \end{pmatrix} - \begin{pmatrix} 8 \\ 10 \\ 5 \end{pmatrix} = \begin{pmatrix} -4 \\ 0 \\ 3 \end{pmatrix}\]
Neigungswinkel berechnen:
\[\begin{align*} \cos{\alpha} &= \frac{\overrightarrow{CD} \circ \overrightarrow{CH}}{\vert \overrightarrow{CD} \vert \cdot \vert \overrightarrow{CH} \vert} \\[0.8em] &= \frac{\begin{pmatrix} -8 \\ 0 \\ 0 \end{pmatrix} \circ \begin{pmatrix} -4 \\ 0 \\ 3 \end{pmatrix}}{\left| \begin{pmatrix} -8 \\ 0 \\ 0 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -4 \\ 0 \\ 3 \end{pmatrix} \right|} \\[0.8em] &= \frac{(-8) \cdot (-4) + 0 \cdot 0 + 0 \cdot 3}{\sqrt{(-8)^2 + 0^2 + 0^2} \cdot \sqrt{(-4)^2 + 0^2 + 3^2}} \\[0.8em] &= \frac{32}{\sqrt{64} \cdot \sqrt{25}} \\[0.8em] &= \frac{32}{8 \cdot 5} = \frac{4}{5} & &| \;\cos^{-1}(\dots) \\[0.8em] \alpha &= 36{,}87^{\circ} \end{align*}\]
\[\Longrightarrow \quad \alpha > 35^{\circ}\]
\(\Longrightarrow \quad\) Die Errichtung einer Dachgaube ist zulässig.