Teilaufgabe 2b
Lösung zu Teilaufgabe 2b
Geradengleichung in Parameterform
Nachfolgend seien drei Möglichkeiten für ein geeignetes Koordinatensystem erläutert.
1. Möglichkeit: Punkt \(A\) liegt im Koordinatenursprung
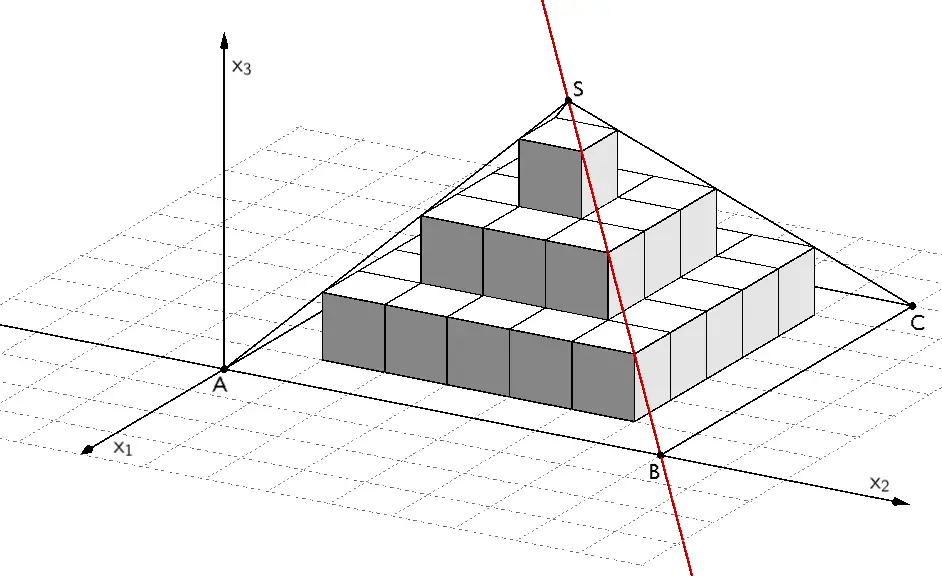
Wählt man Punkt \(A\) als Ursprung des Koordinatensystems und die Strecke \([AB]\) auf der \(x_{2}\)-Achse sowie die Strecke \([AD]\) auf der \(x_{1}\)-Achse, liegt die Pyramide \(ABCDS\) im II. Oktanten.
Koordinaten der Punkte \(B\) und \(S\) entnehmen:
\[B\,(0|7|0)\,, \enspace S\,(-3{,}5|3{,}5|3{,}5)\]
Gleichung der Geraden \(BS\) bestimmen:
Es sei \(B\) der Aufpunkt der Geradengleichung von \(BS\).
\[\begin{align*}BS \colon \overrightarrow{X} &= \overrightarrow{B} + \mu \cdot \overrightarrow{BS} \\[0.8em] BS \colon \overrightarrow{X} &= \overrightarrow{B} + \mu \cdot (\overrightarrow{S} - \overrightarrow{B}) \\[0.8em] BS \colon \overrightarrow{X} &= \begin{pmatrix} 0 \\ 7 \\ 0 \end{pmatrix} + \mu \cdot \left[\begin{pmatrix} -3{,}5 \\ 3{,}5 \\ 3{,}5 \end{pmatrix} - \begin{pmatrix} 0 \\ 7 \\ 0 \end{pmatrix} \right] \\[0.8em] BS \colon \overrightarrow{X} &= \begin{pmatrix} 0 \\ 7 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3{,}5 \\ -3{,}5 \\ 3{,}5 \end{pmatrix} \end{align*}\]
2. Möglichkeit: Punkt \(B\) liegt im Koordinatenursprung
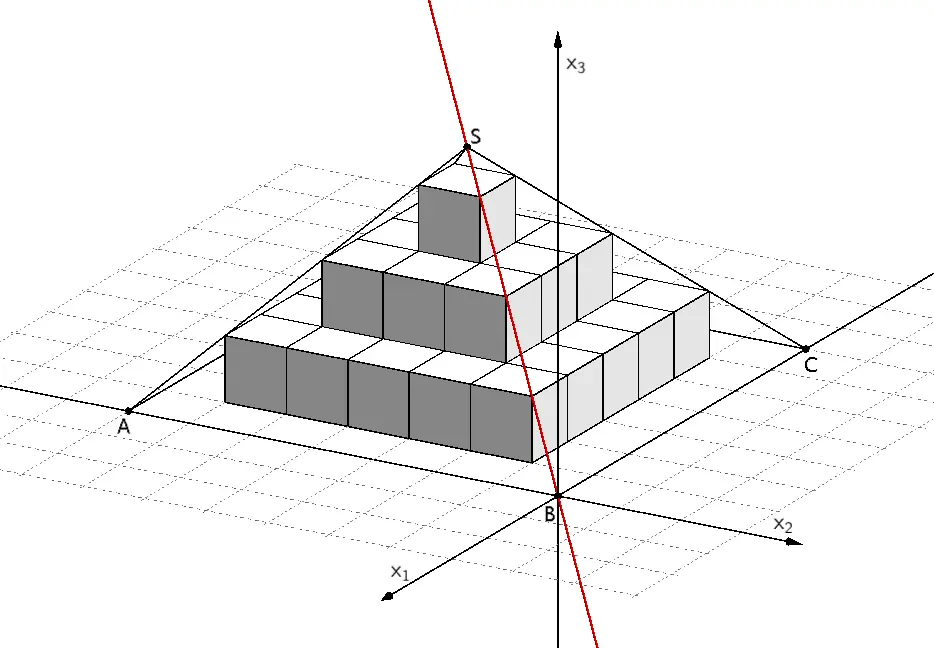
Wählt man Punkt \(B\) als Ursprung des Koordinatensystems und die Strecke \([AB]\) auf der \(x_{2}\)-Achse sowie die Strecke \([BC]\) auf der \(x_{1}\)-Achse, liegt die Pyramide \(ABCDS\) im III. Oktanten.
Koordinaten der Punkte \(B\) und \(S\) entnehmen:
\[B\,(0|0|0)\,, \enspace S\,(-3{,}5|-3{,}5|3{,}5)\]
Gleichung der Geraden \(BS\) bestimmen:
Es sei \(B\) der Aufpunkt der Geradengleichung von \(BS\).
\[\begin{align*}BS \colon \overrightarrow{X} &= \overrightarrow{B} + \lambda \cdot \overrightarrow{BS} & &| \; \overrightarrow{B} = \overrightarrow{0} \\[0.8em] BS \colon \overrightarrow{X} &= \lambda \cdot \overrightarrow{S} \\[0.8em] BS \colon \overrightarrow{X} &= \lambda \cdot \begin{pmatrix} -3{,}5 \\ -3{,}5 \\ 3{,}5 \end{pmatrix} \end{align*}\]
3. Möglichkeit: Punkt \(C\) liegt im Koordinatenursprung
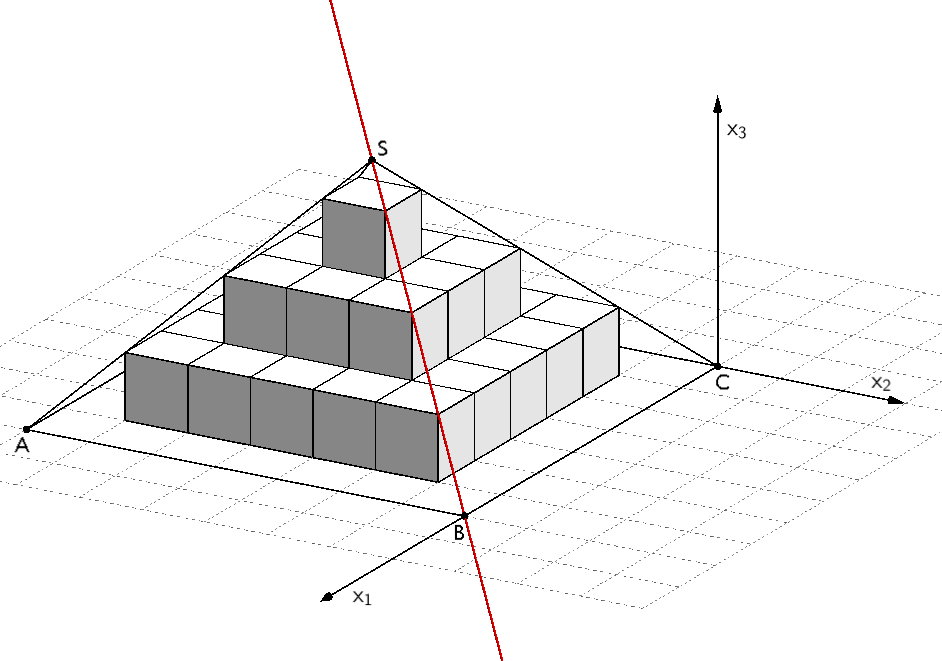
Wählt man Punkt \(C\) als Ursprung des Koordinatensystems und die Strecke \([DC]\) auf der \(x_{2}\)-Achse sowie die Strecke \([BC]\) auf der \(x_{1}\)-Achse, liegt die Pyramide \(ABCDS\) im IV. Oktanten.
Koordinaten der Punkte \(B\) und \(S\) entnehmen:
\[B\,(7|0|0)\,, \enspace S\,(3{,}5|-3{,}5|3{,}5)\]
Gleichung der Geraden \(BS\) bestimmen:
Es sei \(B\) der Aufpunkt der Geradengleichung von \(BS\).
\[\begin{align*}BS \colon \overrightarrow{X} &= \overrightarrow{B} + \nu \cdot \overrightarrow{BS} \\[0.8em] BS \colon \overrightarrow{X} &= \overrightarrow{B} + \nu \cdot (\overrightarrow{S} - \overrightarrow{B}) \\[0.8em] BS \colon \overrightarrow{X} &= \begin{pmatrix} 7 \\ 0 \\ 0 \end{pmatrix} + \nu \cdot \left[\begin{pmatrix} 3{,}5 \\ -3{,}5 \\ 3{,}5 \end{pmatrix} - \begin{pmatrix} 7 \\ 0 \\ 0 \end{pmatrix} \right] \\[0.8em] BS \colon \overrightarrow{X} &= \begin{pmatrix} 7 \\ 0 \\ 0 \end{pmatrix} + \nu \cdot \begin{pmatrix} -3{,}5 \\ -3{,}5 \\ 3{,}5 \end{pmatrix} \end{align*}\]
