Teilaufgabe a

Geometrie 2

Für die Fernsehübertragung eines Fußballspiels wird über dem Spielfeld eine bewegliche Kamera installiert. Ein Seilzugsystem, das an vier Masten befestigt wird, hält die Kamera in der gewünschten Position. Seilwinden, welche die Seile koordiniert verkürzen und verlängern, ermöglichen eine Bewegung der Kamera.

In der Abbildung ist das horizontale Spielfeld modellhaft als Rechteck in der \(x_{1}x_{2}\)-Ebene eines kartesischen Koordinatensystems dargestellt. Die Punkte \(W_{1}\), \(W_{2}\), \(W_{3}\) und \(W_{4}\) beschreiben die Positionen der vier Seilwinden. Eine Längeneinheit im Koordinatensystem entspricht 1 m in der Realität, d. h. alle vier Seilwinden sind in einer Höhe von 30 m angebracht.

Abbildung zu Geometrie 2 - Prüfungsteil B - Mathematik Abitur Bayern 2016

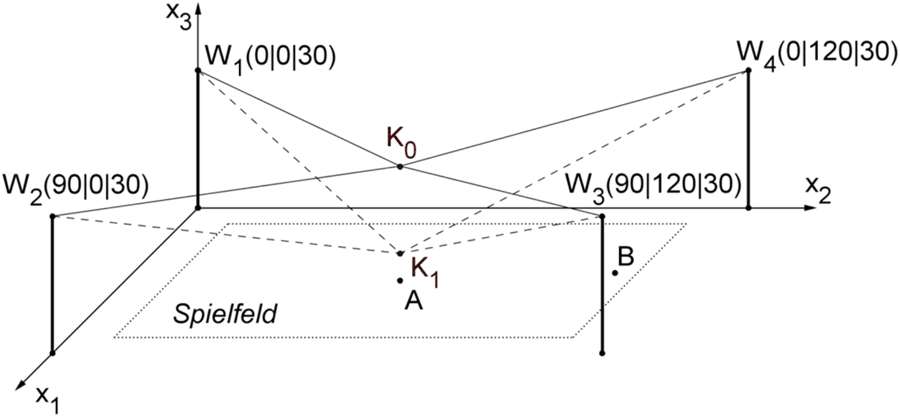
Der Punkt \(A(45|60|0)\) beschreibt die Lage des Anstoßpunkts auf dem Spielfeld. Die Kamera befindet sich zunächst in einer Höhe von 25 m vertikal über dem Anstoßpunkt. Um den Anstoß zu filmen, wird die Kamera um 19 m vertikal abgesenkt. In der Abbildung ist die ursprüngliche Kameraposition durch den Punkt \(K_{0}\), die abgesenkte Position durch den Punkt \(K_{1}\) dargestellt.

Berechnen Sie die Seillänge, die von jeder der vier Seilwinden abgerollt werden muss, um dieses Absenken zu ermöglichen, wenn man davon ausgeht, dass die Seile geradlinig verlaufen.

(4 BE)

Lösung zu Teilaufgabe a

 

Koordinaten eines Punktes, Betrag eines Vektors

 

\(W_{1}(0|0|30)\), \(W_{2}(90|0|30)\), \(W_{3}(90|120|30)\), \(W_{4}(0|120|30)\)

\(A(45|60|0)\)

 

Die Punkte \(K_{0}\) und \(K_{1}\) liegen vertikal über dem Punkt \(A\) und haben somit die gleiche \(x_{1}\)- und \(x_{2}\)-Koordinate wie der Punkt \(A\). Die \(x_{3}\)-Koordinaten der Punkte \(K_{0}\) und \(K_{1}\) entnimmt man der Angabe zu \(x_{3} = 25\) bzw. \(x_{3} = 25 - 19 = 6\).

 

\[\Longrightarrow \quad K_{0}(45|60|25), \, K_{1}(45|60|6)\]

 

Betrachtung der Ebene, in der die Punkte W₁, K₀, K₁ und A liegen.

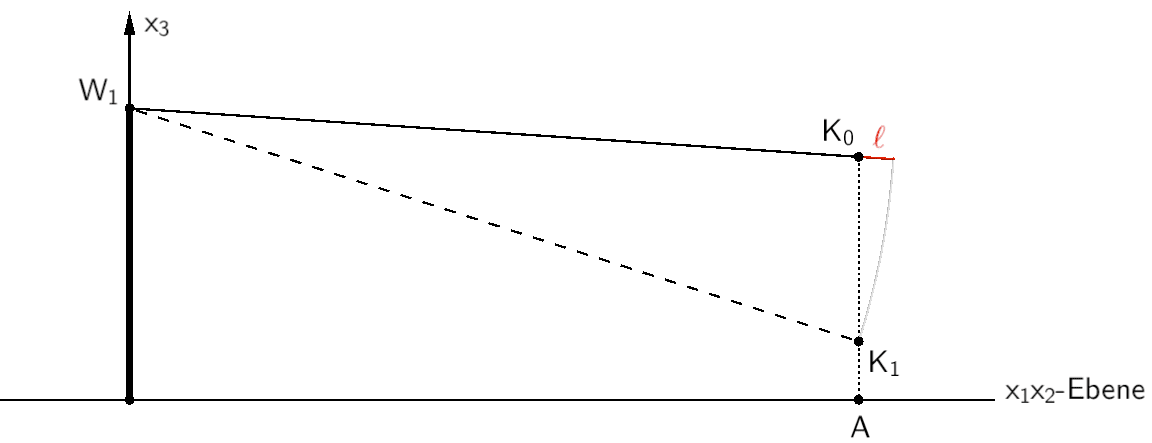
Betrachtet man beispielsweise die Punkte \(W_{1}\), \(K_{0}\) und \(K_{1}\), so ergibt sich die Seillänge \(\ell\), die von jeder der vier Seilwinden abgerollt werden muss, als die Differenz der Längen der Strecken \([W_{1}K_{1}]\) und \([W_{1}K_{0}]\). Voraussetzung: Die Seile verlaufen geradlinig (vgl. Angabe).

 

\[\ell = \overline{W_{1}K_{1}} - \overline{W_{1}K_{0}}\]

 

Längen der Strecken \([W_{1}K_{1}]\) und \([W_{1}K_{0}]\) berechnen:

\(W_{1}(0|0|30)\), \(K_{0}(45|60|25)\), \(K_{1}(45|60|6)\)

 

\[\begin{align*}\overline{W_{1}K_{1}} &= \left| \overrightarrow{W_{1}K_{1}} \right| \\[0.8em] &= \left| \overrightarrow{K_{1}} - \overrightarrow{W_{1}} \right| \\[0.8em] &= \left| \begin{pmatrix} 45 \\ 60 \\ 6 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 30 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 45 \\ 60 \\ -24 \end{pmatrix} \right| \\[0.8em] &= \sqrt{{45}^{2} + {60}^{2} + (-24)^{2}} \\[0.8em] &= \sqrt{6201} \\[0.8em] &= 3\sqrt{689} \end{align*}\]

\[\begin{align*}\overline{W_{1}K_{0}} &= \left| \overrightarrow{W_{1}K_{0}} \right| \\[0.8em] &= \left| \overrightarrow{K_{0}} - \overrightarrow{W_{1}} \right| \\[0.8em] &= \left| \begin{pmatrix} 45 \\ 60 \\ 25 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 30 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 45 \\ 60 \\ -5 \end{pmatrix} \right| \\[0.8em] &= \sqrt{{45}^{2} + {60}^{2} + (-5)^{2}} \\[0.8em] &= \sqrt{5650} \\[0.8em] & = 5\sqrt{226} \end{align*}\]

 

Seillänge \(\ell\) berechnen:

 

\[\ell = \overline{W_{1}K_{1}} - \overline{W_{1}K_{0}} = 3\sqrt{689} - 5\sqrt{226} \approx 3{,}58\]

 

Um ein vertikales Absenken der Kamera von Position \(K_{0}\) zu Position \(K_{1}\) zu bewirken, muss von jeder der vier Seilwinden die Seillänge 3,58 m abgerollt werden.

Tags
Weitere Lösungen dieser Aufgabengruppe: Teilaufgabe b »