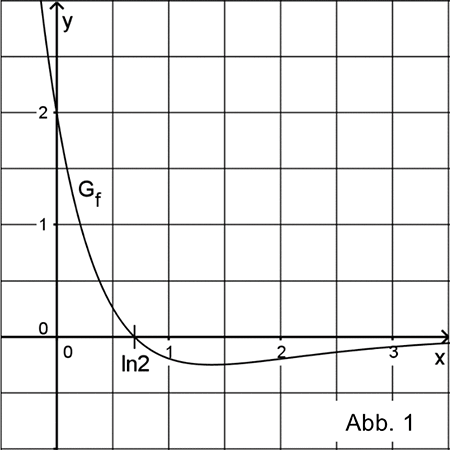
Gegeben ist die Funktion \(f\) mit \(f(x) = 2e^{-x} \cdot \left( 2e^{-x} - 1 \right)\) und \(x \in \mathbb R\). Abbildung 1 zeigt den Graphen \(G_{f}\) von \(f\) sowie die einzige Nullstelle \(x = \ln 2\) von \(f\).
Zeigen Sie, dass für den Term der Ableitungsfunktion \(f'\) von \(f\) gilt: \(f'(x) = 2e^{-x} \cdot \left( 1 - 4e^{-x} \right)\).
(3 BE)
Lösung zu Teilaufgabe 1a
Erste Ableitung bilden, Ableitungsregeln anwenden
\[f(x) = 2e^{-x} \cdot \left( 2e^{-x} - 1 \right); D_{f} = \mathbb R\]
Die Ableitungsfunktion \(f'\) von \(f\) lässt sich mit der Produktregel oder nach Umformung des Funktionsterms \(f(x)\) auch ohne die Produktregel formulieren. Zudem wird die Ableitung einer natürlichen Exponentialfunktion, die Kettenregel sowie die Summen- und die Faktorregel benötigt.
\[f(x) = 2e^{-x} \cdot \left( 2e^{-x} - 1 \right) = 4e^{-2x} - 2e^{-x}\]
Mit Produktregel:
\[f(x) = 2e^{-x} \cdot \left( 2e^{-x} - 1 \right)\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= 2e^{-x} \cdot (-1) \cdot \left( 2e^{-x} - 1 \right) + 2e^{-x} \cdot \left( 2e^{-x} \cdot (-1) - 0 \right) \\[0.8em] &= 2e^{-x} \cdot \left( -2e^{-x} + 1 \right) + 2e^{-x} \cdot \left( -2e^{-x} \right) & &| \; \text{Faktor}\;2e^{-x} \; \text{ausklammern} \\[0.8em] &= 2e^{-x} \cdot \left( -2e^{-x} + 1 - 2e^{-x} \right) \\[0.8em] &= 2e^{-x} \cdot \left( 1 - 4e^{-x} \right) \end{align*}\]
Ohne Produktregel:
\[f(x) = 4e^{-2x} - 2e^{-x}\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= 4e^{-2x} \cdot (-2) - 2e^{-x} \cdot (-1) \\[0.8em] &= -8e^{-2x} + 2e^{-x} & &| \; \text{Faktor}\;2e^{-x} \; \text{ausklammern} \\[0.8em] &= 2e^{-x} \cdot \left( 1 - 4e^{-x} \right) \end{align*}\]

