Bestimmen Sie rechnerisch eine Gleichung der Tangente \(t\) an \(G_{f}\) im Punkt \((3|f(3))\). Berechnen Sie die Größe des Winkels, unter dem \(t\) die \(x\)-Achse schneidet, und zeichnen Sie \(t\) in die Abbildung 1 ein.
(4 BE)
Teilaufgabe 1c
Lösung zu Teilaufgabe 1c
\[f(x) = \frac{x^{2} - 1}{x^{2} + 1}; \; D_{f} = \mathbb R\]
\(f'(x) = \dfrac{4x}{(x^{2} + 1)^{2}}\) (vgl. Teilaufgabe 1b)
Gleichung der Tangente \(t\)
Zunächst wird die \(y\)-Koordinate des Punktes \((3|f(3))\) berechnet:
\[f(3) = \frac{3^{2} - 1}{3^{2} + 1} = \frac{8}{10} = 0{,}8\]
\[\Longrightarrow \quad (3|0{,}8)\]
Der Ansatz für die Gleichung der Tangente \(t\) kann mit der allgemeinen Geradengleichung erfolgen.
\[t \colon y = mx + c\]
Tangentensteigung berechnen:
Die erste Ableitung \(f'\) beschreibt die Steigung einer Tangente an den Graphen von \(f\).
\[m = f'(3) = \frac{4 \cdot 3}{(3^{2} + 1)^{2}} = \frac{12}{100} = 0{,}12\]
\[\Longrightarrow \quad t \colon y = 0{,}12x + c\]
\(y\)-Achsenabschnitt \(c\) berechnen:
Hierfür werden die Koordinaten des Punktes \((3|0{,}8)\) in die Gleichung der Tangente \(t\) eingesetzt und diese nach \(c\) aufgelöst.
\[\begin{align*} (3|0{,}8) \in t \colon 0{,}8 &= 0{,}12 \cdot 3 + c \\[0.8em] 0{,}8 &= 0{,}36 + c &&| -0{,}36 \\[0.8em] 0{,}44 &= c \end{align*}\]
\[\Longrightarrow \quad t \colon y = 0{,}12x + 0{,}44\]
Größe des Winkels, unter dem \(t\) die \(x\)-Achse schneidet
Im Falle der positiven Steigung \(m = 0{,}12\) der Tangente \(t\) entspricht der spitze Winkel, unter dem \(t\) die \(x\)-Achse schneidet, dem Steigungswinkel \(\alpha\) der Tangente \(t\).
\[\begin{align*} \tan{\alpha} &= m \\[0.8em] \tan{\alpha} &= 0{,}12 &&| \; \text{TR:}\; \tan^{-1}(0{,}12) \\[1.6em] \Rightarrow \alpha &\approx 6{,}84^{\circ} \end{align*}\]
Einzeichnen der Tangente \(t\) in Abbildung 1
Es ist ungünstig, für die Steigung \(m = 0{,}12 = \frac{12}{100}\) ein Steigungsdreieck zu zeichnen. Deshalb empfiehlt es sich, für das Einzeichnen der Tangente \(t\) die beiden bekannten Punkte \((3|0{,}8)\) und \((0|0{,}44)\) (vgl. \(y\)-Achsenabschnitt von \(t\)) zu verwenden.
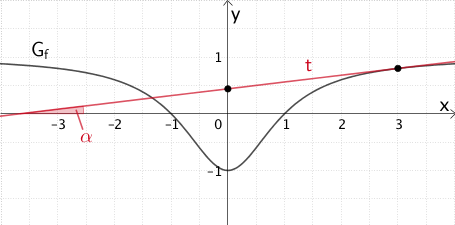
Tangente \(t\) an den Graphen der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \dfrac{x^{2} - 1}{x^{2} + 1}\) mit Winkel \(\alpha\), unter dem die Tangente die \(x\)-Achse schneidet.
