Die Abbildung 2 zeigt den Grundriss des Hallenmodells in der \(x_{1}x_{2}\)-Ebene. Stellen Sie unter Verwendung der bisherigen Ergebnisse den Schattenbereich der Flutlichtanlage in der Abbildung exakt dar.
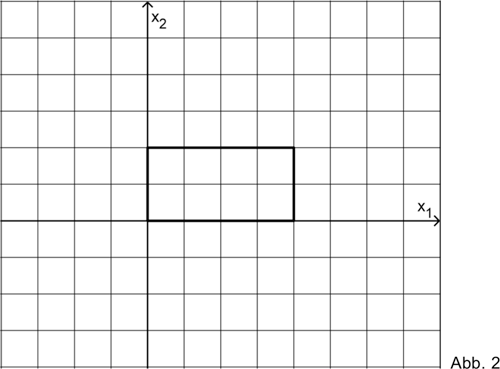
(4 BE)
Lösung zu Teilaufgabe f
Mithilfe der aus Teilaufgabe e bekannten Gleichung der Schnittgerade \(g\) der Ebene \(F\) und der \(x_{1}x_{2}\)-Ebene (vgl. Kontrollergebnis) sowie unter Berücksichtigung der Lage der Lichtquelle \(L\) (vgl. Teilaufgabe d) lässt sich der Schattenbereich der Flutlichtanlage exakt darstellen.
![Schattenlinie [S₂S₃] der Dachkante [B₂B₃], Schnittpunkt S₂ der Schnittgerade g mit der x₁-Achse](/images/stories/B2020_PT_B_G1/B2020_PT_B_G1_f10.png)
Da die Ebene \(\textcolor{#0087c1}{F}\) die Punkte \(\textcolor{#e9b509}{L}\) (Lichtquelle), \(B_{2}\) und \(B_{3}\) (Dachpunkte) enthält (vgl. Teilaufgabe d), liegt die Schattenlinie \([S_{2}S_{3}]\) der Dachkante \([B_{2}B_{3}]\) auf der Schnittgeraden \(\textcolor{#cc071e}{g}\) der Ebene \(\textcolor{#0087c1}{F}\) und der \(x_{1}x_{2}\)-Ebene (vgl. Teilaufgabe e).
Die Punkte \(L(10|\textcolor{#89ba17}{0}|12)\) und \(B_{2}(20|\textcolor{#89ba17}{0}|6)\) liegen in der \(\textcolor{#89ba17}{x_{1}x_{3}}\)-Ebene. Deshalb liegt der Schattenpunkt \(S_{2}\) des Dachpunktes \(B_{2}\) sowohl in der \(x_{1}x_{3}\)-Ebene als auch in der \(x_{1}x_{2}\)-Ebene (Projektionsebene) und damit auf der \(x_{1}\)-Achse. Der Schattenpunkt \(S_{2}\) ist der Schnittpunkt von \(\textcolor{#cc071e}{g}\) mit der \(x_{1}\)-Achse.
Koordinaten des Schattenpunktes \(S_{2}\) des Dachpunktes \(B_{2}\)
Aus Teilaufgabe 1e ist die Gleichung der Schnittgeraden \(g\) der Ebene \(F\) und der \(x_{1}x_{2}\)-Ebene bekannt.
\[g \colon \overrightarrow{X} = \textcolor{#89ba17}{\begin{pmatrix} 30 \\ 0 \\ 0 \end{pmatrix}} + \lambda \cdot \begin{pmatrix} 1 \\ -3 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\]
Die Geradengleichung verwendet den Aufpunkt \(\textcolor{#89ba17}{(30|0|0)}\). Die \(x_{2}\)- und die \(x_{3}\)-Koordinate des Aufpunkts haben den Wert Null. Deshalb liegt der Punkt auf der \(\textcolor{#89ba17}{x_{1}}\)-Achse. Der Aufpunkt von \(g\) ist somit der Schattenpunkt \(\textcolor{#89ba17}{S_{2}}\) des Dachpunktes \(B_{2}\).
\[\textcolor{#89ba17}{S_{2}(30|0|0)}\]
Schnittgerade \(g\) in Abbildung 2 einzeichnen
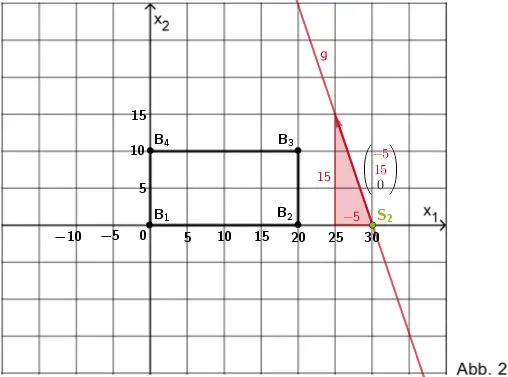
Abbildung 2 zeigt die Aufsicht auf die \(x_{1}x_{2}\)-Ebene. Das abgebildete Rechteck stellt die Dachfläche der Mehrzweckhalle dar. Da die Mehrzweckhalle 20 m lang ist (vgl. Angabe) entspricht die Seitenlänge eines Kästchens 5 LE (Längeneinheiten).
Bei dieser Skalierung ist es schwierig, die Schnittgerade \(\textcolor{#cc071e}{g}\) mithilfe deren Richtungsvektor \(\begin{pmatrix} 1 \\ -3 \\ 0 \end{pmatrix}\) exakt einzuzeichnen. Es empfiehlt sich, ein geeignetes Vielfaches des Richtungsvektors zu verwenden.
Beispielsweise ist \((-5) \cdot \begin{pmatrix} 1 \\ -3 \\ 0 \end{pmatrix} = \begin{pmatrix} \textcolor{#cc071e}{-5} \\ \textcolor{#cc071e}{15} \\ 0 \end{pmatrix}\) ebenfalls ein Richtungsvektor von \(\textcolor{#cc071e}{g}\).
Schattenpunkt \(S_{3}\) des Dachpunktes \(B_{3}\) ermitteln
![Lichtstrahl durch Dachpunkt B₃, Schattenpunkt S₃ auf der Schnittgeraden g, Scahattenlinie [S₂S₃] der Dachkante [B₂B₃]](/images/stories/B2020_PT_B_G1/B2020_PT_B_G1_f7.png)
Ein von der Lichtquelle \(\textcolor{#e9b509}{L(10|0|12)}\) ausgehender Lichtstrahl projiziert den Schattenpunkt \(S_{3}\) des Dachpunktes \(B_{3}\) in die \(x_{1}x_{2}\)-Ebene. Da die Ebene \(F\) den Dachpunkt \(B_{3}\) enthält, liegt der Schattenpunkt \(S_{3}\) auf der Schnittgeraden \(\textcolor{#cc071e}{g}\) der Ebene \(F\) und der \(x_{1}x_{2}\)-Ebene.
Schattenlinie \([S_{2}S_{3}]\) der Dachkante \([B_{2}B_{3}]\) spiegeln
![Schattenlinie [S₂S₃] gespiegelt an der Ebene x₁ = 10](/images/stories/B2020_PT_B_G1/B2020_PT_B_G1_f8.png)
Weil die Lichtquelle \(\textcolor{#e9b509}{L(10|0|12)}\) vertikal über dem Mittelpunkt der Kante \([A_{1}A_{2}]\) liegt (vgl. Angabe), ist der Schattenbereich symmetrisch zur Ebene mit der Gleichung \(x_{1} = 10\). Durch Spiegelung der Schattenlinie \([S_{2}S_{3}]\) an dieser Ebene ergibt sich die Schattenlinie \([S_{1}S_{4}]\) der Dachkante \([B_{1}B_{4}]\). In der Aufsicht auf die \(x_{1}x_{2}\)-Ebene von Abbildung 2 erscheint die Symmetrieebene als Gerade (gestrichelt gezeichnet).
Schattenbereich der Flutlichtanlage vervollständigen
![Schattenlinie [S₃S₄] der Dachkante [B₃B₄], Schattenbereich der Flutlichtanlage](/images/stories/B2020_PT_B_G1/B2020_PT_B_G1_f9.png)
Das Einzeichnen der Schattenlinie \([S_{3}S_{4}]\) der Dachkante \([B_{3}B_{4}]\) vervollständigt den Schattenbereich der Flutlichtanlage.
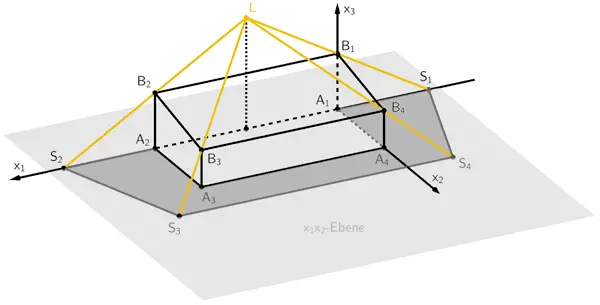
Schattenbereich der Flutlichtanlage (Zeichnung nicht verlangt)
Rechnerische Bestimmung der Koordinaten des Schattenpunktes \(S_{3}\) des Dachpunktes \(B_{3}\) (nicht verlangt)
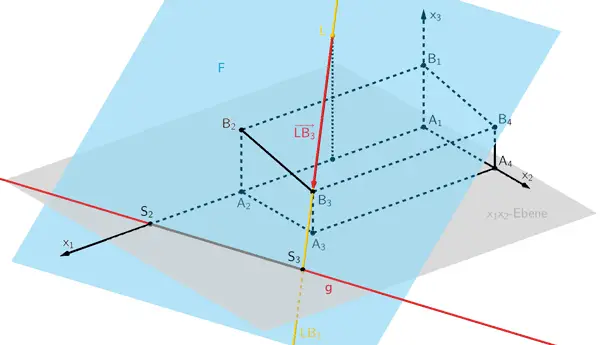
Beispielsweise liefert der Punkt \(\textcolor{#e9b509}{L(10|0|12)}\) und der Verbindungsvektor \(\textcolor{#cc071e}{\overrightarrow{LB_{3}} = \begin{pmatrix} 10 \\ 10 \\ -8 \end{pmatrix}}\) (vgl. Teilaufgabe d) eine Gleichung der Geraden \(\textcolor{#e9b509}{LB_{3}}\) in Parameterform.
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} \textcolor{#e9b509}{LB_{3}} \colon \overrightarrow{X} &= \textcolor{#e9b509}{\overrightarrow{L}} + \mu \cdot \textcolor{#cc071e}{\overrightarrow{LB_{3}}}; \; \mu \in \mathbb R \\[0.8em] \textcolor{#e9b509}{LB_{3}} \colon \overrightarrow{X} &= \textcolor{#e9b509}{\begin{pmatrix} 10 \\ 0 \\ 12 \end{pmatrix}} + \mu \cdot \textcolor{#cc071e}{\begin{pmatrix} 10 \\ 10 \\ -8 \end{pmatrix}}; \; \mu \in \mathbb R \end{align*}\]
Schnittpunkt \(S_{3}\) der Geraden \(LB_{3}\) mit der \(x_{1}x_{2}\)-Ebene berechnen:
Hierfür wird die \(x_{3}\)-Koordinate des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Geraden \(LB_{3}\) in die Gleichung \(x_{3} = 0\) der \(x_{1}x_{2}\)-Ebene eingesetzt und die Gleichung nach dem Parameter \(mu\) aufgelöst.
\[LB_{3} \colon \overrightarrow{X} = \begin{pmatrix} 10 \\ 0 \\ \textcolor{#89ba17}{12} \end{pmatrix} + \textcolor{#89ba17}{\mu} \cdot \begin{pmatrix} 10 \\ 10 \\ \textcolor{#89ba17}{-8} \end{pmatrix}; \; \mu \in \mathbb R\]
\[x_{1}x_{2}\text{-Ebene}\colon x_{3} = 0\]
\[\begin{align*}LB_{3} \cap x_{1}x_{2}\text{-Ebene}\colon \textcolor{#89ba17}{12 - 8\mu} &= 0 &&| + 8\mu \\[0.8em] 12 &= 8\mu &&| : 8 \\[0.8em] \mu &= \frac{12}{8} \\[0.8em] &= 1{,}5\end{align*}\]
Einsetzen des Parameterwerts \(\textcolor{#89ba17}{\mu = 1{,}5}\) in die Gleichung der Geraden \(LB_{3}\) ergibt den Ortsvektor \(\overrightarrow{S_{3}}\) des Punktes \(S_{3}\).
\[S_{3} \in LB_{3} \colon \overrightarrow{S_{3}} = \begin{pmatrix} 10 \\ 0 \\ 12 \end{pmatrix} + \textcolor{#89ba17}{1{,}5} \cdot \begin{pmatrix} 10 \\ 10 \\ -8 \end{pmatrix} = \begin{pmatrix} 25 \\ 15 \\ 0 \end{pmatrix}\]
\[\Rightarrow \enspace S_{3}(25|15|0)\]

