Berechnen Sie die Größe des Schnittwinkels von \(g\) und \(E\) und zeigen Sie, dass \(S(0{,}5|6{,}5|0)\) der Schnittpunkt von \(g\) und \(E\) ist.
(5 BE)
Lösung zu Teilaufgabe b
Berechnung der Größe des Schnittwinkel von \(g\) und \(E\)
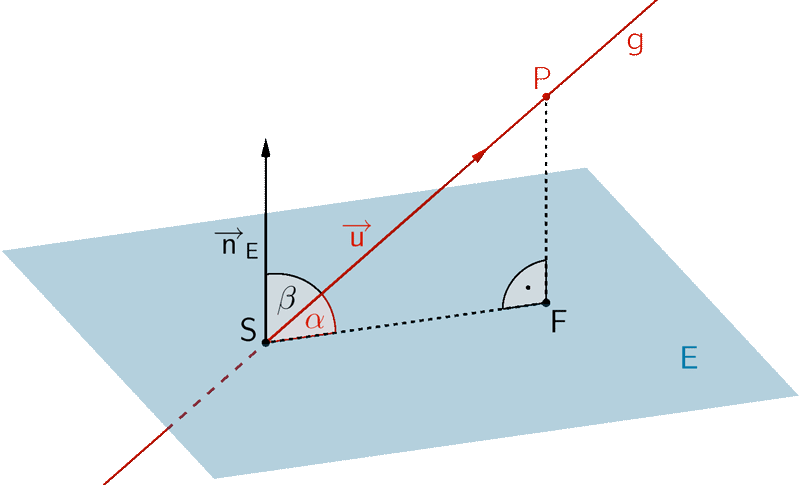
Schnittwinkel \(\boldsymbol{\alpha}\) zwischen Gerade und Ebene
Für \(0^{\circ} \leq \alpha \leq 90^{\circ}\) und \(0^{\circ} \leq \beta \leq 90^{\circ}\) gilt:
\[\begin{align*} \cos \beta &= \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \enspace \Rightarrow \enspace \beta = \cos^{-1}(\dots) \\[0.8em] \alpha &= 90^{\circ} - \beta \end{align*}\]
\[\sin \alpha = \frac{\vert \overrightarrow{u} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \enspace \Rightarrow \enspace \alpha = \sin^{-1}(\dots)\]
\[E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{\overrightarrow{n}_{E} = \begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix}}\]
\[g \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \textcolor{#e9b509}{\begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}}, \; \lambda \in \mathbb R\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \sin \alpha &= \frac{\vert \textcolor{#e9b509}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}_{E}} \vert}{\vert \textcolor{#e9b509}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}_{E}} \vert} = \frac{\left|\textcolor{#e9b509}{\begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}} \circ \textcolor{#0087c1}{\begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix}}\right|}{\left| \textcolor{#e9b509}{\begin {pmatrix} 5 \\ 11 \\ -4 \end {pmatrix}} \right| \cdot \left| \textcolor{#0087c1}{\begin {pmatrix} 4 \\ -8 \\ 1 \end {pmatrix}} \right|} \\[0.8em] &= \frac{\vert 5 \cdot 4 + 11 \cdot (-8) + (-4) \cdot 1\vert}{\sqrt{5^2 + 11^2 + (-4)^2} \cdot \sqrt{4^2 + (-8)^2 + 1^2}} \\[0.8em] &= \frac{\vert -72 \vert}{\sqrt{81} \cdot \sqrt{162}} = \frac{72}{9 \cdot \sqrt{162}} = \frac{8}{\sqrt{162}} & &| \; \text{TR}\colon\, \sin^{-1}(\dots) \\[2.4em] \alpha &= \sin^{-1}\left( \frac{8}{\sqrt{162}} \right) \approx 38{,}9^{\circ} \end{align*}\]
Die Gerade \(g\) schneidet die Ebene \(E\) unter einem Winkel von ca. 38,9°.
Nachweis, dass \(S(0{,}5|6{,}5|0)\) der Schnittpunkt von \(g\) und \(E\) ist
1. Möglichkeit: Punktprobe
\[\textcolor{#89ba17}{S(0{,}5|6{,}5|0)}\]
\[g \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}, \; \lambda \in \mathbb R\]
\[\textcolor{#89ba17}{S} \;\text{in}\; g\colon \; \textcolor{#89ba17}{\begin{pmatrix} 0{,}5 \\ 6{,}5 \\ 0 \end{pmatrix}} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}\]
\[\Rightarrow \enspace \left\{ \begin{align*} 0{,}5 = \enspace 3 + \enspace 5 \lambda \enspace &\Leftrightarrow \enspace \lambda = -0{,}5 \\[0.8em] 6{,}5 = 12 + 11\lambda \enspace &\Leftrightarrow \enspace \lambda = -0{,}5 \\[0.8em] \enspace 0 = -2 - \enspace 4\lambda \enspace &\Leftrightarrow \enspace \lambda = -0{,}5\end{align*} \right\} \enspace \Rightarrow \enspace \textcolor{#89ba17}{S} \in g\]
\[\textcolor{#89ba17}{S(0{,}5|6{,}5|0)}\]
\[E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0\]
\[\begin{align*}\textcolor{#89ba17}{S}\; \text{in}\; E \colon \; 4 \cdot \textcolor{#89ba17}{0{,}5} - 8 \cdot \textcolor{#89ba17}{6{,}5} + \textcolor{#89ba17}{0} + 50 &= 0 \\[0.8em] 2 - 52 +50 &= 0 \\[0.8em] -50 + 50 &= 0 \quad \text{(w)} \end{align*}\]
\[\Rightarrow \enspace \textcolor{#89ba17}{S} \in E\]
\[\Rightarrow \enspace \textcolor{#89ba17}{S} \in g, E\]
Also ist \(\textcolor{#89ba17}{S(0{,}5|6{,}5|0)}\) der Schnittpunkt von \(g\) und \(E\).
2. Möglichkeit: Koordinaten des Schnittpunkts bestimmen
\[\begin{align*}g \colon \overrightarrow{X} &= \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}, \; \lambda \in \mathbb R \\[0.8em] g \colon \overrightarrow{X} &= \begin{pmatrix} \textcolor{#0087c1}{3 + 5\lambda} \\ \textcolor{#e9b509}{12 + 11\lambda} \\ \textcolor{#cc071e}{-2 - 4\lambda} \end{pmatrix}, \; \lambda \in \mathbb R \end{align*}\]
\[E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0\]
Für die Berechnung der Koordinaten des Schnittpunkts von \(g\) und \(E\) werden die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Geraden \(g\) in die Gleichung der Ebene \(E\) eingesetzt und diese nach dem Parameter \(\lambda\) aufgelöst.
\[\begin{align*} g \cap E \colon \; 4 \cdot \textcolor{#0087c1}{(3 + 5\lambda)} - 8 \cdot \textcolor{#e9b509}{(12 + 11\lambda)} + \textcolor{#cc071e}{(-2 - 4\lambda)} + 50 &= 0 \\[0.8em] 12 + 20 \lambda - 96 - 88 \lambda - 2 - 4 \lambda + 50 &= 0 \\[0.8em] -72\lambda - 36 &= 0 &&| + 36 \\[0.8em] -72 &= 36 &&| : (-72) \\[0.8em] \lambda &= -0{,}5 \end{align*}\]
Eingesetzt in die Geradengleichung von \(g\) liefert der Parameterwert \(\textcolor{#89ba17}{\lambda = -0{,}5}\) den Ortsvektor \(\overrightarrow{S}\) des Schnittpunkts \(S\) von \(g\) und \(E\).
\[S \in g \colon \;\overrightarrow{S} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \textcolor{#89ba17}{(-0{,}5)} \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix} = \begin{pmatrix} 0{,}5 \\ 6{,}5 \\ 0 \end{pmatrix}\]
\[\Rightarrow \enspace S(0{,}5|6{,}5|0)\]

