Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Wertemenge \(W\) hat.
\[W =\; ]3;+\infty[\]
(2 BE)
Lösung zu Teilaufgabe 2b
zum Beispiel: \(e^{x} + 3\)
Begründung (nicht verlangt)
Der Graph der Funktion \(x \mapsto e^{x} \textcolor{#cc071e}{+ 3}\) ist gegenüber dem Graphen der natürlichen Exponentialfunktion \(x \mapsto e^{x}\) um + 3 LE (Längeneinheiten) in y-Richtung verschoben und besitzt deshalb für \(x \to -\infty\) die waagrechte Asymptote mit der Gleichung \(\textcolor{#cc071e}{y = 3}\).
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Rightarrow \enspace W = \; \textcolor{#cc071e}{]3};+\infty[\]
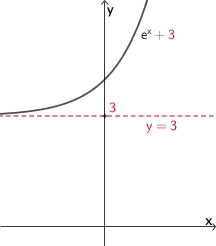 Skizze nicht verlangt
Skizze nicht verlangt
Anmerkung:
Für die Bearbeitung derartiger Aufgaben ist die Kenntnis über den Verlauf der Graphen von Grundfunktionen sehr hilfreich.
(vgl. Abiturskript - Lernhilfen Analysis - Skizzieren des Verlaufs wichtiger Grundfunktionen)

