Gegeben ist die Zufallsgröße \(X\) mit der Wertemenge \(\{0;1;2;3;4;5\}\). Die Wahrscheinlichkeitsverteilung von \(X\) ist symmetrisch, d. h. es gilt \(P(X = 0) = P(X = 5)\), \(P(X = 1) = P(X = 4)\), \(P(X = 2) = P(X = 3)\).
Die Tabelle zeigt die Wahrscheinlichkeitswerte \(P(X \leq k)\) für \(k \in \{0; 1; 2\}\).

Tragen Sie die fehlenden Werte in die Tabelle ein.
(2 BE)
Lösung zu Teilaufgabe a
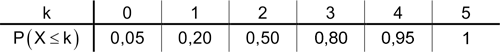
Begründung (nicht verlangt)

Die Tabelle zeigt die aufsummierten Wahrscheinlichkeitswerte \(P(X \textcolor{#cc071e}{\leq} k) = P(X = 0) \textcolor{#cc071e}{+} \dots \textcolor{#cc071e}{+} P(X = k)\) (kumulative Verteilungsfunktion), d. h. die Wahrscheinlichkeit dafür, dass die Zufallsgröße höchstens einen Wert \(k\) annimmt.
Eine mögliche Vorgehensweise veranschaulicht die nachfolgende, um die Wahrscheinlichkeitswerte \(\textcolor{#e9b509}{P(X = k)}\) ergänzte Tabelle.

Es gilt:
\[\begin{align*}P(X \textcolor{#cc071e}{\leq} 1) &= P(X = 0) \textcolor{#cc071e}{+} P(X = 1) &&| - P(X = 0) \\[0.8em] P(X \leq 1) - P(X = 0) &= P(X = 1) \\[0.8em] 0{,}20 - 0{,}05 &= P(X = 1) \\[0.8em] \textcolor{#e9b509}{0{,}15} &\textcolor{#e9b509}{=} \textcolor{#e9b509}{P(X = 1)} \end{align*}\]
\[\begin{align*}P(X \textcolor{#cc071e}{\leq} 2) &= \underbrace{P(X = 0) \textcolor{#cc071e}{+} P(X = 1)}_{\Large{P(X\, \textcolor{#cc071e}{\leq}\, 1})} \textcolor{#cc071e}{+} P(X = 2) \\[0.8em] P(X \leq 2) &= P(X \leq 1) \textcolor{#cc071e}{+} P(X = 2) &&| - P(X \leq 1) \\[0.8em] P(X \leq 2) - P(X \leq 1) &= P(X = 2) \\[0.8em] 0{,}50 - 0{,}20 &= P(X = 1) \\[0.8em] \textcolor{#e9b509}{0{,}30} &\textcolor{#e9b509}{=} \textcolor{#e9b509}{P(X = 2)} \end{align*}\]
Da die Wahrscheinlichkeitsverteilung von \(X\) symmetrisch ist (vgl. Angabe), gilt:
\(\textcolor{#e9b509}{P(X = 0) = P(X = 5) = 0{,}05}\),
\(\textcolor{#e9b509}{P(X = 1) = P(X = 4) = 0{,}15}\) und
\(\textcolor{#e9b509}{P(X = 2) = P(X = 3) = 0{,}30}\).
Damit ergibt sich:
\[\begin{align*} P(X \textcolor{#cc071e}{\leq} 3) &= P(X \textcolor{#cc071e}{\leq} 2) \textcolor{#e9b509}{+ P(X = 3)} \\[0.8em] &= 0{,}50 \textcolor{#e9b509}{+ 0{,}30} \\[0.8em] &= 0{,}80 \end{align*}\]
\[\begin{align*} P(X \textcolor{#cc071e}{\leq} 4) &= P(X \textcolor{#cc071e}{\leq} 3) \textcolor{#e9b509}{+ P(X = 4)} \\[0.8em] &= 0{,}80 \textcolor{#e9b509}{+ 0{,}15} \\[0.8em] &= 0{,}95 \end{align*}\]
\[\begin{align*} P(X \textcolor{#cc071e}{\leq} 5) &= P(X \textcolor{#cc071e}{\leq} 4) \textcolor{#e9b509}{+ P(X = 5)} \\[0.8em] &= 0{,}95 \textcolor{#e9b509}{+ 0{,}05} \\[0.8em] &= 1 \end{align*}\]

