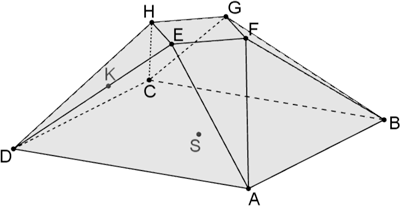
 Abb. 1
Abb. 1
Der in Abbildung 1 dargestellte Körper wird begrenzt von der quadratischen Grundfläche \(ABCD\) mit \(A(5|5|0)\), \(B(-5|5|0)\), \(C(-5|-5|0)\) und \(D(5|-5|0)\), acht dreieckigen Seitenflächen und einem weiteren Quadrat \(EFGH\) mit \(E(2|0|4)\), \(F(0|2|4)\), \(G(-2|0|4)\) und \(H(0|-2|4)\). Der Mittelpunkt \(S\) des Quadrats \(ABCD\) ist der Ursprung des Koordinatensystems und der gesamte Körper ist symmetrisch sowohl bezüglich der \(x_{1}x_{3}\)-Ebene als auch bezüglich der \(x_{2}x_{3}\)-Ebene.
Zeigen Sie, dass das Dreieck \(ABF\) bei \(F\) rechtwinklig ist.
(2 BE)
Lösung zu Teilaufgabe a
Das Dreieck \(ABF\) ist bei \(F\) rechtwinklig, wenn das Skalarprodukt der Verbindungsvektoren \(\overrightarrow{FA}\) und \(\overrightarrow{FB}\) gleich null ist.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{FA} \perp \overrightarrow{FB} \enspace \Leftrightarrow \enspace \overrightarrow{FA} \circ \overrightarrow{FB}\]
Verbindungsvektoren \(\overrightarrow{FA}\) und \(\overrightarrow{FB}\) bestimmen:
\(A(5|5|0)\), \(B(-5|5|0)\), \(F(0|2|4)\)
\[\overrightarrow{FA} = \overrightarrow{A} - \overrightarrow{F} = \begin{pmatrix} 5 \\ 5 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 2 \\ 4 \end{pmatrix} = \begin{pmatrix} 5 \\ 3 \\ -4 \end{pmatrix}\]
\[\overrightarrow{FB} = \overrightarrow{B} - \overrightarrow{F} = \begin{pmatrix} -5 \\ 5 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 2 \\ 4 \end{pmatrix} = \begin{pmatrix} -5 \\ 3 \\ -4 \end{pmatrix}\]
Skalarbrodukt von \(\overrightarrow{FA}\) und \(\overrightarrow{FB}\) berechnen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}\overrightarrow{FA} \circ \overrightarrow{FB} &=\begin{pmatrix} \textcolor{#e9b509}{5} \\ \textcolor{#0087c1}{3} \\ \textcolor{#cc071e}{-4} \end{pmatrix} \circ\begin{pmatrix} \textcolor{#e9b509}{-5} \\ \textcolor{#0087c1}{3} \\ \textcolor{#cc071e}{-4} \end{pmatrix} \\[0.8em] &= \textcolor{#e9b509}{5} \cdot \textcolor{#e9b509}{(-5)} + \textcolor{#0087c1}{3} \cdot \textcolor{#0087c1}{3} + \textcolor{#cc071e}{(-4)} \cdot \textcolor{#cc071e}{(-4)} \\[0.8em] &= -25 + 9 + 16 \\[0.8em] &= 0\end{align*}\]
Also ist das Dreieck \(ABF\) bei \(F\) rechtwinklig.

