Lösung zu Teilaufgabe 1f
\[F(x) = \int_{a}^{x} f(t)\,dt\,; \quad D = \mathbb R\]
Die Integralfunktion \(F\) hat an der unteren Integrationsbgrenze \(x = a\) eine Nullstelle.
Nullstelle einer Integralfunktion
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
\[F(a) = \int_{a}^{a} f(t)\,dt = 0\]
Aus Teilaufgabe 5b ist bekannt:
\[f(a) = 0\]
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F'(a) = f(a) = 0\]
\(\Longrightarrow \quad\) Der Punkt \((a|F(a))\) ist Extrempunkt der Integralfunktion \(F\).
Art des Extrempunkts:
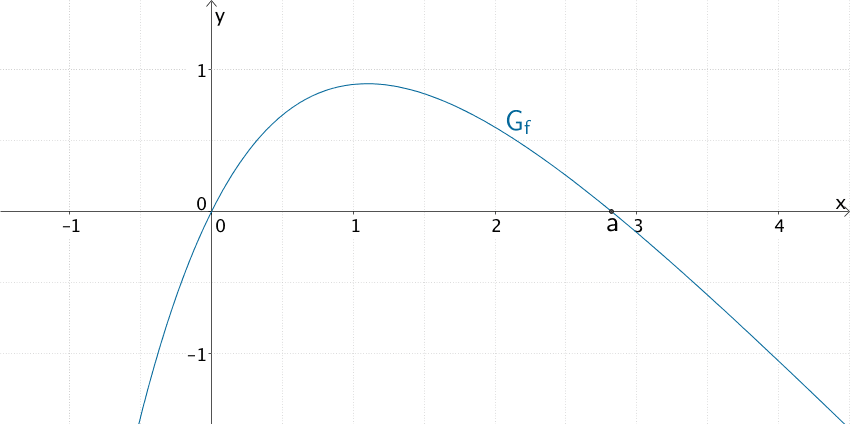
Ger Graph der Funktion \(f\) wechselt an der Nullstelle \(x = a\) das Vorzeichen von plus nach minus. Demnach verläuft der Graph der Integralfunktion \(F\) für \(x < a\) streng monoton steigend und für \(x > a\) streng monoton fallend. Folglich besitzt der Graph der Integralfunktion \(F\) an der Stelle \(x = a\) einen Hochpunkt.
Hauptsatz der Differential- und Integralrechnung
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F'(x) = f(x)\]
Monotoniekriterium
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \quad \Longrightarrow \quad G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \quad \Longrightarrow \quad G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*}&F'(x) > 0 \enspace \text{für} \enspace x < a \\ &F'(a) = 0 \\ &F'(x) < 0 \enspace \text{für} \enspace x > a \end{align*} \right \} \enspace \Rightarrow \enspace \text{Hochpunkt}\;(a|F(a))\]
Fazit: Der Graph der Integralfunktion \(F\) hat im Punkt \((a|F(a))\) einen Hochpunkt und berührt in diesem die \(x\)-Achse.
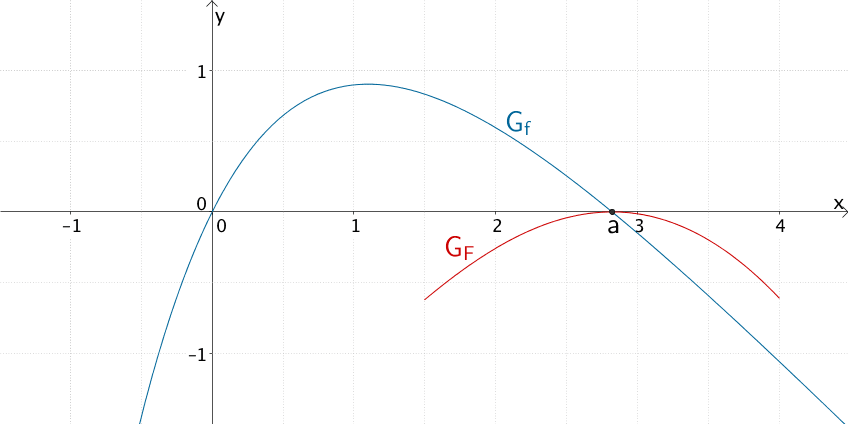
Verlauf des Graphen der Intergralfunktion \(F\) in der Umgebung der Stelle \(x = a\)
