- Details
- Kategorie: Analysis I - Teil 2
Gegeben ist die Funktion \(f \colon x \mapsto \displaystyle \frac{2e^x}{e^x + 9}\) mit Definitionsbereich \(\mathbb R\). Abbildung 2 zeigt den Graphen \(G_f\) von \(f\,\).
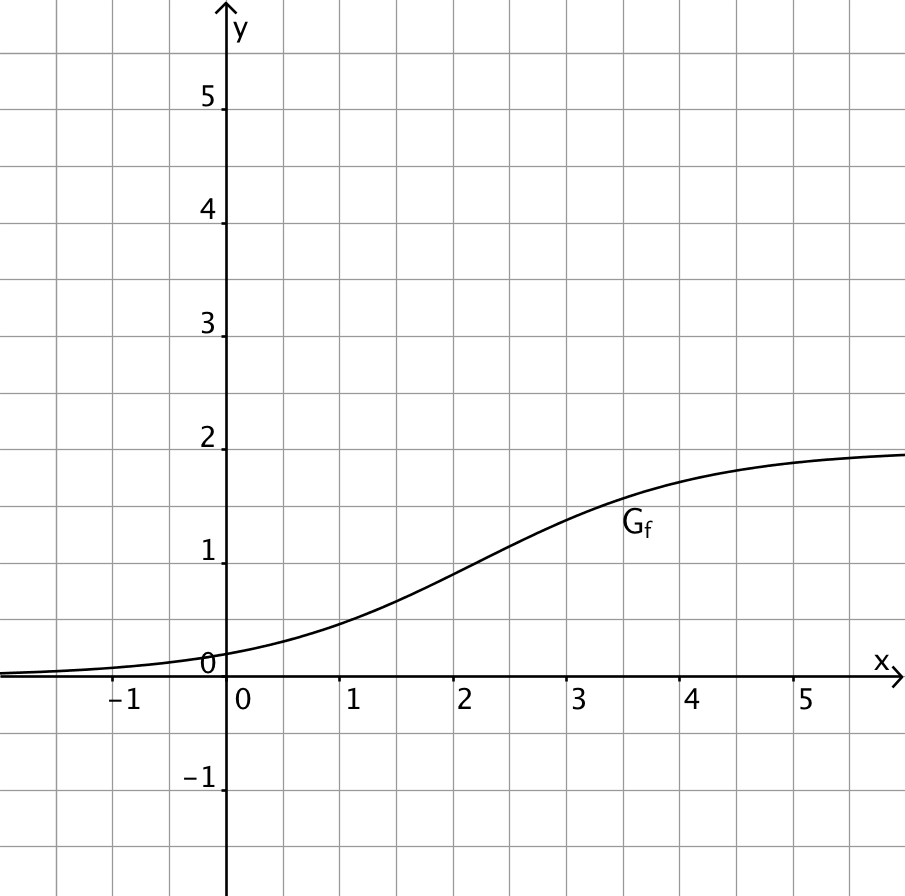 Abb. 2
Abb. 2
Zeigen Sie rechnerisch, dass \(G_f\) genau einen Achsenschnittpunkt \(S\) besitzt, und geben Sie die Koordinaten von \(S\) an.
(2 BE)
- Details
- Kategorie: Analysis I - Teil 2
Begründen Sie mithilfe des Funktionsterms von \(f\), dass \(\lim \limits_{x \, \to \, -\infty} f(x) = 0\) und \(\lim \limits_{x \, \to \, +\infty} f(x) = 2\) gilt.
(2 BE)
- Details
- Kategorie: Analysis I - Teil 2
Weisen Sie rechnerisch nach, dass \(G_f\) in \(\mathbb R\) streng monoton steigt.
(zur Kontrolle: \(f'(x)= \displaystyle \frac{18e^x}{(e^x + 9)^2}\))
(3 BE)
- Details
- Kategorie: Analysis I - Teil 2
Bestimmen Sie die Gleichung der Tangente an \(G_f\) im Achsenschnittpunkt \(S\).
(Ergebnis: \(y = 0{,}18x + 0{,}2\))
(2 BE)
- Details
- Kategorie: Analysis I - Teil 2
Berechnen Sie den Inhalt der Fläche, die \(G_f\) mit den Koordinatenachsen und der Geraden \(x = 4\) einschließt.
(4 BE)
- Details
- Kategorie: Analysis I - Teil 2
Begründen Sie, dass \(f\) in \(\mathbb R\) umkehrbar ist. Geben Sie den Definitionsbereich und den Wertebereich der Umkehrfunktion \(f^{-1}\) an und zeichnen Sie den Graphen von \(f^{-1}\) in Abbildung 2 ein.
(6 BE)
- Details
- Kategorie: Analysis I - Teil 2
Das Wachstum von Sonnenblumen der Sorte Alba lässt sich modellhaft mithilfe der Funktion \(f\) beschreiben. Beginnt man die Beobachtung zwei Wochen nach der Auskeimung einer Sonnenblume dieser Sorte, so liefert \(f(x)\) für \(x \in [0;4]\) im Modell die Höhe der Blume in Metern. Dabei ist \(x\) die seit Beobachtungsbeginn vergangene Zeit in Monaten. In den Aufgaben 2a bis 2d werden auschließlich Sonnenblumen der Sorte Alba betrachtet.
Berechnen Sie auf der Grundlage des Modells, um wie viele Zentimeter eine Sonnenblume innerhalb der ersten zwei Monate nach Beobachtungsbeginn wächst.
(2 BE)
- Details
- Kategorie: Analysis I - Teil 2
Berechnen Sie auf der Grundlage des Modells, wie viele Monate nach Beobachtungsbeginn eine Sonnenblume eine Höhe von 1,5 Metern erreicht. Beschreiben Sie, wie man den Wert graphisch überprüfen kann.
(5 BE)
- Details
- Kategorie: Analysis I - Teil 2
Im Modell gibt es einen Zeitpunkt \(x_M\), zu dem die Blumen am schnellsten wachsen. Bestimmen Sie mithilfe von Abbildung 2 einen Näherungswert für \(x_M\). Ermitteln Sie anschließend einen Näherungswert für die maximale Wachstumsrate in Zentimetern pro Tag.
(5 BE)
- Details
- Kategorie: Analysis I - Teil 2
Ein Biologe nimmt an, dass sich das Wachstum der Blumen vor Beobachtungsbeginn näherungsweise durch die Gleichung der Tangente aus Aufgabe 1d beschreiben lässt. Untersuchen Sie mithilfe einer Rechnung, ob diese Annahme damit in Einklang steht, dass vom Zeitpunkt des Auskeimens bis zum Beobachtungsbeginn etwa zwei Wochen vergehen.
(4 BE)
- Details
- Kategorie: Analysis I - Teil 2
Haben zu Beobachtungsbeginn Sonnenblumen der Sorte Tramonto die gleiche Höhe wie Sonnenblumen der Sorte Alba, so erreichen von da an die Sonnenblumen der Sorte Tramonto im Vergleich zu denen der Sorte Alba jede Höhe in der Hälfte der Zeit.
Das Wachstum von Sonnenblumen der Sorte Tramonto lässt sich modellhaft mithilfe einer in \(\mathbb R\) definierten Funktion \(g\) beschreiben, die eine Funktionsgleichung der Form I, II, oder III mit \(k \in \mathbb R^+\) besitzt:
\[\textsf{I}\enspace y = \frac{2e^{x+k}}{e^{x+k}+9}\]
\[\textsf{II}\enspace y = k \cdot \frac{2e^x}{e^x + 9}\]
\[\textsf{III}\enspace y = \frac{2e^{kx}}{e^{kx} + 9}\]
Dabei ist \(x\) die seit Beobachtungsbeginn vergangene Zeit in Monaten und \(y\) ein Näherungswert für die Höhe einer Blume in Metern.
Begründen Sie, dass weder eine Gleichung der Form I noch eine der Form II als Funktionsgleichung von \(g\) infrage kommt.
(4 BE)
- Details
- Kategorie: Analysis I - Teil 2
Die Funktionsgleichung von \(g\) hat also die Form III. Geben Sie den passenden Wert von \(k\) an.
(1 BE)

