An einer Wand im Innenhof der von Antoni Gaudi gestalteten Casa Battló in Barcelona findet man ein Keramikkunstwerk (vgl. Abbildung 1).
Der annähernd parabelförmige obere Rand des Kunstwerks soll durch den Graphen einer ganzrationalen Funktion modellhaft dargestellt werden. Auf dem Graphen sollen bei Verwendung des eingezeichneten Koordiantensystems die Punkte \(A\,(-2|0)\), \(B\,(2|0)\) und \(C\,(0|5)\) liegen (1 LE entspricht 1m, d.h. das Kunstwerk ist 5m hoch).
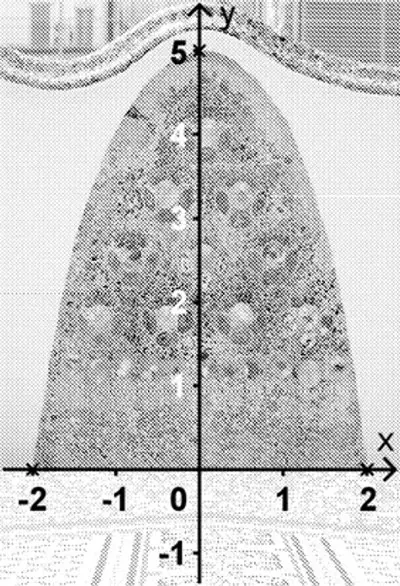 Abb. 1
Abb. 1
Ermitteln Sie den Term einer in \(\mathbb R\) definierten quadratischen Funktion \(p\), deren Graph durch die Punkte \(A\), \(B\) und \(C\) verläuft.
(zur Kontrolle: \(p(x) = -1{,}25x^2 + 5\))
(3 BE)
Lösung zu Teilaufgabe 1a
\[A\,(-2|0)\,, \quad B\,(2|0)\,, \quad C\,(0|5)\]
1. Lösungsansatz: Scheitelpunktform
Quadratische Funktion:
\[f(x) = ax^2 + bx + c\,; \quad a, b, c \, \in \, \mathbb R\,, a \neq 0\]
Scheitelpunktform
\[f(x) = a(x - d)^2 + e\]
Scheitelpunkt
\[S\,(d|e) \qquad d = -\frac{b}{2a}\,; \quad e = c - \frac{b^2}{4a}\]
Der Punkt \(C\,\) bescreibt den Scheitelpunkt der Parabel.
\[\begin{align*} p(x) &= a(x - x_C)^2 + y_C \\[0.8em] &= a(x - 0) + 5 \\[0.8em] &= ax^2 + 5 \end{align*}\]
\[\begin{align*} A \in p\, \colon \enspace 0 &= a \cdot (-2)^2 + 5 \\[0.8em] 0 &= 4a + 5 & &| -5 \\[0.8em] -5 &= 4a & &| :4 \\[0.8em] a &= -1{,}25 \end{align*}\]
\[\Longrightarrow \quad p(x) = -1{,}25x^2 + 5 \,; \quad D_p = \mathbb R\]
2. Lösungsansatz: Allgemeine Form
\[p(x) = ax^2 + bx + c\]
Lineares Gleichungssystem aufstellen:
\[A\,, \, B\,, \, C \, \in p\]
\[\begin{align*}\text{I} & & 0 &= a \cdot (-2)^2 + b \cdot (-2) + c \\[0.8em] \text{II} & & \wedge \quad 0 &= a \cdot 2^2 + b \cdot 2 + c \\[0.8em] \text{III} & & \wedge \quad 5 &= a \cdot 0^2 + b \cdot 0 + c \\[2.4em] \text{I} & & 0 &= 4a - 2b + c \\[0.8em] \text{II} & & \wedge \quad 0 &= 4a + 2b + c \\[0.8em] \text{III} & & \wedge \quad 5 &= c \\[2.4em] \text{I} + \text{II} & & 0 &= 8a + 10 & &| -10 \\[0.8em] & & -10 &= 8a & &| : 8 \\[0.8em] & & a &= -1{,}25 \\[2.4em] a \; \text{in I} & & 0 &= 4 \cdot (-1{,}25) - 2b + 5 \\[0.8em] & & 0 &= -2b \\[0.8em] & & b &= 0 \end{align*}\]
\[\Longrightarrow \quad p(x) = -1{,}25x^2 + 5 \,; \quad D_p = \mathbb R\]

