- Details
- Kategorie: Geometrie 1
In einem kartesischen Koordinatensystem sind die Punkte \(A(0|0|1)\), \(B(2|6|1)\), \(C(-4|8|5)\) und \(D(-6|2|5)\) gegeben. Sie liegen in einer Ebene \(E\) und bilden ein Viereck \(ABCD\), dessen Diagonalen sich im Punkt \(M\) schneiden.
Begründen Sie, dass die Gerade \(AB\) parallel zur \(x_{1}x_{2}\)-Ebene verläuft.
(1 BE)
- Details
- Kategorie: Geometrie 1
Weisen Sie nach, dass das Viereck \(ABCD\) ein Rechteck ist. Bestimmen Sie die Koordinaten von \(M\).
(4 BE)
- Details
- Kategorie: Geometrie 1
Ermitteln Sie eine Gleichung der Ebene \(E\) in Normalenform.
(mögliches Ergebnis: \(E \colon 3x_{1} - x_{2} + 5x_{3} - 5 = 0\))
(3 BE)
- Details
- Kategorie: Geometrie 1
Ein Solarmodul wird an einem Metallrohr befestigt, das auf einer horizontalen Fläche senkrecht steht. Das Solarmodul wird modellhaft durch das Rechteck \(ABCD\) dargestellt. Das Metallrohr lässt sich durch eine Strecke, der Befestigungspunkt am Solarmodul durch den Punkt \(M\) beschreiben (vgl. Abbildung). Die horizontale Fläche liegt im Modell in der \(x_{1}x_{2}\)-Ebene des Koordinatensystems; eine Längeneinheit entspricht 0,8 m in der Realität.
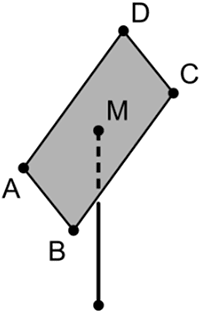
Um einen möglichst großen Energieertrag zu erzielen, sollte die Größe des Neigungswinkels \(\varphi\) des Solarmoduls gegenüber der Horizontalen zwischen 30° und 36° liegen. Prüfen Sie, ob diese Bedingung erfüllt ist.
(3 BE)
- Details
- Kategorie: Geometrie 1
Auf das Solarmodul fällt Sonnenlicht, das im Modell durch parallele Geraden dargestellt wird, die senkrecht zur Ebene \(E\) verlaufen. Das Solarmodul erzeugt auf der horizontalen Fläche einen rechteckigen Schatten. Zeigen Sie unter Verwendung einer geeignet beschrifteten Skizze, dass der Flächeninhalt des Schattens mithilfe des Terms \(\vert \overrightarrow{AB} \vert \cdot \frac{\vert \overrightarrow{AD} \vert}{\cos{\varphi}} \cdot (0{,}8\,\sf{m})^{2}\) berechnet werden kann.
(5 BE)
- Details
- Kategorie: Geometrie 1
Um die Sonneneinstrahlung im Laufe des Tages möglichst effektiv zur Energiegewinnung nutzen zu können, lässt sich das Metallrohr mit dem Solarmodul um die Längsachse des Rohrs drehen. Die Größe des Neigungswinkels \(\varphi\) gegenüber der Horizontalen bleibt dabei unverändert. Betrachtet wird der Eckpunkt des Solarmoduls, der im Modell durch den Punkt \(A\) dargestellt wird. Berechnen Sie den Radius des Kreises, auf dem sich dieser Eckpunkt des Solarmoduls bei der Drehung des Metallrohrs bewegt, auf Zentimeter genau.
(4 BE)

