Weisen Sie nach, dass das Viereck \(ABCD\) ein Rechteck ist. Bestimmen Sie die Koordinaten von \(M\).
(4 BE)
Teilaufgabe b
Lösung zu Teilaufgabe b
Betrag eines Vektors, Orthogonalität zweier Vektoren, Mittelpunkt einer Strecke
Nachweis, dass das Viereck ABCD ein Rechteck ist
Eigenschaften eines Rechtecks:
- Je zwei gegenüberliegende Seiten sind gleich lang. Diese Eigenschaft gilt auch für ein Parallelogramm.
- Alle Innenwinkel betragen 90°. Diese Eigenschaft gilt auch für ein Quadrat.
- Die Diagonalen \(e\) und \(f\) sind gleich lang und schneiden sich nicht rechtwinklig im Mittelpunkt \(M\) der Diagonalen.
1. Möglichkeit: Zwei Seiten und einen Innenwinkel überprüfen
Planskizze: Das Viereck \(ABCD\) ist ein Rechteck, wenn zwei gegenüberliegende Seiten gleich lang und parallel sind, und außerdem zwei anliegende Seiten einen rechten Winkel einschließen.
Beispielsweise ist zu überprüfen: \(\overline{AD} = \overline{BC}; \; [AD] \parallel [BC]\) sowie \(\overrightarrow{AD} \perp \overrightarrow{AB}\)
Verbindungsvektoren \(\overrightarrow{AD}\), \(\overrightarrow{BC}\) und \(\overrightarrow{AB}\) bestimmen:
\(A(0|0|1)\), \(B(2|6|1)\), \(C(-4|8|5)\), \(D(-6|2|5)\)
\[\overrightarrow{AD} = \overrightarrow{D} - \overrightarrow{A} = \begin{pmatrix} -6 \\ 2 \\ 5 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -6 \\ 2 \\ 4 \end{pmatrix}\]
\[\overrightarrow{BC} = \overrightarrow{C} - \overrightarrow{B} = \begin{pmatrix} -4 \\ 8 \\ 5 \end{pmatrix} - \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix} = \begin{pmatrix} -6 \\ 2 \\ 4 \end{pmatrix}\]
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 \\ 6 \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{AD} = \overrightarrow{BC} \quad \Longrightarrow \quad \overline{AD} = \overline{BC}; \; [AD] \parallel [BC]\]
Orthogonalität der Seiten \([AD]\) und \([AB]\) nachweisen:
Die Seiten \([AD]\) und \([AB]\) sind zueinander senkrecht, wenn das Skalarprodukt der Vektoren \(\overrightarrow{AD}\) und \(\overrightarrow{AB}\) gleich Null ist.
\[\overrightarrow{AD} \perp \overrightarrow{AB} \quad \Longleftrightarrow \quad \overrightarrow{AD} \circ \overrightarrow{AB} = 0\]
\[\begin{align*} \overline{AD} \circ \overline{AB} &= \begin{pmatrix} -6 \\ 2 \\ 4 \end{pmatrix} \circ \begin{pmatrix} 2 \\ 6 \\ 0 \end{pmatrix} \\[0.8em] &= (-6) \cdot 2 + 2 \cdot 6 + 4 \cdot 0 \\[0.8em] &= -6 + 6 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{AD} \perp \overrightarrow{AB} \quad \Longrightarrow \quad [AD] \perp [AB]\]
Schlussfolgerung:
Das Viereck \(ABCD\) ist ein Rechteck.
2. Möglichkeit: Diagonalen überprüfen
![Planskizze: Viereck ABCD, Diagonalen [AC] und [BD], Schnittwinkel der Diagonalen](/images/stories/B2017_PT_B_G_1/B2017_PT_B_G_1_b_2.png "Planskizze: Viereck ABCD, Diagonalen [AC] und [BD], Schnittwinkel der Diagonalen")
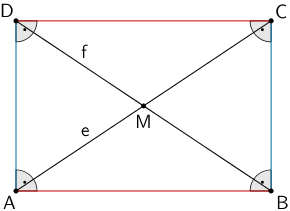
Planskizze: Das Viereck \(ABCD\) ist ein Rechteck, wenn die Diagonalen \([AC]\) und \([BD]\) gleich lang sind.
Zu überprüfen: \(\overline{AC} = \overline{BD}\)
Verbindungsvektoren \(\overrightarrow{AC}\) und \(\overrightarrow{BD}\) bestimmen:
\(A(0|0|1)\), \(B(2|6|1)\), \(C(-4|8|5)\), \(D(-6|2|5)\)
\[\overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} = \begin{pmatrix} -4 \\ 8 \\ 5 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -4 \\ 8 \\ 4 \end{pmatrix}\]
\[\overrightarrow{BD} = \overrightarrow{D} - \overrightarrow{B} = \begin{pmatrix} -6 \\ 2 \\ 5 \end{pmatrix} - \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix} = \begin{pmatrix} -8 \\ -4 \\ 4 \end{pmatrix}\]
Längen der Diagonalen \([AC]\) und \([BD]\) überprüfen:
\[\begin{align*}\overline{AC} &= \vert \overrightarrow{AC} \vert \\[0.8em] &= \left| \begin{pmatrix} -4 \\ 8 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-4)^{2} + 8^{2} + 4^{2}} \\[0.8em] &= \sqrt{96} \\[0.8em] &= 4\sqrt{6}\end{align*}\]
\[\begin{align*}\overline{BD} &= \vert \overrightarrow{AC} \vert \\[0.8em] &= \left| \begin{pmatrix} -8 \\ -4 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-8)^{2} + (-4)^{2} + 4^{2}} \\[0.8em] &= \sqrt{96} \\[0.8em] &= 4\sqrt{6}\end{align*}\]
\[\Longrightarrow \quad \overline{AC} = \overline{BD}\]
Schlussfolgerung:
Das Viereck \(ABCD\) ist ein Rechteck.
Anmerkung:
Die beiden vorgestellten Möglichkeiten für den Nachweis, dass ein Viereck \(ABCD\) ein Rechteck ist, schließen ein Quadrat als Sonderfall eines Rechtecks mit ein.
Soll ausdrücklich nachgewiesen werden, dass ein Viereck \(ABCD\) ein Quadrat ist, sind folgende Zusatzbedingungen zu überprüfen:
- Ungleiche Länge zweier anliegender Seiten bzw.
- sich rechtwinklig schneidende Diagonalen.
Koordinaten des Schnittpunkts \(M\) der Diagonalen des Vierecks \(ABCD\)
\(A(0|0|1)\), \(B(2|6|1)\), \(C(-4|8|5)\), \(D(-6|2|5)\)
Es wird die Diagonale \([AC]\) oder \([BD]\) betrachtet:
\[\begin{align*}\overrightarrow{M} &= \frac{1}{2} \cdot (\overrightarrow{A} + \overrightarrow{C}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \begin{pmatrix} -4 \\ 8 \\ 5 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} -4 \\ 8 \\ 6 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} \end{align*}\]
\[\begin{align*}\overrightarrow{M} &= \frac{1}{2} \cdot (\overrightarrow{B} + \overrightarrow{D}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 2 \\ 6 \\ 1 \end{pmatrix} + \begin{pmatrix} -6 \\ 2 \\ 5 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} -4 \\ 8 \\ 6 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} \end{align*}\]
