Beim Übergang zwischen den beiden Abschnitten des Bohrkanals muss die Bohrrichtung um den Winkel geändert werden, der im Modell durch den Schnittwinkel der beiden Geraden \(AP\) und \(PQ\) beschrieben wird. Bestimmen Sie die Größe dieses Winkels.
(3 BE)
Lösung zu Teilaufgabe b
Die Größe des Schnittwinkels der Geraden \(AP\) und \(PQ\) entspricht der Größe des Winkels \(\varphi\) zwischen den Verbindungsvektoren \(\overrightarrow{AP}\) und \(\overrightarrow{PQ}\).
Anwendung des Skalarprodukts:
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
\[\cos \varphi = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert}\,; \quad \varphi \in [0;\pi]\]
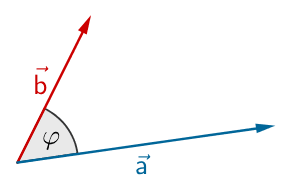
\(\overrightarrow{AP} = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}\); \( \overrightarrow{PQ} = \begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix}\); \(\vert \overrightarrow{AP} \vert = 1\); \(\vert \overrightarrow{PQ} \vert = \sqrt{8{,}25}\) (vgl. Teilaufgabe a)
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \cos{\varphi} &= \frac{\overrightarrow{AP} \circ \overrightarrow{PQ}}{\vert \overrightarrow{AP} \vert \cdot \vert \overrightarrow{PQ} \vert} \\[0.8em] &= \frac{\begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} \circ\begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix} }{1 \cdot \sqrt{8{,}25}} \\[0.8em] &= \frac{0 \cdot 1 + 0 \cdot 1 + (-1) \cdot (-2{,}5)}{\sqrt{8{,}25}} \\[0.8em] &= \frac{2{,}5}{\sqrt{8{,}25}} &&| \; \text{TR}\; \cos^{-1}(\dots) \\[2.4em] \varphi &= \cos^{-1}\left( \frac{2{,}5}{\sqrt{8{,}25}} \right) \approx 29{,}5^{\circ} \end{align*}\]

