Gegeben ist die Funktion \(f\) mit \(f(x) = \sqrt{x - 2} + 1\) und maximalem Definitionsbereich.
Zeichnen Sie den Graphen von \(f\) im Bereich \(2 \leq x \leq 11\) in ein Koordinatensystem.
(3 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = \sqrt{x - 2} + 1\]
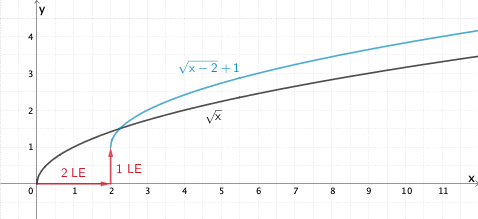
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Der Graph der Funktion \(\textcolor{#0087c1}{f}\) mit \(\textcolor{#0087c1}{f(x) = \sqrt{x \textcolor{#cc071e}{- 2}} \textcolor{#cc071e}{+ 1}}\) ist gegenüber dem Graphen der Funktion \(x \mapsto \sqrt{x}\) um + 2 LE (Längeneinheiten) in x-Richtung und um + 1 LE in y-Richtung verschoben.
(vgl. Abiturskript - Lernhilfen Analysis - Skizzieren der Graphen wichtiger Grundfunktionen)

